www.science.org/doi/10.1126/...

www.science.org/doi/10.1126/...

www.biorxiv.org/content/10.6...

We will lose at least one, if not two generations of knowledge if we don’t get this shit sorted out immediately.
Gutting. How many future scientists have we lost?
We will lose at least one, if not two generations of knowledge if we don’t get this shit sorted out immediately.
🧪🎁🔗 www.nytimes.com/interactive/...

🧪🎁🔗 www.nytimes.com/interactive/...
Einstein sent a letter to Max Born #OTD in 1926, in which he gave his oft-quoted objection to the probabilistic interpretation of the wavefunction in quantum mechanics. 🧪 ⚛️
You may be surprised by where this is headed. (1/n)
Einstein sent a letter to Max Born #OTD in 1926, in which he gave his oft-quoted objection to the probabilistic interpretation of the wavefunction in quantum mechanics. 🧪 ⚛️
You may be surprised by where this is headed. (1/n)



pubs.rsc.org/en/content/a...
pubs.rsc.org/en/content/a...
“Historical and Experimental Evidence that Inherent Properties Are Overweighted in Early Scientific Explanation”
I’m grateful to Zach Horne & my dear advisor @andreicimpian.bsky.social to let me be part of this project, it was a great experience!
doi.org/10.1073/pnas...

“Historical and Experimental Evidence that Inherent Properties Are Overweighted in Early Scientific Explanation”
I’m grateful to Zach Horne & my dear advisor @andreicimpian.bsky.social to let me be part of this project, it was a great experience!
doi.org/10.1073/pnas...
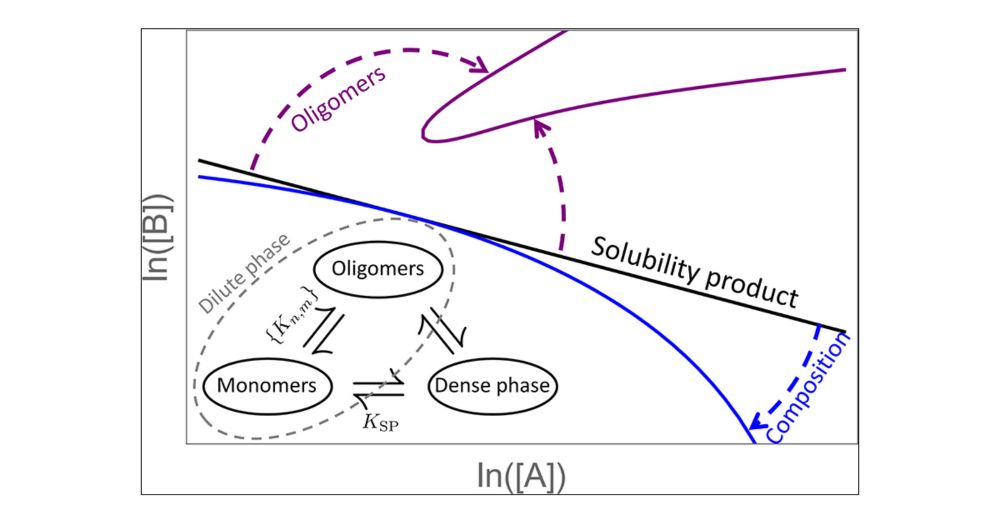
Like palm reading for your phase boundary.
Plus, when is your condensate actually an oligomer (or vice versa)?
A new preprint from the Schmit Group, in collaboration with Jonathon Ditlev, Les Loew, and @ani-chattaraj.bsky.social
www.biorxiv.org/content/10.1...

Like palm reading for your phase boundary.
Plus, when is your condensate actually an oligomer (or vice versa)?
A new preprint from the Schmit Group, in collaboration with Jonathon Ditlev, Les Loew, and @ani-chattaraj.bsky.social
www.biorxiv.org/content/10.1...



