📍SF Bay Area 🔗 http://jonbarron.info
This feed is a mostly-incomplete mirror of https://x.com/jon_barron, I recommend you just follow me there.
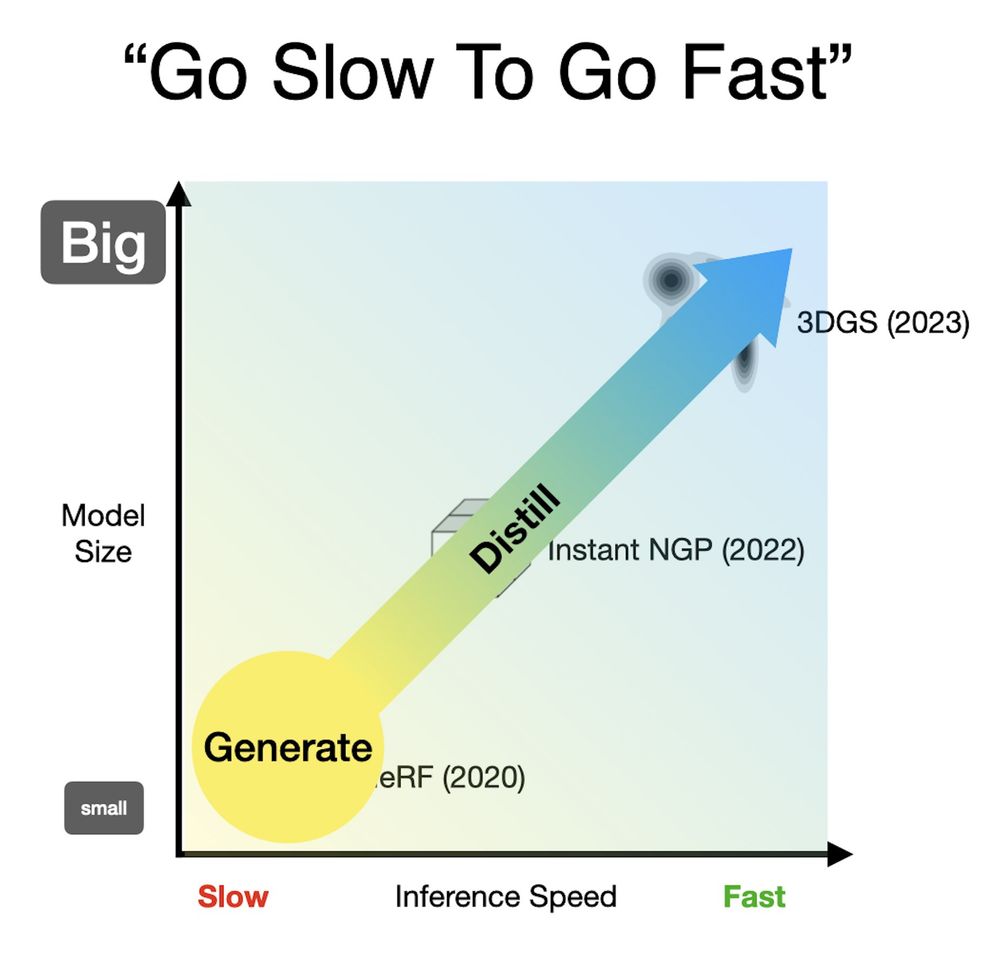
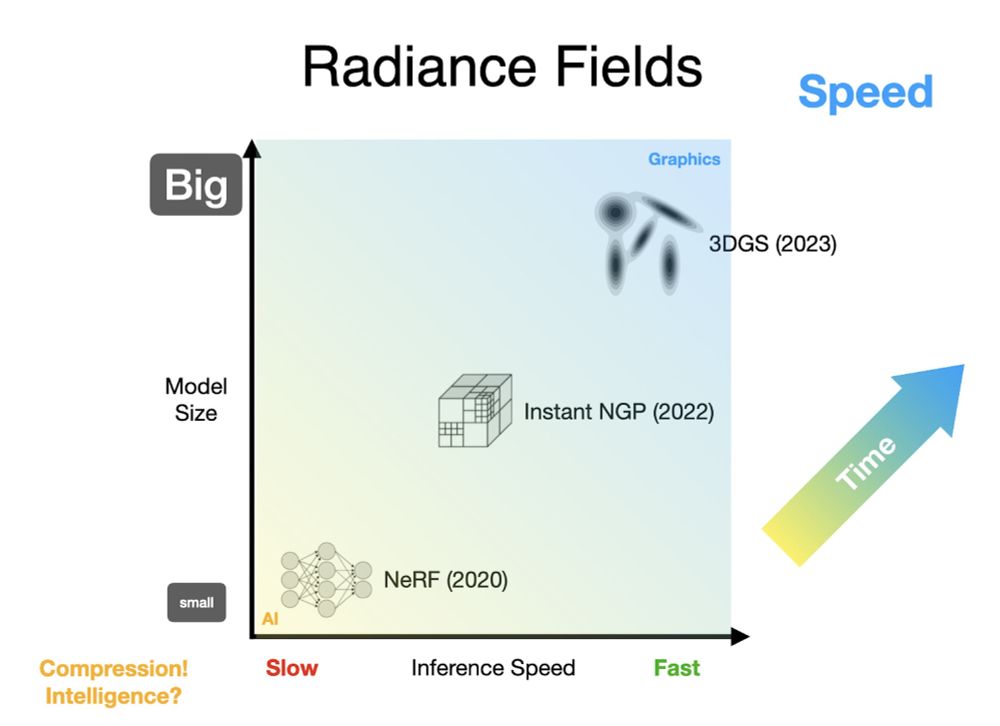
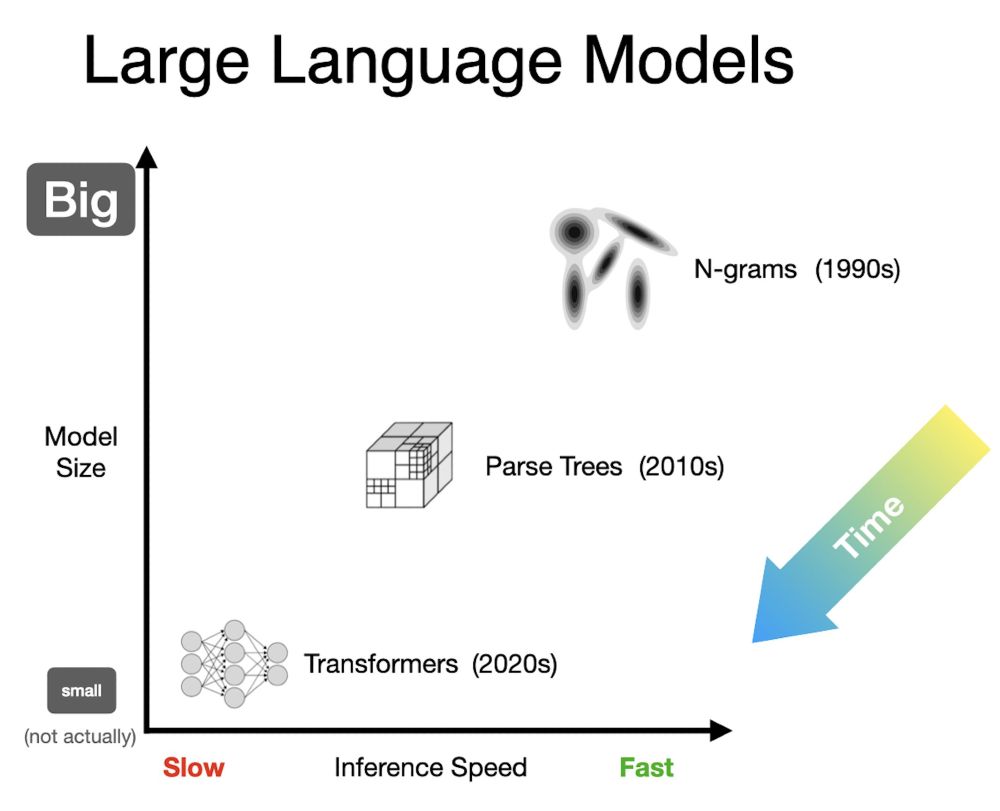
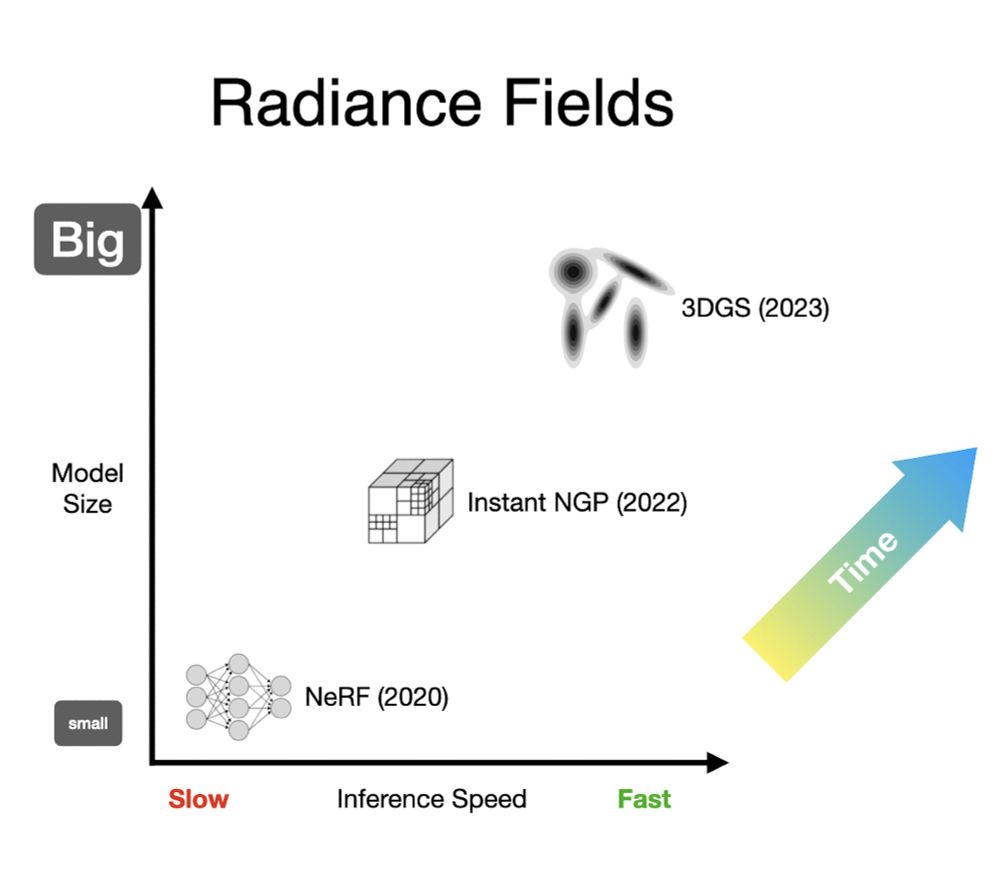


Radiance fields have had 3 distinct generations. First was NeRF: just posenc and a tiny MLP. This was slow to train but worked really well, and it was unusually compressed --- The NeRF was smaller than the images.

Radiance fields have had 3 distinct generations. First was NeRF: just posenc and a tiny MLP. This was slow to train but worked really well, and it was unusually compressed --- The NeRF was smaller than the images.
Project page: szymanowiczs.github.io/bolt3d
Arxiv: arxiv.org/abs/2503.14445
Project page: szymanowiczs.github.io/bolt3d
Arxiv: arxiv.org/abs/2503.14445