Causal Inference 🔴→🟠←🟡.
Machine Learning 🤖🎓.
Data Communication 📈.
Healthcare ⚕️.
Creator of 𝙲𝚊𝚞𝚜𝚊𝚕𝚕𝚒𝚋: https://github.com/IBM/causallib
Website: https://ehud.co



full code: gist.github.com/ehudkr/a9dd3...
![Code snippet for bootstrapping an IPW model, once using only confounding variables, and once using both confounding and prognostic variables.
Code:
```python
n_bootstrap = 1000
res_conf, res_prog = [], []
for i in range(n_bootstrap):
cur_df = df.sample(n=df.shape[0], replace=True, random_state=i)
ipw = IPW(LogisticRegression(penalty=None))
a = cur_df["a"]
y = cur_df["y"]
X = cur_df[["x_conf"]]
ipw.fit(X, a)
po = ipw.estimate_population_outcome(X, a, y)
ate = po[1] - po[0]
res_conf.append(ate)
X = cur_df[["x_conf", "x_prog"]]
ipw.fit(X, a)
po = ipw.estimate_population_outcome(X, a, y)
ate = po[1] - po[0]
res_prog.append(ate)
```](https://cdn.bsky.app/img/feed_thumbnail/plain/did:plc:7ututi7lzr4dqgd675dg2lev/bafkreidvbjjwiyohidhrnkq5fnv3yynfo5tyrr4rqiq3ehg563ix6s7ulm@jpeg)

full code: gist.github.com/ehudkr/a9dd3...
![A screenshot of a code snippet in Python:
```
m = smf.ols("y ~ 1 + x1 + x2", data=df).fit()
n_draws = 100
coefs = rng.multivariate_normal(
mean=m.params, cov=m.cov_params(),
size=n_draws,
)
XX = df.assign(Intercept=1)[["Intercept", "x1", "x2"]]
yy_pred = XX @ coefs.T
```](https://cdn.bsky.app/img/feed_thumbnail/plain/did:plc:7ututi7lzr4dqgd675dg2lev/bafkreiehf6jtlolb3oygwfpdhumk2mkyfk3z3rtaur6k7fc4vgnloohc3y@jpeg)




post ~ pre + X0 + A0 + X1 + A1
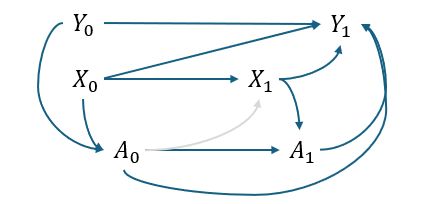
post ~ pre + X0 + A0 + X1 + A1
In the simplest case, if the second treatment is completely randomized then it isn't a big deal:
post ~ pre + X0 + A0 + A1
will suffice

In the simplest case, if the second treatment is completely randomized then it isn't a big deal:
post ~ pre + X0 + A0 + A1
will suffice
The simplest answers will be to ignore treatment being dynamic. It will answer whether treatment _initiation_ is effective, regardless of how patients stick to protocol.

The simplest answers will be to ignore treatment being dynamic. It will answer whether treatment _initiation_ is effective, regardless of how patients stick to protocol.

arxiv.org/abs/2407.12220

arxiv.org/abs/2407.12220
On the left, you don't expect ɛ (y=f(X)+ɛ) to be consistent across data splits since it's random, and thus fitting it is bad.
On the right, you don't expect U (ruler) to appear on deployment, so a model using it instead of X (skin) will be wrong.
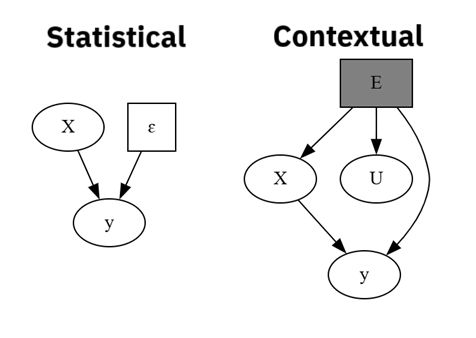
On the left, you don't expect ɛ (y=f(X)+ɛ) to be consistent across data splits since it's random, and thus fitting it is bad.
On the right, you don't expect U (ruler) to appear on deployment, so a model using it instead of X (skin) will be wrong.
I just think overfitting assumes iid train/test, so I'm not sure if cases like described in this paragraph hold (e.g., black swan).
I don't think that poor performance from distribution shift would be classified as "overfitting".

I just think overfitting assumes iid train/test, so I'm not sure if cases like described in this paragraph hold (e.g., black swan).
I don't think that poor performance from distribution shift would be classified as "overfitting".
projecteuclid.org/journals/bay...

projecteuclid.org/journals/bay...


anyways, it's here now, and I'm glad I set down and wrote it because I discovered I had to iron out some personal misunderstandings.
so without further ado and with even shinier visuals, a post about double cross-fitting for #causalinference
ehud.co/blog/2024/03...

anyways, it's here now, and I'm glad I set down and wrote it because I discovered I had to iron out some personal misunderstandings.
so without further ado and with even shinier visuals, a post about double cross-fitting for #causalinference
ehud.co/blog/2024/03...




