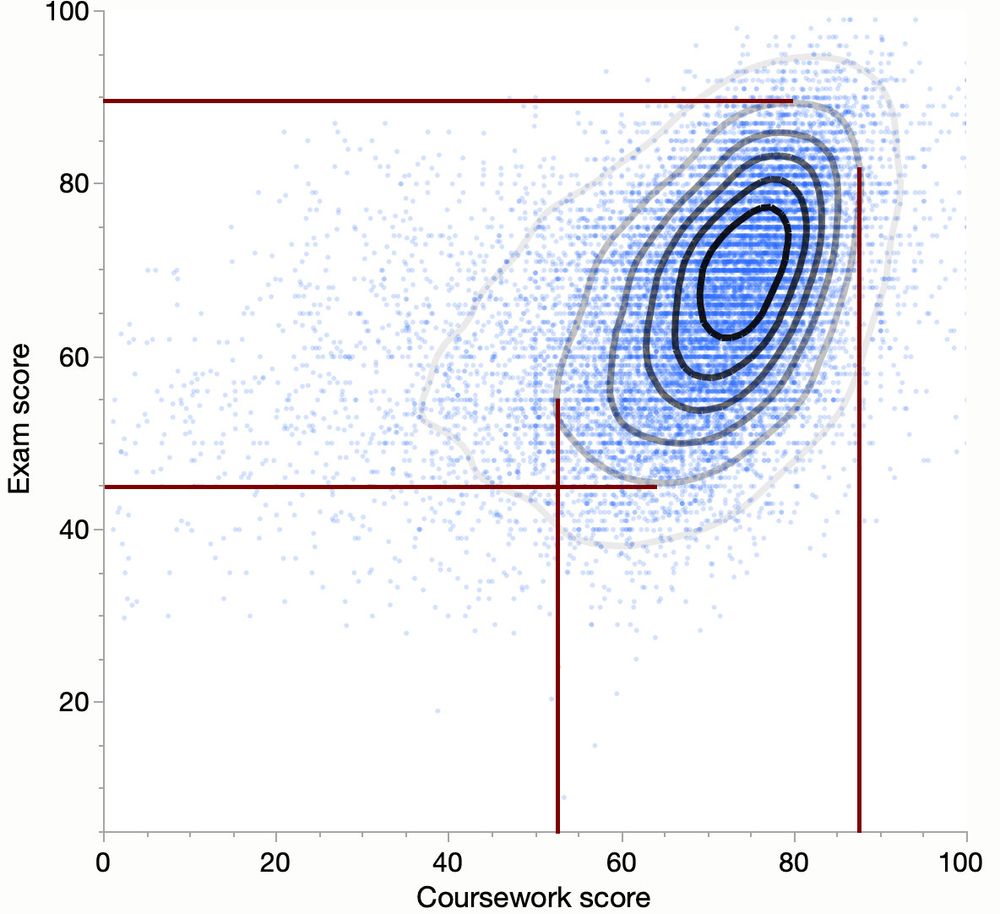
KDE uses a quite large bandwidth (constant or not) to calculate each value "contribution" to the density shape.
My method finds the smoothest density shape assuming each value was measured within a given tolerance.
KDE uses a quite large bandwidth (constant or not) to calculate each value "contribution" to the density shape.
My method finds the smoothest density shape assuming each value was measured within a given tolerance.