Classical PAV: monotone but step-flattened.
TPM: monotone and trend-faithful, maintaining readable dynamics such as endpoints, mass, slope continuity, inflection timing, and relative growth/decay patterns.

Classical PAV: monotone but step-flattened.
TPM: monotone and trend-faithful, maintaining readable dynamics such as endpoints, mass, slope continuity, inflection timing, and relative growth/decay patterns.




I decided to reinterpret the same data without using the time connected scatterplot designed by Max Roser ourworldindata.org/us-life-expe....


I decided to reinterpret the same data without using the time connected scatterplot designed by Max Roser ourworldindata.org/us-life-expe....
Main idea, several perspectives (different contexts) of the same world (of 100 people).

Main idea, several perspectives (different contexts) of the same world (of 100 people).
If is possible to trade some vertical space (or dot size) the overlapping can be improved even further.


If is possible to trade some vertical space (or dot size) the overlapping can be improved even further.
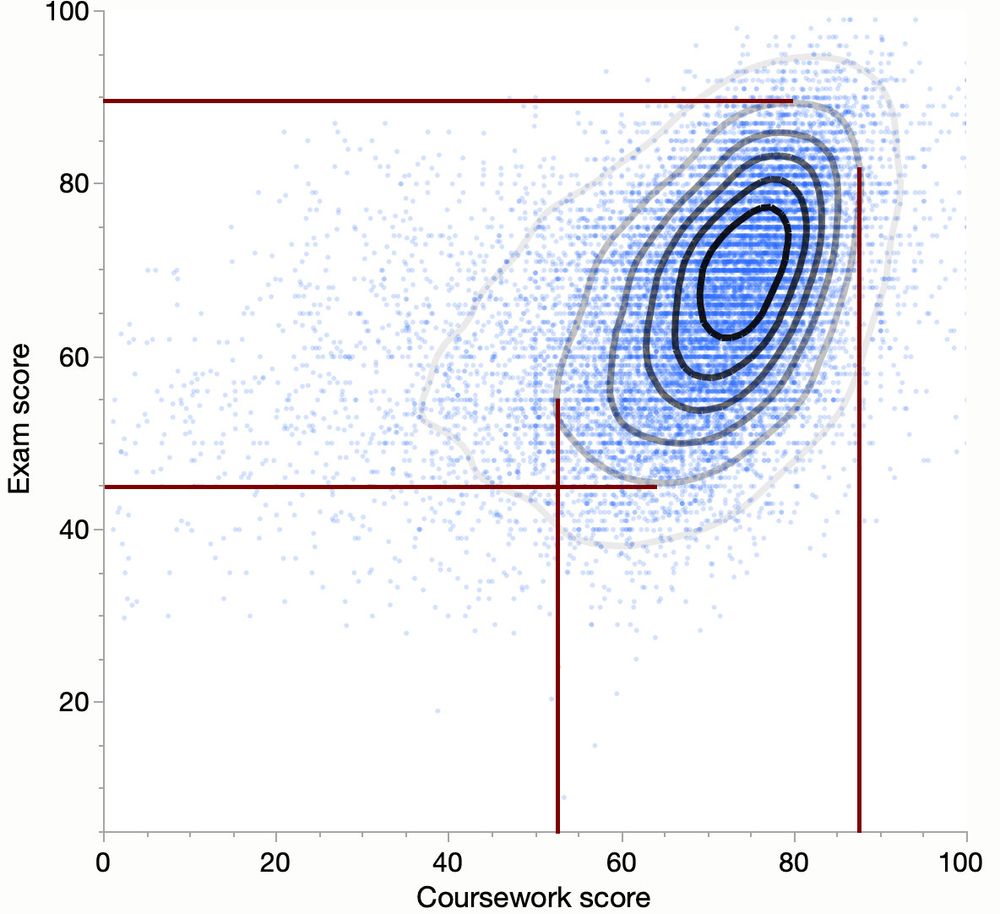
Attached another arrangement (same dot size and space), with precise encoding of both the distribution shape and the dots position, without noticeable visual patterns/artifacts.

Attached another arrangement (same dot size and space), with precise encoding of both the distribution shape and the dots position, without noticeable visual patterns/artifacts.
The tradeoff? See below.

The tradeoff? See below.
One technique I've suggested in the past is a heatmap/line chart combo, which, besides individual decoding improvement, it also makes the scale distinction clear and it guards against magnitude comparison.
(see the attached sequence)




One technique I've suggested in the past is a heatmap/line chart combo, which, besides individual decoding improvement, it also makes the scale distinction clear and it guards against magnitude comparison.
(see the attached sequence)


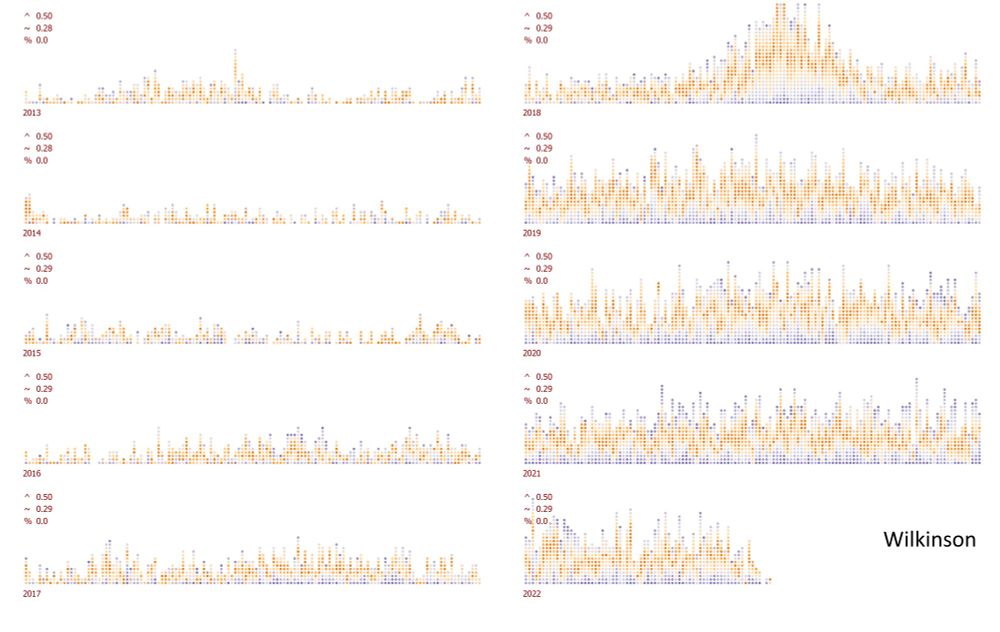
A seriously vertically squeezed Wilkinson dot plot (unit histogram) for comparison (the dot piles are much higher).

A seriously vertically squeezed Wilkinson dot plot (unit histogram) for comparison (the dot piles are much higher).
A bridge between the descriptive and inferential aspects of distributions, a quantile and a density estimator.

A bridge between the descriptive and inferential aspects of distributions, a quantile and a density estimator.

(matching the Winkinson dots plot precision of 0.5x dot size)

(matching the Winkinson dots plot precision of 0.5x dot size)


(attached a max one dot size placement error on an hex-layout)

(attached a max one dot size placement error on an hex-layout)
Read Leland Wilkinson's reply to Beeswarm Plot article (www.r-statistics.com/2011/03/bees...).

Read Leland Wilkinson's reply to Beeswarm Plot article (www.r-statistics.com/2011/03/bees...).