
benspitz.com

The image below shows how you can use the package to compute a free resolution of a C_p-Mackey functor.
The image below shows how you can use the package to compute a free resolution of a C_p-Mackey functor.

The image below shows how you can use the package to compute a free resolution of a C_p-Mackey functor.

Let f ∈ ℂ[x] be a polynomial of degree ≥2. Let z ∈ ℂ. Must there exist a critical point w of f such that
|(f(z)-f(w))/(z-w)| ≤ |f'(z)|?
Let f ∈ ℂ[x] be a polynomial of degree ≥2. Let z ∈ ℂ. Must there exist a critical point w of f such that
|(f(z)-f(w))/(z-w)| ≤ |f'(z)|?
Does there exist a finite (simple, undirected) graph which has diameter 2, girth* 5, and is 57-regular?
* The girth of a graph G is the smallest length of a cycle in G.
Does there exist a finite (simple, undirected) graph which has diameter 2, girth* 5, and is 57-regular?
* The girth of a graph G is the smallest length of a cycle in G.
Recall that the totient function ϕ is defined by sending each positive integer n to the number of positive integers k ≤ n which are coprime to n.
Conjecture. For all positive integers x, there exists a positive integer y≠x such that ϕ(x)=ϕ(y)
Recall that the totient function ϕ is defined by sending each positive integer n to the number of positive integers k ≤ n which are coprime to n.
Conjecture. For all positive integers x, there exists a positive integer y≠x such that ϕ(x)=ϕ(y)
Let L be a finite lattice (i.e. a nonempty finite poset such that any two elements have both an inf and a sup).
Must there exist a finite group G with subgroups H, K such that L is isomorphic to the poset
{X ≤ G : H ≤ X ≤ K}
ordered by ⊆?
Let L be a finite lattice (i.e. a nonempty finite poset such that any two elements have both an inf and a sup).
Must there exist a finite group G with subgroups H, K such that L is isomorphic to the poset
{X ≤ G : H ≤ X ≤ K}
ordered by ⊆?
Let f : ℕ → ℕ be a bijection.
Must there exist a natural number n and a positive integer k such that either
f(n) > f(n+k) > f(n+2k) > f(n+3k)
or
f(n) < f(n+k) < f(n+2k) < f(n+3k)?
Let f : ℕ → ℕ be a bijection.
Must there exist a natural number n and a positive integer k such that either
f(n) > f(n+k) > f(n+2k) > f(n+3k)
or
f(n) < f(n+k) < f(n+2k) < f(n+3k)?
Let n be a positive integer. Let f : ℂⁿ → ℂⁿ be a regular* function such that the determinant of its Jacobian matrix is a nonzero constant.
Must f be bijective with regular inverse?
*i.e. each component ℂⁿ → ℂ is a polynomial
Let n be a positive integer. Let f : ℂⁿ → ℂⁿ be a regular* function such that the determinant of its Jacobian matrix is a nonzero constant.
Must f be bijective with regular inverse?
*i.e. each component ℂⁿ → ℂ is a polynomial
Conjecture (Poonen): 100% (asymptotic density) of finite commutative rings have characteristic EXACTLY 8, i.e. 4 ≠ 0 and 8 = 0 both hold.
From this amazing paper: arxiv.org/abs/math/060...

Conjecture (Poonen): 100% (asymptotic density) of finite commutative rings have characteristic EXACTLY 8, i.e. 4 ≠ 0 and 8 = 0 both hold.
From this amazing paper: arxiv.org/abs/math/060...
Conjecture (Rota). Let n be a natural number. Let V be an n-dimensional vector space. Let B₁, …, Bₙ be bases of V.
Then there exist orderings of these bases
Bₖ = (bₖ₁, …, bₖₙ)
such that {b₁ₖ, …, bₙₖ} is a basis of V for all 1 ≤ k ≤ n.
Conjecture (Rota). Let n be a natural number. Let V be an n-dimensional vector space. Let B₁, …, Bₙ be bases of V.
Then there exist orderings of these bases
Bₖ = (bₖ₁, …, bₖₙ)
such that {b₁ₖ, …, bₙₖ} is a basis of V for all 1 ≤ k ≤ n.
Conjecture (Frankl). Let X be a finite set, and let S ⊆ P(X) be a collection of subsets of X which is closed under union.
If S≠∅ and S≠{∅}, then some element x∈X appears in at least half of the elements of S, i.e.
2|{s ∈ S : x ∈ s}| ≥ |S|.
Conjecture (Frankl). Let X be a finite set, and let S ⊆ P(X) be a collection of subsets of X which is closed under union.
If S≠∅ and S≠{∅}, then some element x∈X appears in at least half of the elements of S, i.e.
2|{s ∈ S : x ∈ s}| ≥ |S|.
Must there exist a vector x ∈ Fⁿ such that neither x nor Ax has 0 as one of its entries?
~ spoilers below ~
Must there exist a vector x ∈ Fⁿ such that neither x nor Ax has 0 as one of its entries?
~ spoilers below ~
arxiv.org/abs/2507.14068
arxiv.org/abs/2507.14068
In this paper, we also get to take a limit as p (a prime) approaches 1 :^)

In this paper, we also get to take a limit as p (a prime) approaches 1 :^)
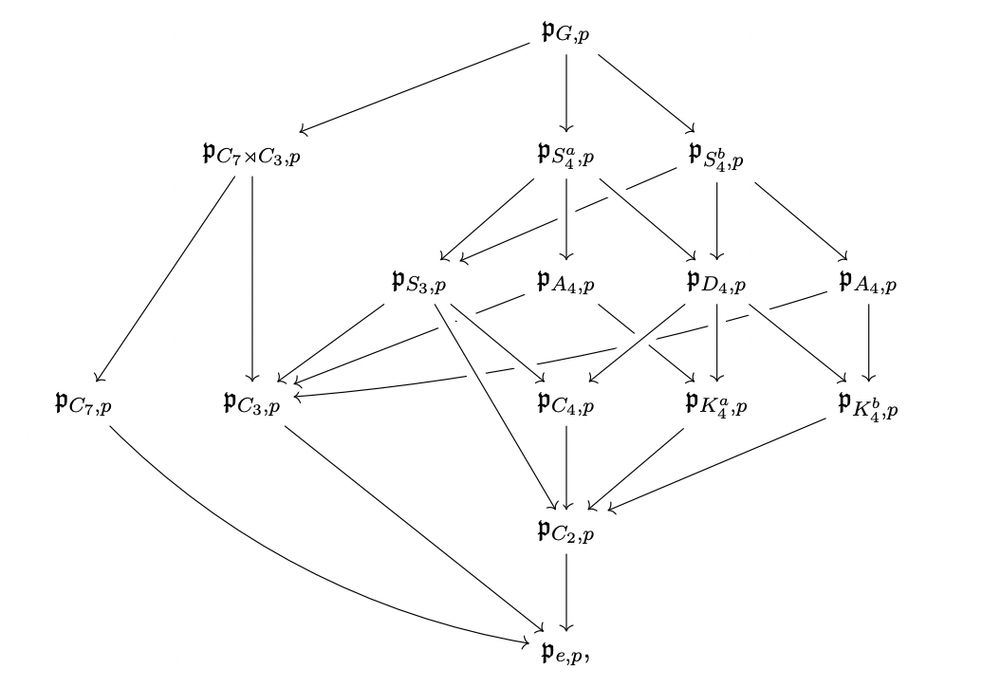
Maxine and Sam Ginnett worked out this story for cyclic groups a few years ago, and together we realized that the ideas from our ghost paper this October might allow us to push the argument through for all finite groups.
"Might" turned out to be "do" :)
arxiv.org/abs/2506.10727

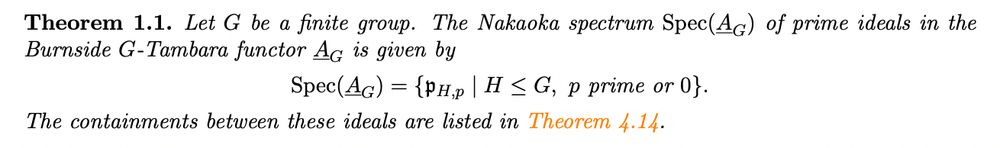
Maxine and Sam Ginnett worked out this story for cyclic groups a few years ago, and together we realized that the ideas from our ghost paper this October might allow us to push the argument through for all finite groups.
"Might" turned out to be "do" :)
Title: "Algebraically Closed Tambara Functors"
youtu.be/ast_KRMwBOQ?...
Title: "Algebraically Closed Tambara Functors"
youtu.be/ast_KRMwBOQ?...

Conversely, if your hearing is such that you can understand everyone, it is called cochlear
Conversely, if your hearing is such that you can understand everyone, it is called cochlear
Feat. Talon on guitar, me on piano, Rohan Joshi on the board, and a great crowd of friends on vocals :)
youtu.be/xanZ3tAkhRo

Feat. Talon on guitar, me on piano, Rohan Joshi on the board, and a great crowd of friends on vocals :)
youtu.be/xanZ3tAkhRo
youtu.be/KvYYpJARP6M

youtu.be/KvYYpJARP6M
My intention was to make the exposition accessible to ~any math grad student; take a look if you're interested!
youtu.be/H5PsXY0E7Bw

My intention was to make the exposition accessible to ~any math grad student; take a look if you're interested!
youtu.be/H5PsXY0E7Bw


