If you take any f : {-1,+1}ⁿ → ℝ⁺ and apply the noise operator T_{.99}, the resulting function g = T_{.99} f satisfies a better-than-Markov inequality. That is, Pr[g > t E[g]] < o(1/t).
If you take any f : {-1,+1}ⁿ → ℝ⁺ and apply the noise operator T_{.99}, the resulting function g = T_{.99} f satisfies a better-than-Markov inequality. That is, Pr[g > t E[g]] < o(1/t).
Or if you prefer a special case, "Subset-Sum with vectors mod 3":
www.youtube.com/watch?v=Pl2b...

Or if you prefer a special case, "Subset-Sum with vectors mod 3":
www.youtube.com/watch?v=Pl2b...

youtu.be/QH4MviUE0_s

youtu.be/QH4MviUE0_s
1995 papers: dblp.org/db/conf/focs...
2005 papers: dblp.org/db/conf/focs...
2015 papers: dblp.org/db/conf/focs...
Nomination instructions here:
tc.computer.org/tcmf/2025/08...
1995 papers: dblp.org/db/conf/focs...
2005 papers: dblp.org/db/conf/focs...
2015 papers: dblp.org/db/conf/focs...
Nomination instructions here:
tc.computer.org/tcmf/2025/08...
www.nsf.gov/news/nsf-inv...

www.nsf.gov/news/nsf-inv...
arxiv.org/abs/2507.11536

arxiv.org/abs/2507.11536
arxiv.org/abs/2507.06010
1/3

arxiv.org/abs/2507.06010
1/3
cs.unibocconi.eu/call-nominat...
(Intent-to-nominate letters due by July 31.)
cs.unibocconi.eu/call-nominat...
(Intent-to-nominate letters due by July 31.)
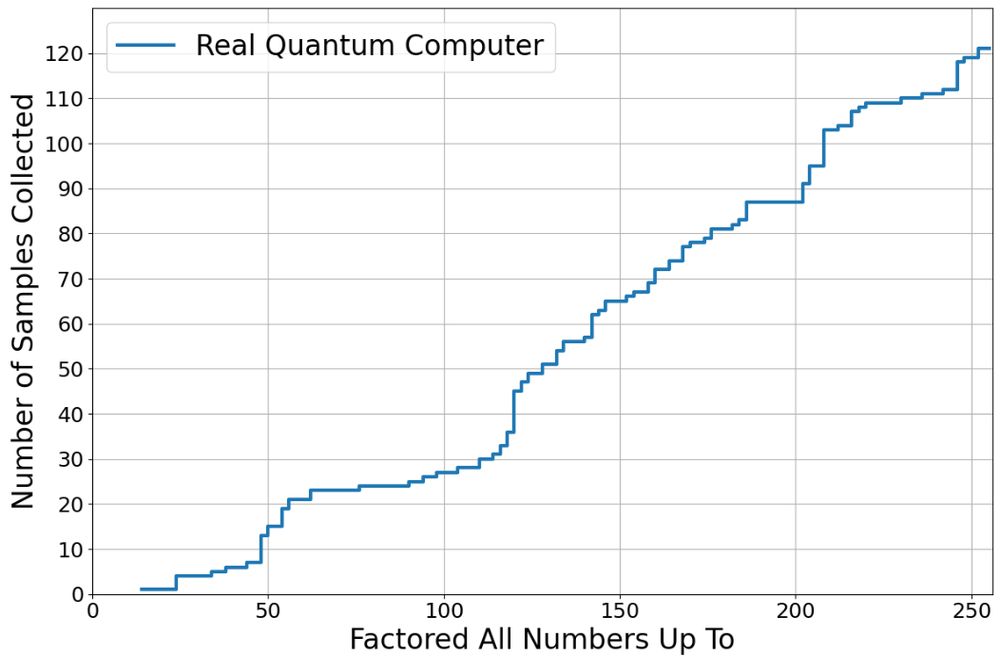
I did it as legit as I possibly could. I ran a correct circuit with no optimization shenanigans. I did correct pre/postprocessing.
It took 121 quantum samples to finish the entire task.
But...
Apply here: stoc2025theoryfest.netlify.app
Apply here: stoc2025theoryfest.netlify.app
people.csail.mit.edu/rrw/time-vs-...
It's still hard for me to believe it myself, but I seem to have shown that TIME[t] is contained in SPACE[sqrt{t log t}].
To appear in STOC. Comments are very welcome!
people.csail.mit.edu/rrw/time-vs-...
It's still hard for me to believe it myself, but I seem to have shown that TIME[t] is contained in SPACE[sqrt{t log t}].
To appear in STOC. Comments are very welcome!
"x1 += x2", "x2 += x3", "x3 += x4",
and versions with "-=" that cancel them.
We define a program
"x1 += x2"
"x2 += x3"
"x1 -= x2"
"x2 -= x3",
and abbreviate it "x1 -= x3". We similarly define "x2 -= x4".
We posit that "x1 -= x3" commutes with [...]
"x1 += x2", "x2 += x3", "x3 += x4",
and versions with "-=" that cancel them.
We define a program
"x1 += x2"
"x2 += x3"
"x1 -= x2"
"x2 -= x3",
and abbreviate it "x1 -= x3". We similarly define "x2 -= x4".
We posit that "x1 -= x3" commutes with [...]
Also define ♕=♀️🏁♀️⁻¹🏁⁻¹ and ♔=♂️🏁♂️⁻¹🏁⁻¹.
We posit:
♀️♕=♕♀️ and 🏁♕=♕🏁 and ♂️♔=♔♂️ and 🏁♔=♔🏁.
And we posit:
♀️²⁰²⁵=🏁²⁰²⁵=♂️²⁰²⁵=1 (identity).
Can you prove ♕♔=♔♕?
Also define ♕=♀️🏁♀️⁻¹🏁⁻¹ and ♔=♂️🏁♂️⁻¹🏁⁻¹.
We posit:
♀️♕=♕♀️ and 🏁♕=♕🏁 and ♂️♔=♔♂️ and 🏁♔=♔🏁.
And we posit:
♀️²⁰²⁵=🏁²⁰²⁵=♂️²⁰²⁵=1 (identity).
Can you prove ♕♔=♔♕?
It's a warmup for the main project...
It's a warmup for the main project...
*more or less all

*more or less all
arxiv.org/pdf/2412.20263 by Jiaoyang Huang, Theo Mckenzie, HT Yau.
In particular, infinitely many 7-regular Ramanujan graphs exist.
arxiv.org/pdf/2412.20263 by Jiaoyang Huang, Theo Mckenzie, HT Yau.
In particular, infinitely many 7-regular Ramanujan graphs exist.
It's kind of about group theory, though.
toc.csail.mit.edu/node/1671
Besides coauthor Noah Singer (@singerng_), here's the cast of characters:

It's kind of about group theory, though.
toc.csail.mit.edu/node/1671
Besides coauthor Noah Singer (@singerng_), here's the cast of characters:
eccc.weizmann.ac.il/report/2024/...
eccc.weizmann.ac.il/report/2024/...
"given a uniformly random vector y of F_q^q, some integers k<q and u < q/2, find a polynomial P(x) of degree <k such that
|P(i)-y_i| < u for all i".
quantum computers can help here (1/4)
"given a uniformly random vector y of F_q^q, some integers k<q and u < q/2, find a polynomial P(x) of degree <k such that
|P(i)-y_i| < u for all i".
quantum computers can help here (1/4)

