
📖 ccanonne.github.io/survey-topic... [Latest draft+exercise solns, free]
📗 nowpublishers.com/article/Deta... [Official pub]
📝 github.com/ccanonne/sur... [LaTeX source]

But now, WHICH FAMILY of bent functions to choose for f?

But now, WHICH FAMILY of bent functions to choose for f?
Key idea: a construction still based on bent functions, but a different type of bent functions we* found.
📝 Have a read! arxiv.org/abs/2602.07503
* Kenny
** (almost)

Key idea: a construction still based on bent functions, but a different type of bent functions we* found.
📝 Have a read! arxiv.org/abs/2602.07503
* Kenny
** (almost)
Now, the eagle-eyed BlueSkyer may notice their lower bound in the extremal regime is 2^(n/4), not 2^(n/2). Bummer! Indeed, their own lower bound construction could only get you so far.. Not a problem with the analysis, the construction itself.

Now, the eagle-eyed BlueSkyer may notice their lower bound in the extremal regime is 2^(n/4), not 2^(n/2). Bummer! Indeed, their own lower bound construction could only get you so far.. Not a problem with the analysis, the construction itself.
Until recently, when Girish and Servdio showed, using a completely different construction based on "bent functions", that yep—it remains hard!

Until recently, when Girish and Servdio showed, using a completely different construction based on "bent functions", that yep—it remains hard!
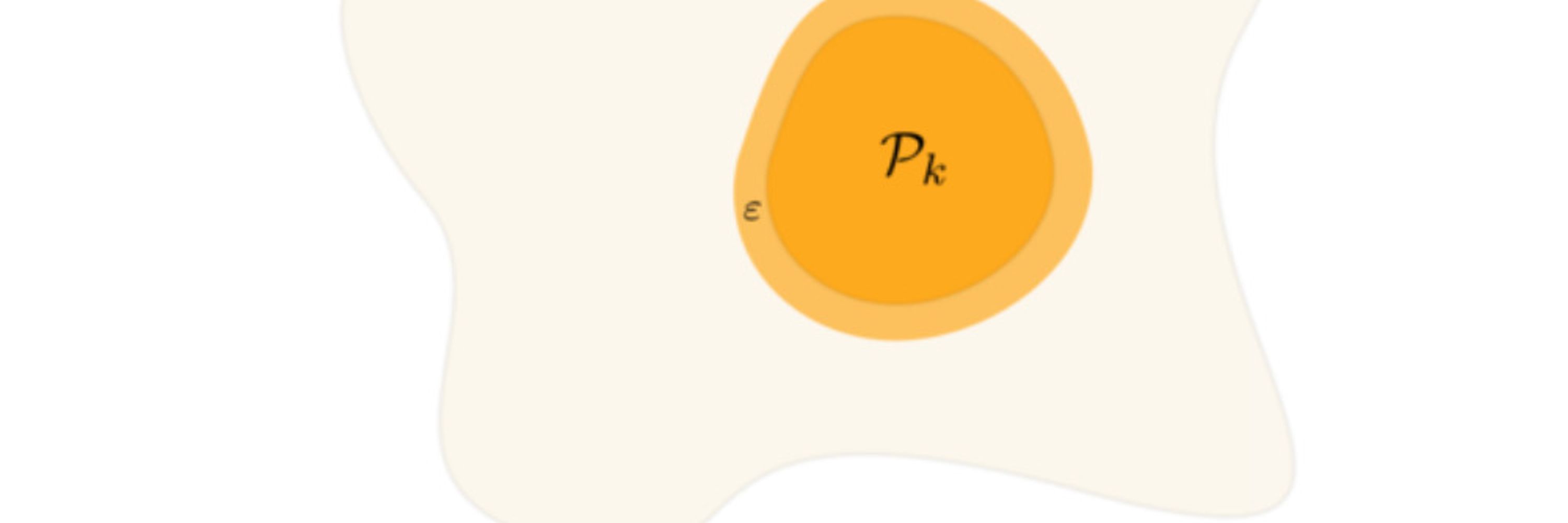
2^(n/2) is a LOT more than 1. But.. ε < 2/π??
2^(n/2) is a LOT more than 1. But.. ε < 2/π??
That's a task easy by design for quantum algos, "because Hadamard": 1 query!

That's a task easy by design for quantum algos, "because Hadamard": 1 query!
📝 arxiv.org/abs/2602.07503
*(in the query model)
📝 arxiv.org/abs/2602.07503
*(in the query model)
🔗 More about SoCG'26: computational-geometry.org/cg-week/socg/
👤 @jgudmundsson.bsky.social
#computationalgeometry #theory #algorithms
🔗 More about SoCG'26: computational-geometry.org/cg-week/socg/
👤 @jgudmundsson.bsky.social
#computationalgeometry #theory #algorithms
It's coffee, not T!
It's coffee, not T!
📝 forms.gle/xrvc2mLRbMqK...
Please spread this! #TCSSky
It's all downhill from here.
It's all downhill from here.
arxiv.org/abs/2602.02744

arxiv.org/abs/2602.02744
📝 forms.gle/xrvc2mLRbMqK...
Please spread this! #TCSSky
📝 forms.gle/xrvc2mLRbMqK...
Please spread this! #TCSSky
(In case you missed it, here's the course: www.gautamkamath.com/CS860-fa2020..., ft full notes & videos)
(In case you missed it, here's the course: www.gautamkamath.com/CS860-fa2020..., ft full notes & videos)
📝 forms.gle/xrvc2mLRbMqK...
Please spread this! #TCSSky
📝 forms.gle/xrvc2mLRbMqK...
Please spread this! #TCSSky
This can be solved with 1 quantum query to the oracles for f,g, but classically exponentially many queries (in n) are known to be necessary for most values of ε... Only the extremal case (eps=1, "as (anti)correlated as possible" was not fully understood.
This can be solved with 1 quantum query to the oracles for f,g, but classically exponentially many queries (in n) are known to be necessary for most values of ε... Only the extremal case (eps=1, "as (anti)correlated as possible" was not fully understood.


