A Erdem Sagtekin
@aesagtekin.bsky.social
theoretical neuroscience phd student at columbia
1/7 How should feedback signals influence a network during learning? Should they first adjust synaptic weights, which then indirectly change neural activity (as in backprop.)? Or should they first adjust neural activity to guide synaptic updates (e.g., target prop.)? openreview.net/forum?id=xVI...
January 8, 2026 at 10:10 PM
1/7 How should feedback signals influence a network during learning? Should they first adjust synaptic weights, which then indirectly change neural activity (as in backprop.)? Or should they first adjust neural activity to guide synaptic updates (e.g., target prop.)? openreview.net/forum?id=xVI...
Reposted by A Erdem Sagtekin
1/X Excited to present this preprint on multi-tasking, with
@david-g-clark.bsky.social and Ashok Litwin-Kumar! Timely too, as “low-D manifold” has been trending again. (If you read thru the end, we escape Flatland and return to the glorious high-D world we deserve.) www.biorxiv.org/content/10.6...
@david-g-clark.bsky.social and Ashok Litwin-Kumar! Timely too, as “low-D manifold” has been trending again. (If you read thru the end, we escape Flatland and return to the glorious high-D world we deserve.) www.biorxiv.org/content/10.6...
A theory of multi-task computation and task selection
Neural activity during the performance of a stereotyped behavioral task is often described as low-dimensional, occupying only a limited region in the space of all firing-rate patterns. This region has...
www.biorxiv.org
December 15, 2025 at 7:41 PM
1/X Excited to present this preprint on multi-tasking, with
@david-g-clark.bsky.social and Ashok Litwin-Kumar! Timely too, as “low-D manifold” has been trending again. (If you read thru the end, we escape Flatland and return to the glorious high-D world we deserve.) www.biorxiv.org/content/10.6...
@david-g-clark.bsky.social and Ashok Litwin-Kumar! Timely too, as “low-D manifold” has been trending again. (If you read thru the end, we escape Flatland and return to the glorious high-D world we deserve.) www.biorxiv.org/content/10.6...
Reposted by A Erdem Sagtekin
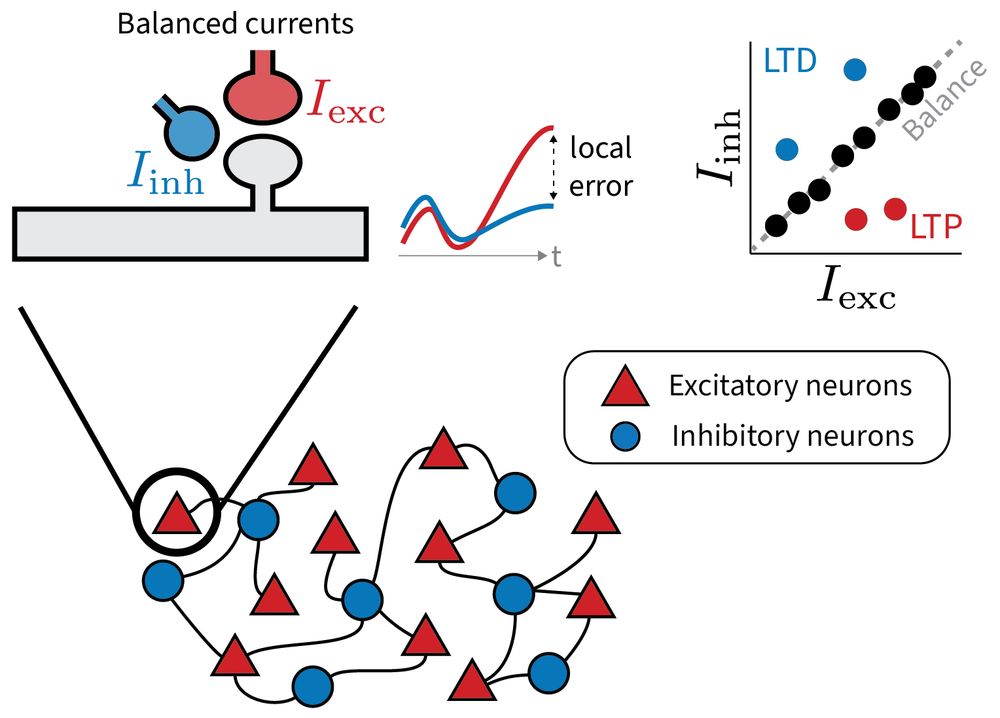
1/6 Why does the brain maintain such precise excitatory-inhibitory balance?
Our new preprint explores a provocative idea: Small, targeted deviations from this balance may serve a purpose: to encode local error signals for learning.
www.biorxiv.org/content/10.1...
led by @jrbch.bsky.social
Our new preprint explores a provocative idea: Small, targeted deviations from this balance may serve a purpose: to encode local error signals for learning.
www.biorxiv.org/content/10.1...
led by @jrbch.bsky.social
May 27, 2025 at 7:49 AM
1/6 Why does the brain maintain such precise excitatory-inhibitory balance?
Our new preprint explores a provocative idea: Small, targeted deviations from this balance may serve a purpose: to encode local error signals for learning.
www.biorxiv.org/content/10.1...
led by @jrbch.bsky.social
Our new preprint explores a provocative idea: Small, targeted deviations from this balance may serve a purpose: to encode local error signals for learning.
www.biorxiv.org/content/10.1...
led by @jrbch.bsky.social
Reposted by A Erdem Sagtekin
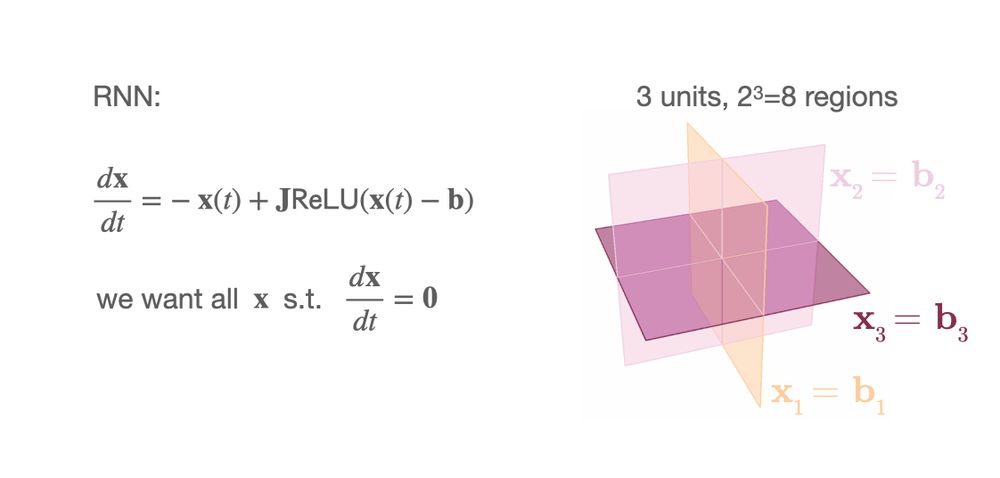
How to find all fixed points in piece-wise linear recurrent neural networks (RNNs)?
A short thread 🧵
In RNNs with N units with ReLU(x-b) activations the phase space is partioned in 2^N regions by hyperplanes at x=b 1/7
A short thread 🧵
In RNNs with N units with ReLU(x-b) activations the phase space is partioned in 2^N regions by hyperplanes at x=b 1/7
December 11, 2024 at 1:32 AM
How to find all fixed points in piece-wise linear recurrent neural networks (RNNs)?
A short thread 🧵
In RNNs with N units with ReLU(x-b) activations the phase space is partioned in 2^N regions by hyperplanes at x=b 1/7
A short thread 🧵
In RNNs with N units with ReLU(x-b) activations the phase space is partioned in 2^N regions by hyperplanes at x=b 1/7
Reposted by A Erdem Sagtekin
(1/5) Fun fact: Several classic results in the stat. mech. of learning can be derived in a couple lines of simple algebra!
In this paper with Haim Sompolinsky, we simplify and unify derivations for high-dimensional convex learning problems using a bipartite cavity method.
arxiv.org/abs/2412.01110
In this paper with Haim Sompolinsky, we simplify and unify derivations for high-dimensional convex learning problems using a bipartite cavity method.
arxiv.org/abs/2412.01110
Simplified derivations for high-dimensional convex learning problems
Statistical physics provides tools for analyzing high-dimensional problems in machine learning and theoretical neuroscience. These calculations, particularly those using the replica method, often invo...
arxiv.org
December 3, 2024 at 7:34 PM
(1/5) Fun fact: Several classic results in the stat. mech. of learning can be derived in a couple lines of simple algebra!
In this paper with Haim Sompolinsky, we simplify and unify derivations for high-dimensional convex learning problems using a bipartite cavity method.
arxiv.org/abs/2412.01110
In this paper with Haim Sompolinsky, we simplify and unify derivations for high-dimensional convex learning problems using a bipartite cavity method.
arxiv.org/abs/2412.01110
This list likely reflects mainly my interests and circle, and I’m sure I’ve missed many people, but I gave it a try: (I’ll be slowly editing it until it reaches 150/150)
go.bsky.app/7VFUkdn
(also, I tried but couldn't remove my profile...)
go.bsky.app/7VFUkdn
(also, I tried but couldn't remove my profile...)
November 9, 2024 at 12:35 PM
This list likely reflects mainly my interests and circle, and I’m sure I’ve missed many people, but I gave it a try: (I’ll be slowly editing it until it reaches 150/150)
go.bsky.app/7VFUkdn
(also, I tried but couldn't remove my profile...)
go.bsky.app/7VFUkdn
(also, I tried but couldn't remove my profile...)
i enjoyed reading the geometry of plasticity paper and felt that something important was coming, this is it:
Check out our new preprint! We show there is a better learning algorithm for #compneuro than gradient descent (GD): exponentiated gradients (EG).
tl;dr: EG respects Dale's law, produces weight distributions that match biology, and outperforms GD in biologically relevant scenarios.
🧠📈 🧪
tl;dr: EG respects Dale's law, produces weight distributions that match biology, and outperforms GD in biologically relevant scenarios.
🧠📈 🧪
Why does #compneuro need new learning methods? ANN models are usually trained with Gradient Descent (GD), which violates biological realities like Dale’s law and log-normal weights. Here we describe a superior learning algorithm for comp neuro: Exponentiated Gradients (EG)! 1/12 #neuroscience 🧪
November 1, 2024 at 8:35 AM
i enjoyed reading the geometry of plasticity paper and felt that something important was coming, this is it: