Paul Hagemann
@yungbayesian.bsky.social
PhD student at TU Berlin, working on generative models and inverse problems
he/him
he/him
Reposted by Paul Hagemann
We are looking for someone to join the group as a postdoc to help us with scaling implicit transfer operators. If you are interested in this, please reach out to me through email. Include CV, with publications and brief motivational statement. RTs appreciated!
May 27, 2025 at 1:23 PM
We are looking for someone to join the group as a postdoc to help us with scaling implicit transfer operators. If you are interested in this, please reach out to me through email. Include CV, with publications and brief motivational statement. RTs appreciated!
Reposted by Paul Hagemann
2025 CHAIR Structured Learning Workshop -- Apply to attend: ui.ungpd.com/Events/60bfc...

May 6, 2025 at 10:02 AM
2025 CHAIR Structured Learning Workshop -- Apply to attend: ui.ungpd.com/Events/60bfc...
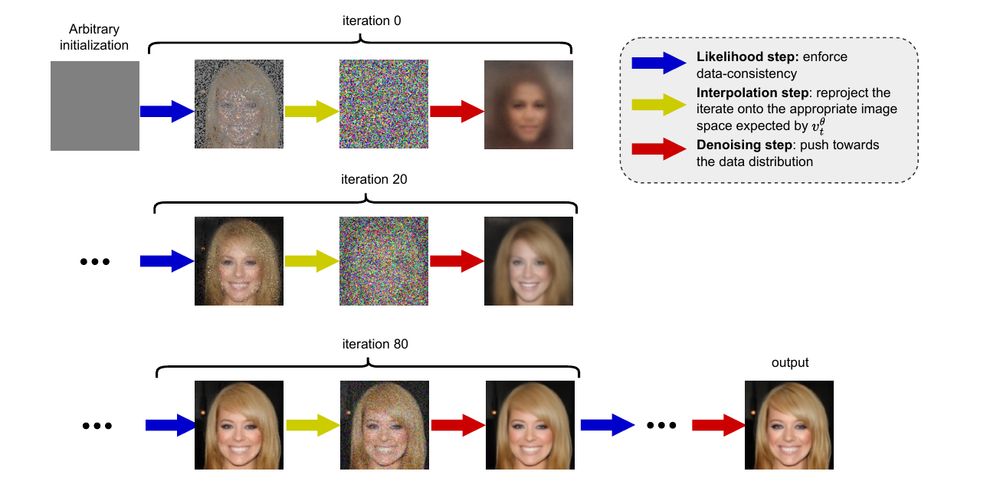
Our paper "PnP-Flow: Plug-and-Play Image Restoration with Flow Matching" has been accepted to ICLR 2025. Here a short explainer: We want to restore images (i.e., solve inverse problems) using pretrained velocity fields from flow matching. However, using change of variables is super costly.
January 23, 2025 at 10:53 AM
Our paper "PnP-Flow: Plug-and-Play Image Restoration with Flow Matching" has been accepted to ICLR 2025. Here a short explainer: We want to restore images (i.e., solve inverse problems) using pretrained velocity fields from flow matching. However, using change of variables is super costly.
In a somewhat recent paper we introduced conditional Wasserstein Distances. They generalize a property that basically explains why KL works well for generative modelling, the chain rule of KL!
It says that if one wants to approximate the posterior, one can also minimize the KL between joints.
It says that if one wants to approximate the posterior, one can also minimize the KL between joints.
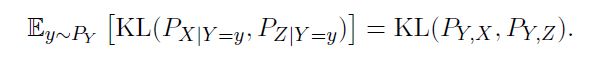
November 20, 2024 at 9:07 AM
In a somewhat recent paper we introduced conditional Wasserstein Distances. They generalize a property that basically explains why KL works well for generative modelling, the chain rule of KL!
It says that if one wants to approximate the posterior, one can also minimize the KL between joints.
It says that if one wants to approximate the posterior, one can also minimize the KL between joints.
Reposted by Paul Hagemann
I created a starter pack for simulation-based inference (aka. likelihood-free inference).
Let me know if you’d like me to add you.
go.bsky.app/GVnJRoK
Let me know if you’d like me to add you.
go.bsky.app/GVnJRoK
November 17, 2024 at 3:14 PM
I created a starter pack for simulation-based inference (aka. likelihood-free inference).
Let me know if you’d like me to add you.
go.bsky.app/GVnJRoK
Let me know if you’d like me to add you.
go.bsky.app/GVnJRoK

