computer graphics, programming systems, machine learning, differentiable graphics
The papers are:
groups.csail.mit.edu/graphics/xfo...
groups.csail.mit.edu/graphics/hdr...
likesum.github.io/bpn/
tamarott.github.io/ASAPNet_web/
The ones I didn't list here are good too. ; )



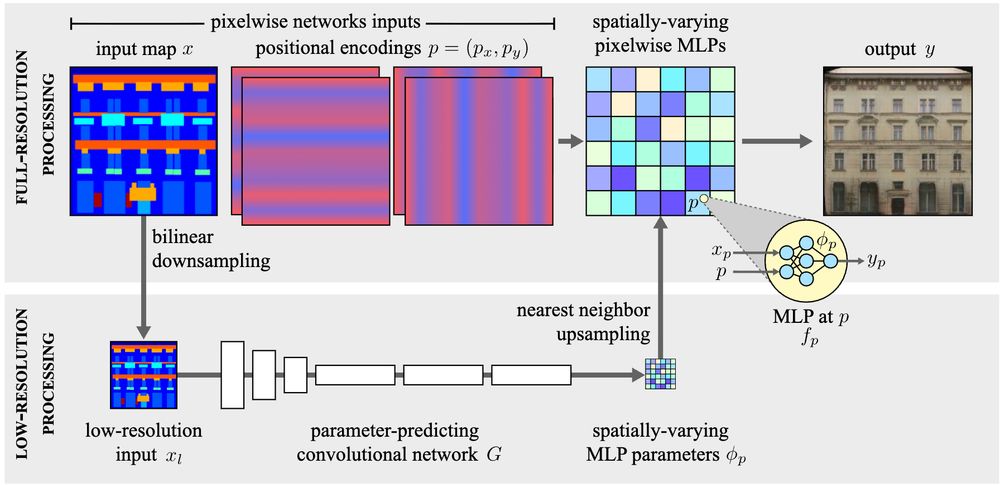
The papers are:
groups.csail.mit.edu/graphics/xfo...
groups.csail.mit.edu/graphics/hdr...
likesum.github.io/bpn/
tamarott.github.io/ASAPNet_web/
The ones I didn't list here are good too. ; )
Take a look if you are interested, or if you have an existential crisis of your graphics-related research or job!
Take a look if you are interested, or if you have an existential crisis of your graphics-related research or job!

Yes, I think it's official now : p

Yes, I think it's official now : p
In short, there is really no reason not to use RCV in your renderer and differentiable renderer. It reduces variance at negligible cost!
In short, there is really no reason not to use RCV in your renderer and differentiable renderer. It reduces variance at negligible cost!





