
2022 새해 오미쿠지는 2024 카레와 동일하게 5%였으므로 생략.
2023 새해 오미쿠지는 3%였으므로 아래와 같이 바뀔 것이다.
2022 새해 오미쿠지는 2024 카레와 동일하게 5%였으므로 생략.
2023 새해 오미쿠지는 3%였으므로 아래와 같이 바뀔 것이다.
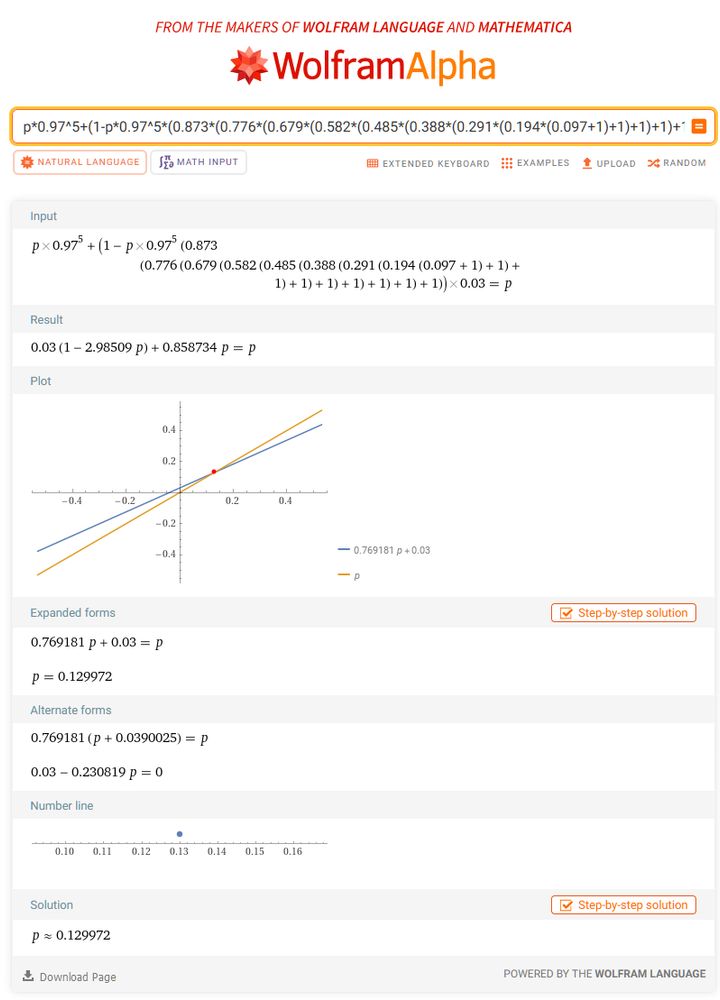
최종적으로, 15회 이후 시행에서 임의 번째 시행의 최고 등급 확률이 약 14.0365%라고 볼 수 있게 된 것이다!
어짜피 최종 효율 따질 땐 15회는 진작에 넘었을 테니 이걸 쓸 수 있게 된다.
계산하고 보니 첫 번째 상승한 확률인 14.5%에 살짝 못 미친다.
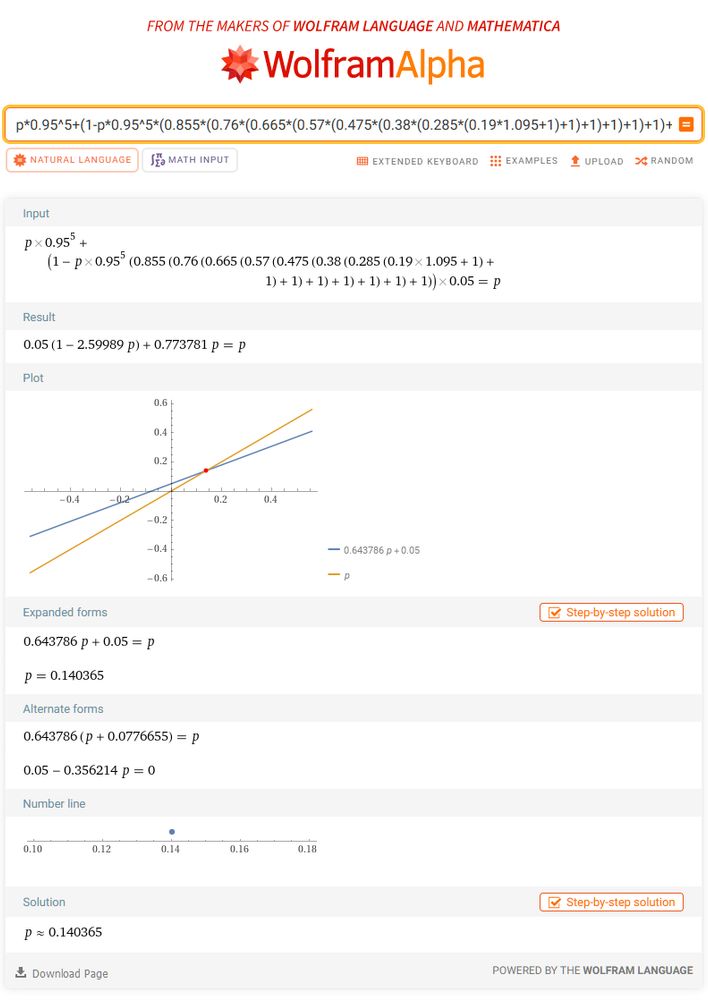
최종적으로, 15회 이후 시행에서 임의 번째 시행의 최고 등급 확률이 약 14.0365%라고 볼 수 있게 된 것이다!
어짜피 최종 효율 따질 땐 15회는 진작에 넘었을 테니 이걸 쓸 수 있게 된다.
계산하고 보니 첫 번째 상승한 확률인 14.5%에 살짝 못 미친다.
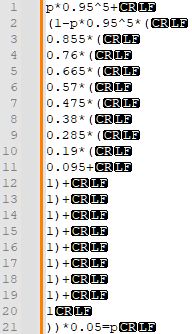
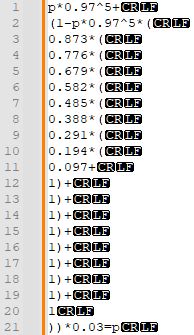
뭔가 또 묶을 게 보이는 것 같은데?
뭔가 또 묶을 게 보이는 것 같은데?

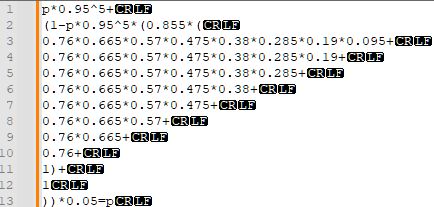
1~10번째 줄은 14~5연속만 안 나올 확률 각각에 다음 시행의 최고 등급 확률을 곱한 거고, 11번째 줄부터는 <5연속만 안 나올 확률을 구하고 0.05를 곱한 것이다. 끔찍하지만...
잘 보면 1~2번째 줄을 합하면 0.095*1+0.905=1이 되어 식을 줄일 수 있는 것이 보인다.

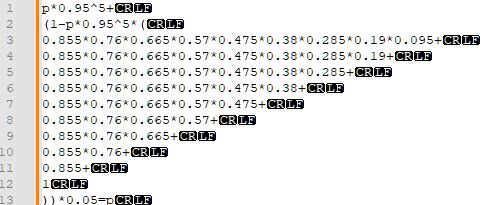
1~10번째 줄은 14~5연속만 안 나올 확률 각각에 다음 시행의 최고 등급 확률을 곱한 거고, 11번째 줄부터는 <5연속만 안 나올 확률을 구하고 0.05를 곱한 것이다. 끔찍하지만...
잘 보면 1~2번째 줄을 합하면 0.095*1+0.905=1이 되어 식을 줄일 수 있는 것이 보인다.
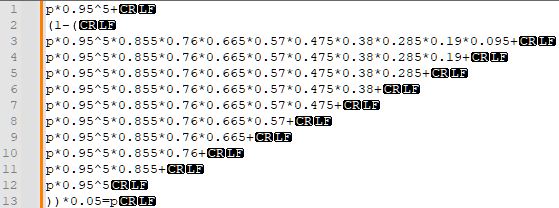
0.95^5*0.05, 아쉽지만 아닐 것이다. 왜냐고? 마지막으로 나온 최고 등급이 확률 보정을 안 받은 최고 등급일지 어떻게 아는가?
그럼 최종적으로 최고 등급이 나올 확률을 p라고 잡고, 0.95^5*p라고 해야 하겠지.
그러면 6회 연속만 안 나올 확률은? 0.95^6*p로 계산하면 안 된다. 확률 보정이 한 번 붙으니까, 0.95^5*0.855*p로 계산해야 한다. 이렇게 연속 5~14회만 안 나올 확률을 각각 구한다.
0.95^5*0.05, 아쉽지만 아닐 것이다. 왜냐고? 마지막으로 나온 최고 등급이 확률 보정을 안 받은 최고 등급일지 어떻게 아는가?
그럼 최종적으로 최고 등급이 나올 확률을 p라고 잡고, 0.95^5*p라고 해야 하겠지.
그러면 6회 연속만 안 나올 확률은? 0.95^6*p로 계산하면 안 된다. 확률 보정이 한 번 붙으니까, 0.95^5*0.855*p로 계산해야 한다. 이렇게 연속 5~14회만 안 나올 확률을 각각 구한다.
6회만큼이라면 5+9.5+9.5=24(%) 확률로 최고 등급이 나온다.
...이렇게, 직전 수행까지 정말 운 없게도 연속 14회만큼 안 나왔다면 5+95=100(%) 확률로 최고 등급이 나온다.
천장 시스템과 비슷하다고 말한 건 이것 때문.
그럼 확률 계산을 하려면, 먼저 연속 N회에 대한 조건부 확률을 구해야겠지? 직전 수행까지 연속 5회만큼 안 나온 시점부터. 4회까지는 확률에 변동이 없다.
6회만큼이라면 5+9.5+9.5=24(%) 확률로 최고 등급이 나온다.
...이렇게, 직전 수행까지 정말 운 없게도 연속 14회만큼 안 나왔다면 5+95=100(%) 확률로 최고 등급이 나온다.
천장 시스템과 비슷하다고 말한 건 이것 때문.
그럼 확률 계산을 하려면, 먼저 연속 N회에 대한 조건부 확률을 구해야겠지? 직전 수행까지 연속 5회만큼 안 나온 시점부터. 4회까지는 확률에 변동이 없다.

