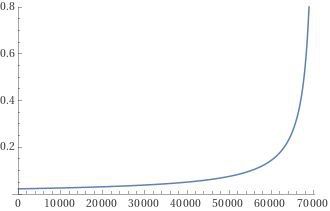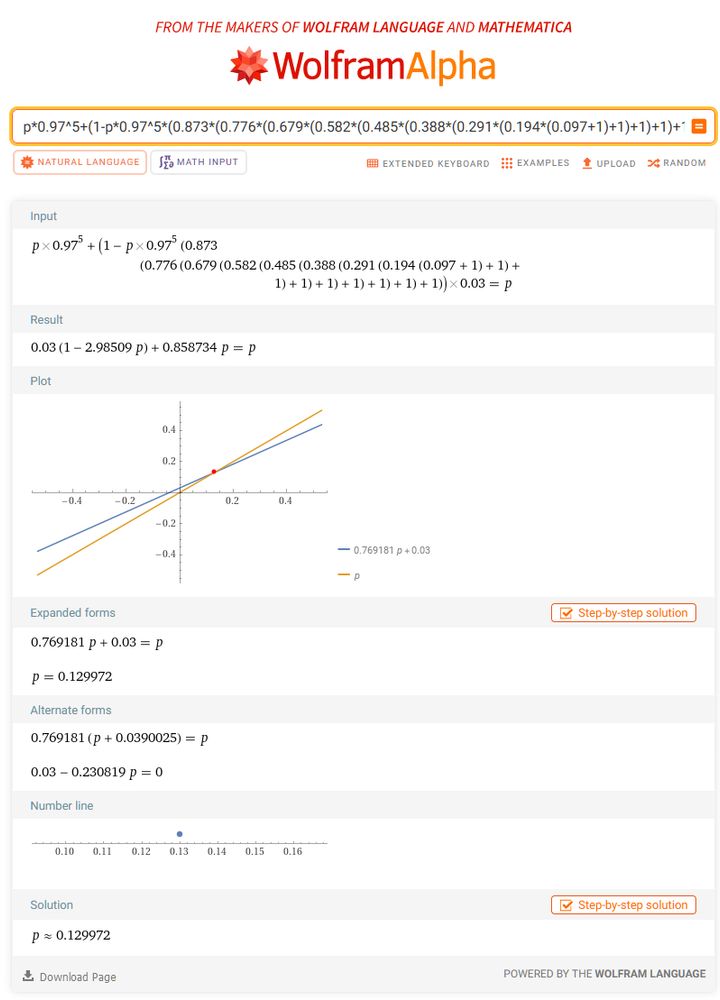
2022 새해 오미쿠지는 2024 카레와 동일하게 5%였으므로 생략.
2023 새해 오미쿠지는 3%였으므로 아래와 같이 바뀔 것이다.
2022 새해 오미쿠지는 2024 카레와 동일하게 5%였으므로 생략.
2023 새해 오미쿠지는 3%였으므로 아래와 같이 바뀔 것이다.
최종적으로, 15회 이후 시행에서 임의 번째 시행의 최고 등급 확률이 약 14.0365%라고 볼 수 있게 된 것이다!
어짜피 최종 효율 따질 땐 15회는 진작에 넘었을 테니 이걸 쓸 수 있게 된다.
계산하고 보니 첫 번째 상승한 확률인 14.5%에 살짝 못 미친다.
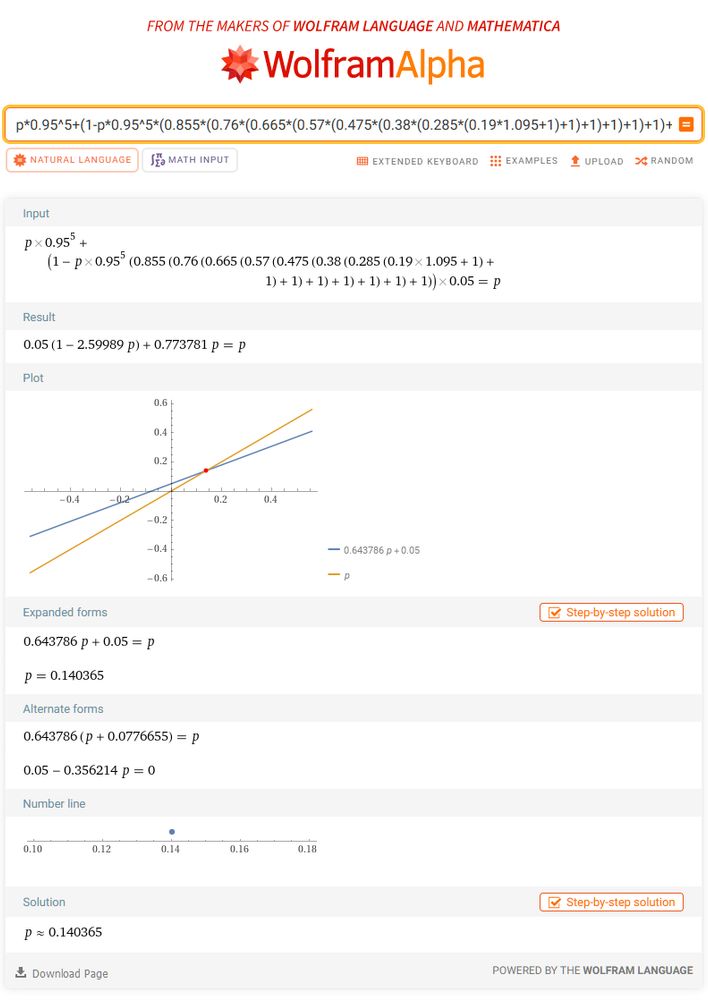
최종적으로, 15회 이후 시행에서 임의 번째 시행의 최고 등급 확률이 약 14.0365%라고 볼 수 있게 된 것이다!
어짜피 최종 효율 따질 땐 15회는 진작에 넘었을 테니 이걸 쓸 수 있게 된다.
계산하고 보니 첫 번째 상승한 확률인 14.5%에 살짝 못 미친다.
뭔가 또 묶을 게 보이는 것 같은데?
뭔가 또 묶을 게 보이는 것 같은데?
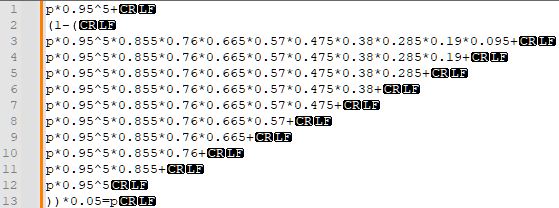

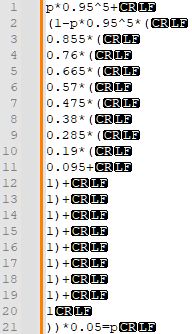
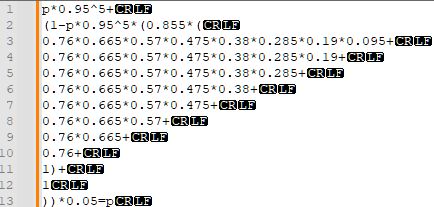
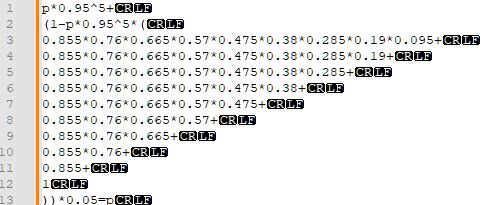
1~10번째 줄은 14~5연속만 안 나올 확률 각각에 다음 시행의 최고 등급 확률을 곱한 거고, 11번째 줄부터는 <5연속만 안 나올 확률을 구하고 0.05를 곱한 것이다. 끔찍하지만...
잘 보면 1~2번째 줄을 합하면 0.095*1+0.905=1이 되어 식을 줄일 수 있는 것이 보인다.

1~10번째 줄은 14~5연속만 안 나올 확률 각각에 다음 시행의 최고 등급 확률을 곱한 거고, 11번째 줄부터는 <5연속만 안 나올 확률을 구하고 0.05를 곱한 것이다. 끔찍하지만...
잘 보면 1~2번째 줄을 합하면 0.095*1+0.905=1이 되어 식을 줄일 수 있는 것이 보인다.
사실 이번 건 만든 건 아니고 재활용이긴 하지만...

사실 이번 건 만든 건 아니고 재활용이긴 하지만...