
一式陸攻の設計者٠本庄技師が、これまた一式陸攻の超々ジェラルミンを流用して作った伝説の自転車。乗ってみたいなぁ。

一式陸攻の設計者٠本庄技師が、これまた一式陸攻の超々ジェラルミンを流用して作った伝説の自転車。乗ってみたいなぁ。
鏡Iをまわして天体Sからの光を水平鏡Hに反射させ、その像を望遠鏡Tから見て、Sの高度a=∠SAHを測ります。
【六分儀の測角原理】
I,Hを通る各鏡の垂線の交点をB,
鏡の延長線の交点をCとすれば、
I,HはBCを直径とする円周上にある。
△IHAにおいてa+2β=2α
△IHBにおいてγ+β=α
∴a=2γ
Iを中心に動く指針の基準線IEを
HCと平行に作っておけば、
∠EIC=∠ICH=γ
よって、弧ED上にEを0°としてγの2倍になるように目盛りを刻んでおけば、Dの値を読むことでSの高度aが分かる。



鏡Iをまわして天体Sからの光を水平鏡Hに反射させ、その像を望遠鏡Tから見て、Sの高度a=∠SAHを測ります。
【六分儀の測角原理】
I,Hを通る各鏡の垂線の交点をB,
鏡の延長線の交点をCとすれば、
I,HはBCを直径とする円周上にある。
△IHAにおいてa+2β=2α
△IHBにおいてγ+β=α
∴a=2γ
Iを中心に動く指針の基準線IEを
HCと平行に作っておけば、
∠EIC=∠ICH=γ
よって、弧ED上にEを0°としてγの2倍になるように目盛りを刻んでおけば、Dの値を読むことでSの高度aが分かる。



寺内艦長による三角定規を使った対空戦闘術があまりにも有名。
SBDドーントレス急降下爆撃機は、
爆撃時に60°の角度でダイブしてくる。三角定規を敵機に合わせて覗き込めば、こちらが狙われているかどうか一発で分かるという。


寺内艦長による三角定規を使った対空戦闘術があまりにも有名。
SBDドーントレス急降下爆撃機は、
爆撃時に60°の角度でダイブしてくる。三角定規を敵機に合わせて覗き込めば、こちらが狙われているかどうか一発で分かるという。
Pickett N3-ESをそのまま半分に縮めたバリエーションで、32種の尺配置(√や³√を1種とカウントすれば29種)。縦幅がN3-ESと同サイズで、カーソル等のパーツが全て流用可というアメリカンな設計思想。その結果、ポケットに収まらぬデカ板が爆誕。
…もしN600同等のコンパクト設計で頑張ってくれたら、縦1.8㎝横4㎝は小さくなり、HEMMI №149A並みの携帯性能を獲得できた筈で、そうなればアポロに載って月に行った計算尺は、此方だったかも知れない。



Pickett N3-ESをそのまま半分に縮めたバリエーションで、32種の尺配置(√や³√を1種とカウントすれば29種)。縦幅がN3-ESと同サイズで、カーソル等のパーツが全て流用可というアメリカンな設計思想。その結果、ポケットに収まらぬデカ板が爆誕。
…もしN600同等のコンパクト設計で頑張ってくれたら、縦1.8㎝横4㎝は小さくなり、HEMMI №149A並みの携帯性能を獲得できた筈で、そうなればアポロに載って月に行った計算尺は、此方だったかも知れない。
①S尺35にカーソルを合わせて(sin35°)
②カーソルにC尺40を合わせて(÷40)
③C尺15にカーソル合わせると(×15)
カーソル下のS尺に
A=sin¯¹(sin35°÷40×15)≒12.42°が出る。
多分、今でもコレが最速じゃないだろうか。
①S尺35にカーソルを合わせて(sin35°)
②カーソルにC尺40を合わせて(÷40)
③C尺15にカーソル合わせると(×15)
カーソル下のS尺に
A=sin¯¹(sin35°÷40×15)≒12.42°が出る。
多分、今でもコレが最速じゃないだろうか。
おそらく専用の計算尺を使ったはず。(汎用でも十分)
計算尺が武器だという世間の認識は、強ち間違ってはいない。
٠雷速40㏏
٠目標船速15㏏
٠目標進路(方位角)35°
の場合で射角Aを求めると
sinA=(15/40)sin35°
sin¯¹A≒12.42°
でも戦闘機乗りだとコンマ何秒で未来位置計算しなきゃだから、計算尺なんて使ってられない。無意識下で小脳がフル回転。
おそらく専用の計算尺を使ったはず。(汎用でも十分)
計算尺が武器だという世間の認識は、強ち間違ってはいない。
٠雷速40㏏
٠目標船速15㏏
٠目標進路(方位角)35°
の場合で射角Aを求めると
sinA=(15/40)sin35°
sin¯¹A≒12.42°
でも戦闘機乗りだとコンマ何秒で未来位置計算しなきゃだから、計算尺なんて使ってられない。無意識下で小脳がフル回転。
攪乱要素を除くと、必要なのは彼我の速度と目標の進路。正弦定理を使って射角を求める。
意外にも、距離は関係無い。

攪乱要素を除くと、必要なのは彼我の速度と目標の進路。正弦定理を使って射角を求める。
意外にも、距離は関係無い。
それはそうと、この解法。計算尺の練習問題として、実にイイ感じなのであります!
計算の手数は少ないのに、A,B,C,D,S,T尺を満遍なく使い、計算尺の基本操作を一通り押さえています。
٠比例計算で係数を一発で揃える
٠平方根の入った計算と大小判定
٠三角関数と逆三角関数の使い方
٠逆数を使った手数の短縮
など、汎用性の高い小技が使われます。手順短絡による高速化って感じで、何となく古武術的な趣だなー。



それはそうと、この解法。計算尺の練習問題として、実にイイ感じなのであります!
計算の手数は少ないのに、A,B,C,D,S,T尺を満遍なく使い、計算尺の基本操作を一通り押さえています。
٠比例計算で係数を一発で揃える
٠平方根の入った計算と大小判定
٠三角関数と逆三角関数の使い方
٠逆数を使った手数の短縮
など、汎用性の高い小技が使われます。手順短絡による高速化って感じで、何となく古武術的な趣だなー。


…隣の家が2~3年ほど伸び放題に放置した山桑が、実をつけるまでになりました。ニセアカシアと同じくらい成長速いのな。

…隣の家が2~3年ほど伸び放題に放置した山桑が、実をつけるまでになりました。ニセアカシアと同じくらい成長速いのな。
二次方程式の斬新すぎる解法が載ってた。完全に計算尺の利用を前提にしていて、ちょっと普通の発想じゃ思い付けない。
x²±2pxーq=0
の形だと
√q÷p=tan2θ
としてθを求め、
x₁=±√q×tanθ
x₂=∓√q×cotθ
で解が求まる。
やってみるとわかるけど、計算尺だとかなり早い。しかも、解が一つ解った時点で解と係数の関係を使えば、更に一手省略できる。



二次方程式の斬新すぎる解法が載ってた。完全に計算尺の利用を前提にしていて、ちょっと普通の発想じゃ思い付けない。
x²±2pxーq=0
の形だと
√q÷p=tan2θ
としてθを求め、
x₁=±√q×tanθ
x₂=∓√q×cotθ
で解が求まる。
やってみるとわかるけど、計算尺だとかなり早い。しかも、解が一つ解った時点で解と係数の関係を使えば、更に一手省略できる。
三角関数尺(S,T,ST尺)とCI尺が同じ面に配置されてるので、裏返す手間が省けて地味に計算しやすく、お気に入りの計算尺。
動画の計算例は
sin20°+sin50°≒1.108
三手で計算できます。
①カーソルをsin20°に合わす
②カーソルにsin50°を合わすと
sin20°:sin50° ≒ 1:2.24が分かる
③CI尺に1+2.24=3.24をとってカーソルに合わせると
sin20°+sin50°
=sin20°×3.24≒1.108
三角関数尺(S,T,ST尺)とCI尺が同じ面に配置されてるので、裏返す手間が省けて地味に計算しやすく、お気に入りの計算尺。
動画の計算例は
sin20°+sin50°≒1.108
三手で計算できます。
①カーソルをsin20°に合わす
②カーソルにsin50°を合わすと
sin20°:sin50° ≒ 1:2.24が分かる
③CI尺に1+2.24=3.24をとってカーソルに合わせると
sin20°+sin50°
=sin20°×3.24≒1.108
5インチのポケット計算尺のハズなんだが、ちょっとデカ過ぎてポケットには入らんよな…
Pickett N600-ESと同じ5インチとか言われても全然そう見えんし、何なら6インチのHEMMI No.136よりデカいし、8インチ尺とほぼ同じサイズ感…



5インチのポケット計算尺のハズなんだが、ちょっとデカ過ぎてポケットには入らんよな…
Pickett N600-ESと同じ5インチとか言われても全然そう見えんし、何なら6インチのHEMMI No.136よりデカいし、8インチ尺とほぼ同じサイズ感…
あと、戦前の計算尺で固定尺に記載されてたprodー1、quot+1 の表記なんかも、円形計算尺で考えると意味が直感的にわかりやすい。


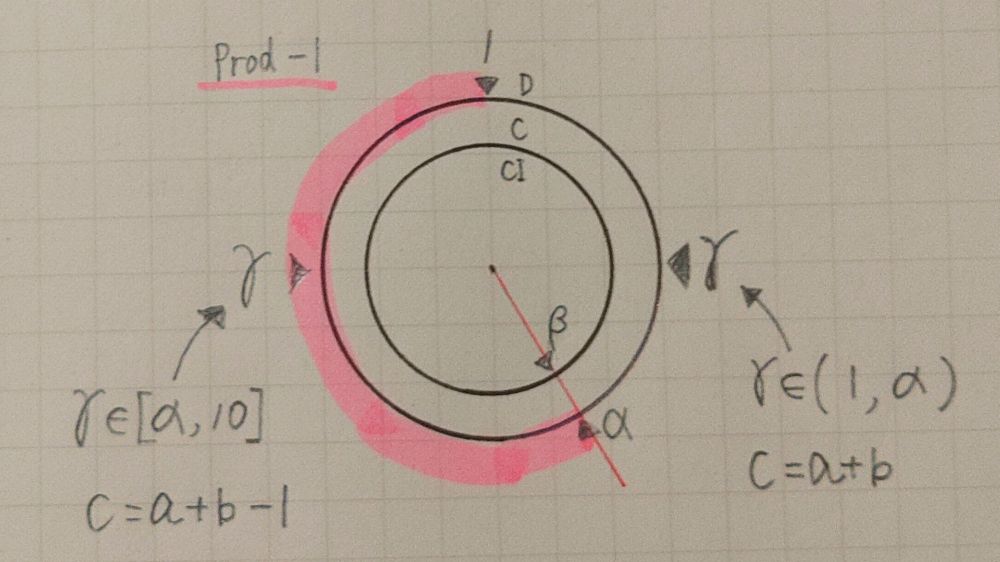
あと、戦前の計算尺で固定尺に記載されてたprodー1、quot+1 の表記なんかも、円形計算尺で考えると意味が直感的にわかりやすい。
A÷B=C のとき、
A,B,Cの有効数字を各々α,β,γ
指数部を各々a,b,cとする。
計算尺では以下の操作①②を行い、
Cの有効数字γを求める。
①D尺上にαをとり、
D尺を[1, α]と(α, 10)の
2つの区間に分割する。
②C尺βをD尺αに合わせて、
滑尺基線下のD尺にγを得る。
(又は、滑尺基線をD尺αに合わせて
CI尺β下のD尺にγを得る。)
この時、C=γ×10^cについて
γ∈[1, α] ⇔ c=aーb+1
γ∈(α, 10) ⇔ c=aーb
が成立する。


A÷B=C のとき、
A,B,Cの有効数字を各々α,β,γ
指数部を各々a,b,cとする。
計算尺では以下の操作①②を行い、
Cの有効数字γを求める。
①D尺上にαをとり、
D尺を[1, α]と(α, 10)の
2つの区間に分割する。
②C尺βをD尺αに合わせて、
滑尺基線下のD尺にγを得る。
(又は、滑尺基線をD尺αに合わせて
CI尺β下のD尺にγを得る。)
この時、C=γ×10^cについて
γ∈[1, α] ⇔ c=aーb+1
γ∈(α, 10) ⇔ c=aーb
が成立する。
A×B=C のとき、
A,B,Cの有効数字を各々α,β,γ
指数部を各々a,b,cとする。
計算尺では以下の操作①②を行い、
Cの有効数字γを求める。
①D尺上にαをとり、
D尺を(1, α)と[α, 10]の
2つの区間に分割する。
②CI尺のβをD尺のαに合わせて、
滑尺基線下のD尺にγを得る。
(又は、滑尺基線をD尺αに合わせて
C尺β下のD尺にγを得る。)
この時、C=γ×10^cについて
γ∈(1, α)⇔ c=a+b
γ∈[α, 10] ⇔ c=a+bー1
が成立する。


A×B=C のとき、
A,B,Cの有効数字を各々α,β,γ
指数部を各々a,b,cとする。
計算尺では以下の操作①②を行い、
Cの有効数字γを求める。
①D尺上にαをとり、
D尺を(1, α)と[α, 10]の
2つの区間に分割する。
②CI尺のβをD尺のαに合わせて、
滑尺基線下のD尺にγを得る。
(又は、滑尺基線をD尺αに合わせて
C尺β下のD尺にγを得る。)
この時、C=γ×10^cについて
γ∈(1, α)⇔ c=a+b
γ∈[α, 10] ⇔ c=a+bー1
が成立する。
12,345,678÷36,925,814
①有効数字の計算
D尺の1.235にカーソルを置いて
カーソルにC尺の3.69を合わせると
→右基線下のD尺に3.34を得る
②位取り計算 (割り算)
A,B,Cの位数を各々a,b,cとする。
A÷B=Cのとき、
D尺上のAとCの有効数字を比べ
C<Aなら c=aーb+1
A≦Cなら c=aーb
今回は①より1.235<3.34なので
位数はc=aーb=8ー8=0
∴ 12,345,678÷36,925,814
≒0.334
=3.34×10¯¹

12,345,678÷36,925,814
①有効数字の計算
D尺の1.235にカーソルを置いて
カーソルにC尺の3.69を合わせると
→右基線下のD尺に3.34を得る
②位取り計算 (割り算)
A,B,Cの位数を各々a,b,cとする。
A÷B=Cのとき、
D尺上のAとCの有効数字を比べ
C<Aなら c=aーb+1
A≦Cなら c=aーb
今回は①より1.235<3.34なので
位数はc=aーb=8ー8=0
∴ 12,345,678÷36,925,814
≒0.334
=3.34×10¯¹
12,345,678×36,925,814
①有効数字の計算
D尺の1.235にカーソルを置いて
カーソルにCI尺の3.69を合わせる
→右基線下のD尺に4.56を得る
②位取り計算(掛け算)
A,B,Cの位数を各々a,b,cとする。
A×B=Cのとき
D尺上のAとCの有効数字を比べ
C<Aなら c=a+b
A≦Cなら c=a+bー1 になる。
今回は①より1.235<4.56なので
c=a+bー1=8+8ー1=15
∴ 12,345,678×36,925,814
≒456,000,000,000,000
=4.56×10¹⁴


12,345,678×36,925,814
①有効数字の計算
D尺の1.235にカーソルを置いて
カーソルにCI尺の3.69を合わせる
→右基線下のD尺に4.56を得る
②位取り計算(掛け算)
A,B,Cの位数を各々a,b,cとする。
A×B=Cのとき
D尺上のAとCの有効数字を比べ
C<Aなら c=a+b
A≦Cなら c=a+bー1 になる。
今回は①より1.235<4.56なので
c=a+bー1=8+8ー1=15
∴ 12,345,678×36,925,814
≒456,000,000,000,000
=4.56×10¹⁴
ただ、実際上の操作性を考えるならば、やはり滑尺の位置を基準にした方が分かり易い。
慣れれば計算尺での仮数部計算と同時に指数部のカウントが行われるので、電卓よりも素早く計算することが出来るようになる。


ただ、実際上の操作性を考えるならば、やはり滑尺の位置を基準にした方が分かり易い。
慣れれば計算尺での仮数部計算と同時に指数部のカウントが行われるので、電卓よりも素早く計算することが出来るようになる。
この場合の位取りはとても簡単で、各数値の指数部を単純に合計(掛け算は+、割り算はー)し、各演算時の「滑尺位置が右側に出ている時」だけ、掛け算の場合はー1、割り算の場合は+1してやればいい。
戦前計算尺に見られる「Prodー1」や「Quot+1」の表記はおそらく上記の意味で記載されていると思われる。
もしそうだとすればCI尺が装備されると表記が逆になってしまうから、混乱を招く不要なモノとして廃止されていったという説も成り立ちそうだ。



この場合の位取りはとても簡単で、各数値の指数部を単純に合計(掛け算は+、割り算はー)し、各演算時の「滑尺位置が右側に出ている時」だけ、掛け算の場合はー1、割り算の場合は+1してやればいい。
戦前計算尺に見られる「Prodー1」や「Quot+1」の表記はおそらく上記の意味で記載されていると思われる。
もしそうだとすればCI尺が装備されると表記が逆になってしまうから、混乱を招く不要なモノとして廃止されていったという説も成り立ちそうだ。
こいつはたまりませんな。ぐへへ…
国鉄といえば、予定ダイヤから逆算して時速何㎞で走らせる必要があるって場合に、D51やC62など機関車毎に異なる牽引力と路線毎の勾配と速度を考慮して、この区間で牽ける客車は最大何両編成とか、そういう計算を緻密にやってるイメージがありまして。
暗算や算盤だと流石に厳しいこの手の計算を、電卓も無いあの時代に平然とこなしていた国鉄マンはホント凄いって尊敬していました。計算尺の達人がゴロゴロしてたんでしょうね。



こいつはたまりませんな。ぐへへ…
国鉄といえば、予定ダイヤから逆算して時速何㎞で走らせる必要があるって場合に、D51やC62など機関車毎に異なる牽引力と路線毎の勾配と速度を考慮して、この区間で牽ける客車は最大何両編成とか、そういう計算を緻密にやってるイメージがありまして。
暗算や算盤だと流石に厳しいこの手の計算を、電卓も無いあの時代に平然とこなしていた国鉄マンはホント凄いって尊敬していました。計算尺の達人がゴロゴロしてたんでしょうね。
Pickett N904-ES
位取り用計算尺です。
表面の尺は
固定尺:K,A,D,L
滑尺:B,T,S,CI,C
でオーソドックスな配置。
しかし裏面が独特。
縮尺を1/20にして、表と同じ尺配置にしてあります。
これにより、位取りが視覚的に把握できる仕組みになっています。
表で有効数字を、裏で小数点位置を把握して、答えを出そうというアイデアです。




Pickett N904-ES
位取り用計算尺です。
表面の尺は
固定尺:K,A,D,L
滑尺:B,T,S,CI,C
でオーソドックスな配置。
しかし裏面が独特。
縮尺を1/20にして、表と同じ尺配置にしてあります。
これにより、位取りが視覚的に把握できる仕組みになっています。
表で有効数字を、裏で小数点位置を把握して、答えを出そうというアイデアです。


