
www.rohitlamba.com







1/2* 4 + 1/2* 2 > 1/2* 5 + 1/2* 0.
So, (G,G) is the SSE.
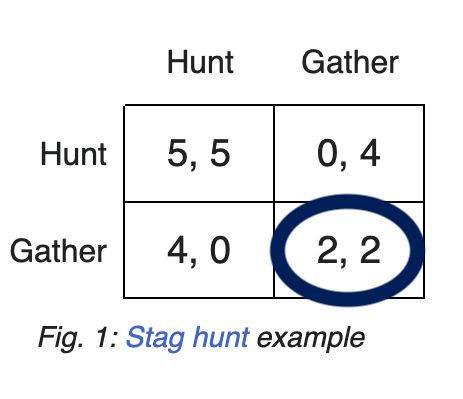
1/2* 4 + 1/2* 2 > 1/2* 5 + 1/2* 0.
So, (G,G) is the SSE.






[Though implementing inheritance taxes well has been hard.]

[Though implementing inheritance taxes well has been hard.]

