
arxiv.org/abs/2509.11801

arxiv.org/abs/2509.11801












iopscience.iop.org/article/10.1...

iopscience.iop.org/article/10.1...





arxiv.org/pdf/2505.05246
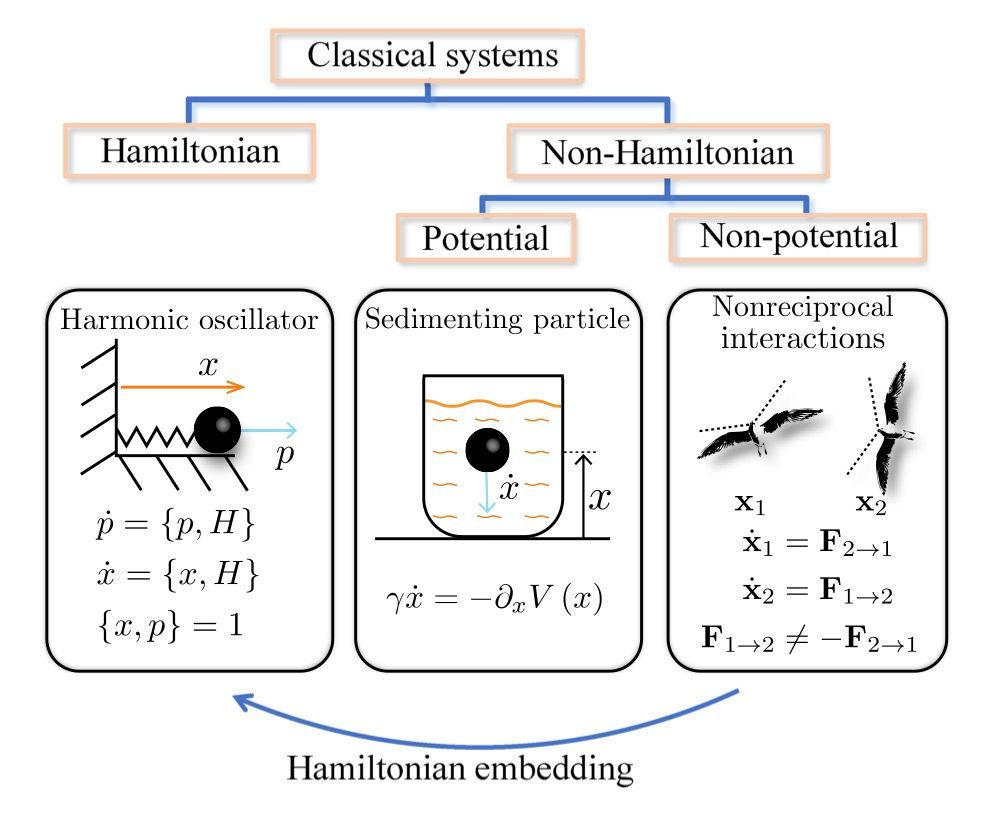
arxiv.org/pdf/2505.05246



