Head of interpretability research at EleutherAI, but posts are my own views, not Eleuther’s.

And networks which memorize their training data without generalizing have lower local volume— higher complexity— than generalizing ones.

And networks which memorize their training data without generalizing have lower local volume— higher complexity— than generalizing ones.
Importance sampling using gradient info helps address this issue by making us more likely to sample outliers.

Importance sampling using gradient info helps address this issue by making us more likely to sample outliers.
The distance from the anchor to the edge of the region, along the random direction, gives us an estimate of how big (or how probable) the region is as a whole.

The distance from the anchor to the edge of the region, along the random direction, gives us an estimate of how big (or how probable) the region is as a whole.
We crunched the numbers and here's the answer:

We crunched the numbers and here's the answer:
you know you're on a roll when arxiv throttles you

you know you're on a roll when arxiv throttles you
We focused on a tiny 5K parameter MLP for most experiments, but we did find a similar SV spectrum in a 62K param image classifier.

We focused on a tiny 5K parameter MLP for most experiments, but we did find a similar SV spectrum in a 62K param image classifier.
This makes sense: training has to more aggressively compress parameter space in order to memorize unstructured data.

This makes sense: training has to more aggressively compress parameter space in order to memorize unstructured data.
Empirically though, we find a lot of overlap between bulks generated by different random inits. It appears to depend on the data, but only weakly on the labels.

Empirically though, we find a lot of overlap between bulks generated by different random inits. It appears to depend on the data, but only weakly on the labels.
There is also a chaotic subspace, with SVs greater than one, along which perturbations are magnified.
Training tends not to change parameters much along the bulk.

There is also a chaotic subspace, with SVs greater than one, along which perturbations are magnified.
Training tends not to change parameters much along the bulk.
Training will stretch, shrink, and rotate the sphere into an ellipsoid.
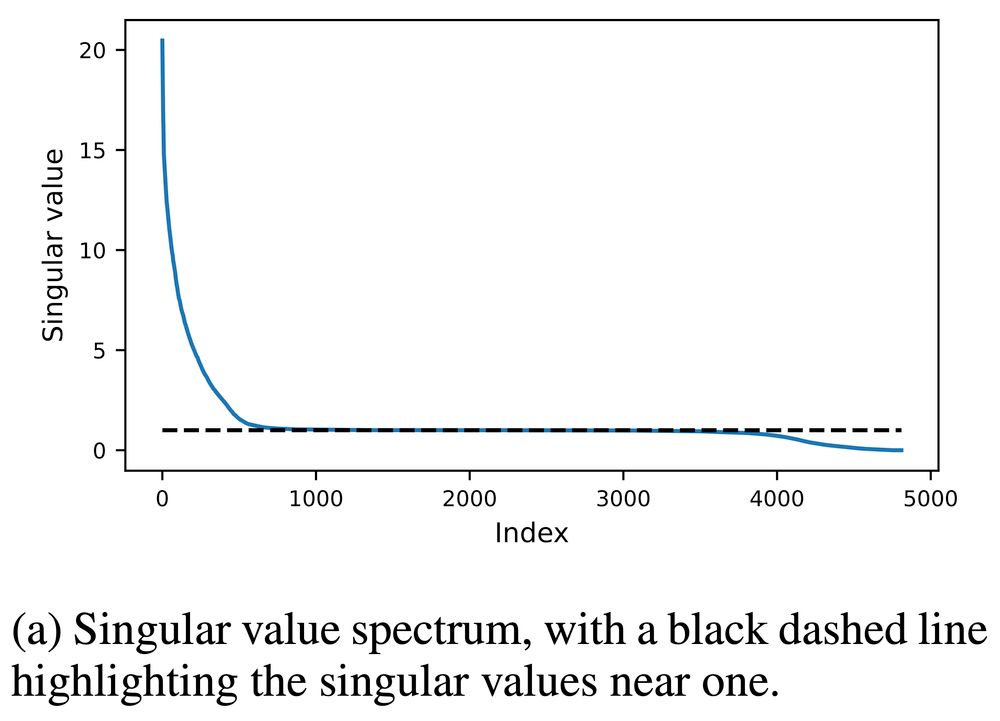
Jacobian singular values tell us the radii of the principal axes of that ellipse. Here's what they look like. A lot of radii are close to one!

Training will stretch, shrink, and rotate the sphere into an ellipsoid.
Jacobian singular values tell us the radii of the principal axes of that ellipse. Here's what they look like. A lot of radii are close to one!
In this new paper, we answer this question by analyzing the training Jacobian, the matrix of derivatives of the final parameters with respect to the initial parameters.
https://arxiv.org/abs/2412.07003
In this new paper, we answer this question by analyzing the training Jacobian, the matrix of derivatives of the final parameters with respect to the initial parameters.
https://arxiv.org/abs/2412.07003

