nathanaelbosch.github.io
javascript:(function(){var url=window.location.href;if(url.match(/arxiv\.org\/pdf\//)){window.location.href=url.replace('/pdf/','/abs/');}else if(url.match(/openreview\.net\/pdf\?id=/)){window.location.href=url.replace('/pdf?id=','/forum?id=');}})();
```
javascript:(function(){var url=window.location.href;if(url.match(/arxiv\.org\/pdf\//)){window.location.href=url.replace('/pdf/','/abs/');}else if(url.match(/openreview\.net\/pdf\?id=/)){window.location.href=url.replace('/pdf?id=','/forum?id=');}})();
```
💻 github.com/nathanaelbos...
📖 nathanaelbosch.github.io/ProbNumDiffE...
▶️ www.youtube.com/watch?v=iH_G...
6/6
💻 github.com/nathanaelbos...
📖 nathanaelbosch.github.io/ProbNumDiffE...
▶️ www.youtube.com/watch?v=iH_G...
6/6
📄 Full thesis: tobias-lib.uni-tuebingen.de/xmlui/handle...
5/6
📄 Full thesis: tobias-lib.uni-tuebingen.de/xmlui/handle...
5/6
[2] tinyurl.com/2av3e4te
[3] tinyurl.com/bddfkwcu
4/6
[2] tinyurl.com/2av3e4te
[3] tinyurl.com/bddfkwcu
4/6
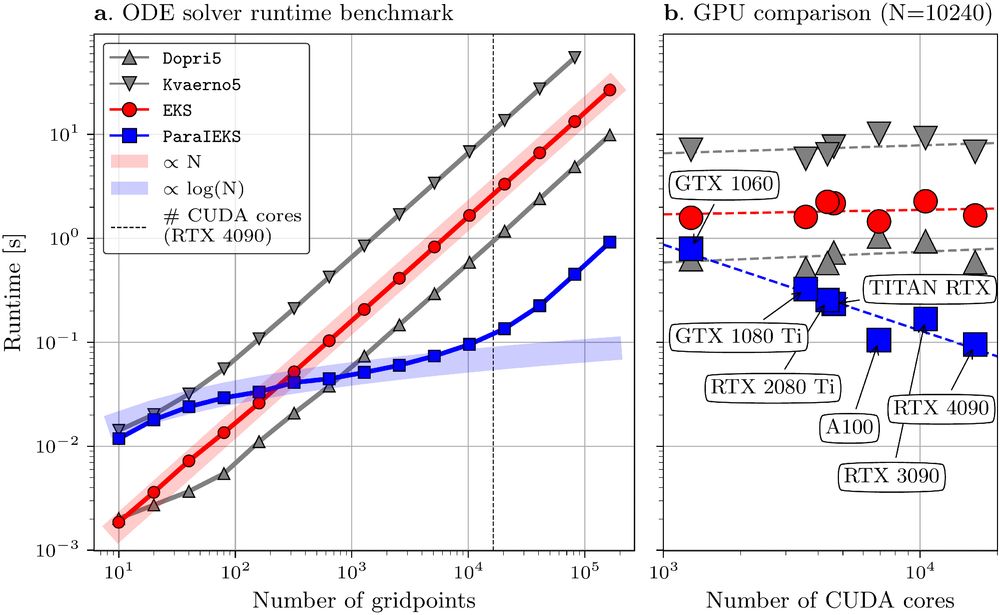
[1] www.jmlr.org/papers/v25/2...
3/6
[1] www.jmlr.org/papers/v25/2...
3/6
2/6
2/6

