nathanaelbosch.github.io
[2] tinyurl.com/2av3e4te
[3] tinyurl.com/bddfkwcu
4/6
[2] tinyurl.com/2av3e4te
[3] tinyurl.com/bddfkwcu
4/6
[1] www.jmlr.org/papers/v25/2...
3/6
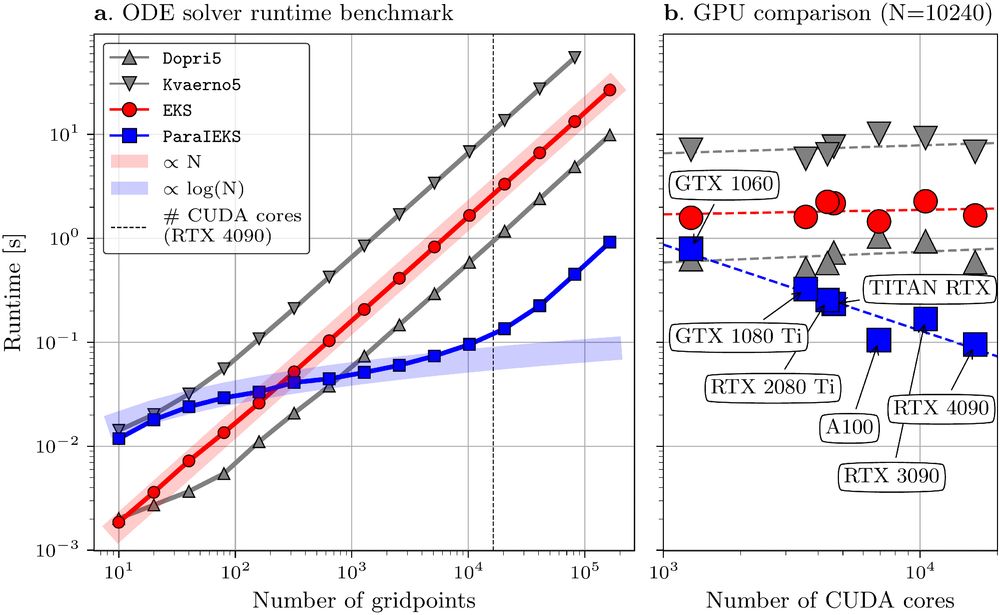
[1] www.jmlr.org/papers/v25/2...
3/6
2/6
2/6
📄 tinyurl.com/mt3sffb
🧵 1/6
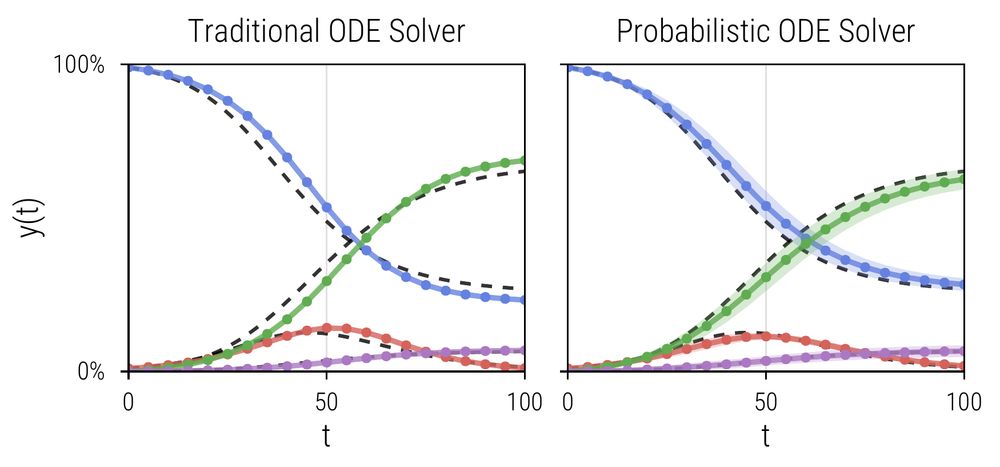
📄 tinyurl.com/mt3sffb
🧵 1/6

