Mathieu Dagréou
@matdag.bsky.social
Reposted by Mathieu Dagréou
AISTATS 2026 will be in Morocco!
July 30, 2025 at 8:07 AM
AISTATS 2026 will be in Morocco!
Reposted by Mathieu Dagréou
Tired of lengthy computations to derive scaling laws? This post is made for you: discover the sharpness of the z-transform!
francisbach.com/z-transform/
francisbach.com/z-transform/
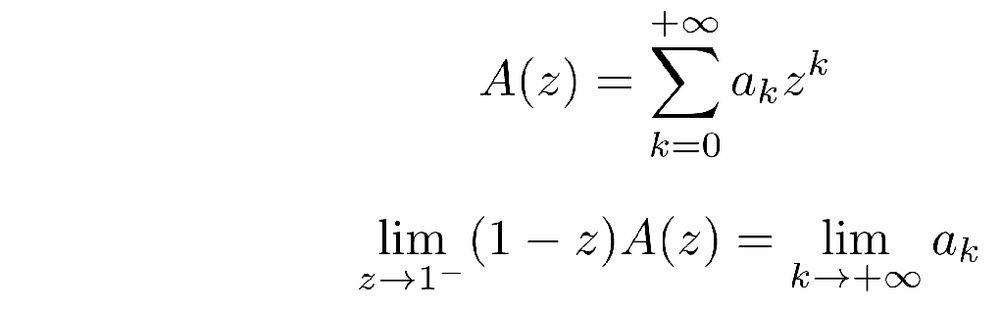
July 18, 2025 at 2:24 PM
Tired of lengthy computations to derive scaling laws? This post is made for you: discover the sharpness of the z-transform!
francisbach.com/z-transform/
francisbach.com/z-transform/
Reposted by Mathieu Dagréou
❓ How long does SGD take to reach the global minimum on non-convex functions?
With W. Azizian, J. Malick, P. Mertikopoulos, we tackle this fundamental question in our new ICML 2025 paper: "The Global Convergence Time of Stochastic Gradient Descent in Non-Convex Landscapes"
With W. Azizian, J. Malick, P. Mertikopoulos, we tackle this fundamental question in our new ICML 2025 paper: "The Global Convergence Time of Stochastic Gradient Descent in Non-Convex Landscapes"
June 18, 2025 at 1:59 PM
❓ How long does SGD take to reach the global minimum on non-convex functions?
With W. Azizian, J. Malick, P. Mertikopoulos, we tackle this fundamental question in our new ICML 2025 paper: "The Global Convergence Time of Stochastic Gradient Descent in Non-Convex Landscapes"
With W. Azizian, J. Malick, P. Mertikopoulos, we tackle this fundamental question in our new ICML 2025 paper: "The Global Convergence Time of Stochastic Gradient Descent in Non-Convex Landscapes"
Reposted by Mathieu Dagréou
New paper on the generalization of Flow Matching www.arxiv.org/abs/2506.03719
🤯 Why does flow matching generalize? Did you know that the flow matching target you're trying to learn *can only generate training points*?
w @quentinbertrand.bsky.social @annegnx.bsky.social @remiemonet.bsky.social 👇👇👇
🤯 Why does flow matching generalize? Did you know that the flow matching target you're trying to learn *can only generate training points*?
w @quentinbertrand.bsky.social @annegnx.bsky.social @remiemonet.bsky.social 👇👇👇
June 18, 2025 at 8:08 AM
New paper on the generalization of Flow Matching www.arxiv.org/abs/2506.03719
🤯 Why does flow matching generalize? Did you know that the flow matching target you're trying to learn *can only generate training points*?
w @quentinbertrand.bsky.social @annegnx.bsky.social @remiemonet.bsky.social 👇👇👇
🤯 Why does flow matching generalize? Did you know that the flow matching target you're trying to learn *can only generate training points*?
w @quentinbertrand.bsky.social @annegnx.bsky.social @remiemonet.bsky.social 👇👇👇
Reposted by Mathieu Dagréou
Register at PAISS 1-5 Sept 2025 @inria_grenoble with very talented speakers this year 🙂
paiss.inria.fr
cc @mvladimirova.bsky.social
paiss.inria.fr
cc @mvladimirova.bsky.social

June 9, 2025 at 8:55 PM
Register at PAISS 1-5 Sept 2025 @inria_grenoble with very talented speakers this year 🙂
paiss.inria.fr
cc @mvladimirova.bsky.social
paiss.inria.fr
cc @mvladimirova.bsky.social
Reposted by Mathieu Dagréou
🎉🎉🎉Our paper "Inexact subgradient methods for semialgebraic
functions" is accepted at Mathematical Programming !! This is a joint work with Jerome Bolte, Eric Moulines and Edouard Pauwels where we study a subgradient method with errors for nonconvex nonsmooth functions.
arxiv.org/pdf/2404.19517
functions" is accepted at Mathematical Programming !! This is a joint work with Jerome Bolte, Eric Moulines and Edouard Pauwels where we study a subgradient method with errors for nonconvex nonsmooth functions.
arxiv.org/pdf/2404.19517
arxiv.org
June 5, 2025 at 6:13 AM
🎉🎉🎉Our paper "Inexact subgradient methods for semialgebraic
functions" is accepted at Mathematical Programming !! This is a joint work with Jerome Bolte, Eric Moulines and Edouard Pauwels where we study a subgradient method with errors for nonconvex nonsmooth functions.
arxiv.org/pdf/2404.19517
functions" is accepted at Mathematical Programming !! This is a joint work with Jerome Bolte, Eric Moulines and Edouard Pauwels where we study a subgradient method with errors for nonconvex nonsmooth functions.
arxiv.org/pdf/2404.19517
Reposted by Mathieu Dagréou
I have cleaned a bit my lecture notes on Optimal Transport for Machine Learners arxiv.org/abs/2505.06589

Optimal Transport for Machine Learners
Optimal Transport is a foundational mathematical theory that connects optimization, partial differential equations, and probability. It offers a powerful framework for comparing probability distributi...
arxiv.org
May 13, 2025 at 5:18 AM
I have cleaned a bit my lecture notes on Optimal Transport for Machine Learners arxiv.org/abs/2505.06589
Reposted by Mathieu Dagréou
📣 New preprint 📣
**Differentiable Generalized Sliced Wasserstein Plans**
w/
L. Chapel
@rtavenar.bsky.social
We propose a Generalized Sliced Wasserstein method that provides an approximated transport plan and which admits a differentiable approximation.
arxiv.org/abs/2505.22049 1/5
**Differentiable Generalized Sliced Wasserstein Plans**
w/
L. Chapel
@rtavenar.bsky.social
We propose a Generalized Sliced Wasserstein method that provides an approximated transport plan and which admits a differentiable approximation.
arxiv.org/abs/2505.22049 1/5

June 2, 2025 at 2:40 PM
📣 New preprint 📣
**Differentiable Generalized Sliced Wasserstein Plans**
w/
L. Chapel
@rtavenar.bsky.social
We propose a Generalized Sliced Wasserstein method that provides an approximated transport plan and which admits a differentiable approximation.
arxiv.org/abs/2505.22049 1/5
**Differentiable Generalized Sliced Wasserstein Plans**
w/
L. Chapel
@rtavenar.bsky.social
We propose a Generalized Sliced Wasserstein method that provides an approximated transport plan and which admits a differentiable approximation.
arxiv.org/abs/2505.22049 1/5
Reposted by Mathieu Dagréou
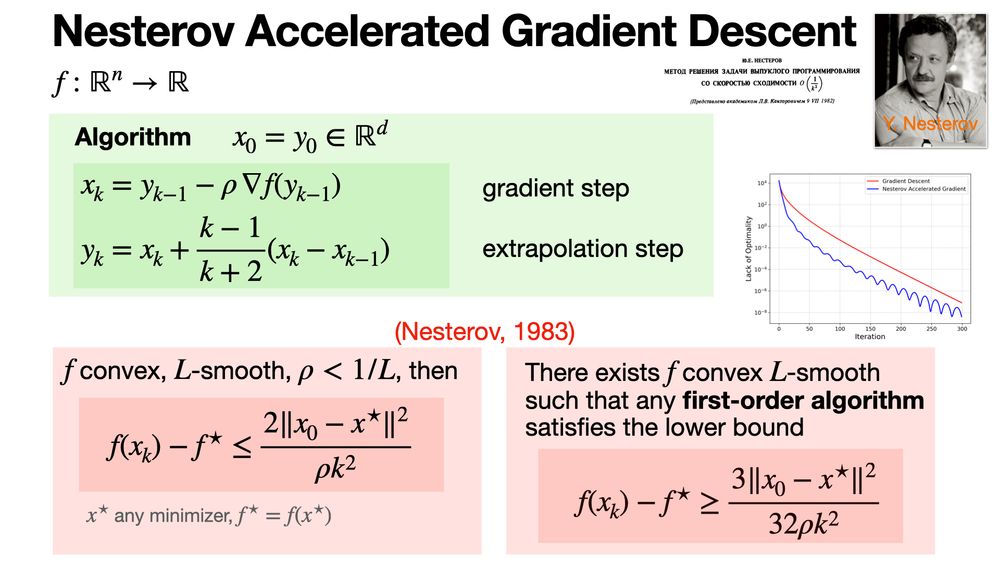
The Nesterov Accelerated Gradient (NAG) algorithm refines gradient descent by using an extrapolation step before computing the gradient. It leads to faster convergence for smooth convex functions, achieving the optimal rate of O(1/k^2). www.mathnet.ru/links/ceedfb...
April 25, 2025 at 5:01 AM
The Nesterov Accelerated Gradient (NAG) algorithm refines gradient descent by using an extrapolation step before computing the gradient. It leads to faster convergence for smooth convex functions, achieving the optimal rate of O(1/k^2). www.mathnet.ru/links/ceedfb...
Reposted by Mathieu Dagréou
Our paper
**Geometric and computational hardness of bilevel programming**
w/ Jerôme Bolte, Tùng Lê & Edouard Pauwels
has been accepted to Mathematical Programming!
We study how difficult it may be to solve bilevel optimization beyond strongly convex inner problems
arxiv.org/abs/2407.12372
**Geometric and computational hardness of bilevel programming**
w/ Jerôme Bolte, Tùng Lê & Edouard Pauwels
has been accepted to Mathematical Programming!
We study how difficult it may be to solve bilevel optimization beyond strongly convex inner problems
arxiv.org/abs/2407.12372

Geometric and computational hardness of bilevel programming
We first show a simple but striking result in bilevel optimization: unconstrained $C^\infty$ smooth bilevel programming is as hard as general extended-real-valued lower semicontinuous minimization. We...
arxiv.org
April 1, 2025 at 3:55 PM
Our paper
**Geometric and computational hardness of bilevel programming**
w/ Jerôme Bolte, Tùng Lê & Edouard Pauwels
has been accepted to Mathematical Programming!
We study how difficult it may be to solve bilevel optimization beyond strongly convex inner problems
arxiv.org/abs/2407.12372
**Geometric and computational hardness of bilevel programming**
w/ Jerôme Bolte, Tùng Lê & Edouard Pauwels
has been accepted to Mathematical Programming!
We study how difficult it may be to solve bilevel optimization beyond strongly convex inner problems
arxiv.org/abs/2407.12372
Reposted by Mathieu Dagréou
📣 New preprint 📣
Learning Theory for Kernel Bilevel Optimization
w/ @fareselkhoury.bsky.social E. Pauwels @michael-arbel.bsky.social
We provide generalization error bounds for bilevel optimization problems where the inner objective is minimized over a RKHS.
arxiv.org/abs/2502.08457
Learning Theory for Kernel Bilevel Optimization
w/ @fareselkhoury.bsky.social E. Pauwels @michael-arbel.bsky.social
We provide generalization error bounds for bilevel optimization problems where the inner objective is minimized over a RKHS.
arxiv.org/abs/2502.08457

February 20, 2025 at 1:55 PM
📣 New preprint 📣
Learning Theory for Kernel Bilevel Optimization
w/ @fareselkhoury.bsky.social E. Pauwels @michael-arbel.bsky.social
We provide generalization error bounds for bilevel optimization problems where the inner objective is minimized over a RKHS.
arxiv.org/abs/2502.08457
Learning Theory for Kernel Bilevel Optimization
w/ @fareselkhoury.bsky.social E. Pauwels @michael-arbel.bsky.social
We provide generalization error bounds for bilevel optimization problems where the inner objective is minimized over a RKHS.
arxiv.org/abs/2502.08457
Reposted by Mathieu Dagréou
Complex step approximation is a numerical method to approximate the derivative from a single function evaluation using complex arithmetic. It is some kind of “poor man” automatic differentiation. https://nhigham.com/2020/10/06/what-is-the-complex-step-approximation/

February 17, 2025 at 6:00 AM
Complex step approximation is a numerical method to approximate the derivative from a single function evaluation using complex arithmetic. It is some kind of “poor man” automatic differentiation. https://nhigham.com/2020/10/06/what-is-the-complex-step-approximation/
Reposted by Mathieu Dagréou
📢 New preprint 📢
Bilevel gradient methods and Morse parametric qualification
w/ J. Bolte, T. Lê, E. Pauwels
We study bilevel optimization with a nonconvex inner objective. To do so, we propose a new setting (Morse parametric qualification) to study bilevel algorithms.
arxiv.org/abs/2502.09074
Bilevel gradient methods and Morse parametric qualification
w/ J. Bolte, T. Lê, E. Pauwels
We study bilevel optimization with a nonconvex inner objective. To do so, we propose a new setting (Morse parametric qualification) to study bilevel algorithms.
arxiv.org/abs/2502.09074

February 14, 2025 at 10:18 AM
📢 New preprint 📢
Bilevel gradient methods and Morse parametric qualification
w/ J. Bolte, T. Lê, E. Pauwels
We study bilevel optimization with a nonconvex inner objective. To do so, we propose a new setting (Morse parametric qualification) to study bilevel algorithms.
arxiv.org/abs/2502.09074
Bilevel gradient methods and Morse parametric qualification
w/ J. Bolte, T. Lê, E. Pauwels
We study bilevel optimization with a nonconvex inner objective. To do so, we propose a new setting (Morse parametric qualification) to study bilevel algorithms.
arxiv.org/abs/2502.09074
Reposted by Mathieu Dagréou
My rant of the day: You can be rejected from an MSCA postdoctoral fellowship despite scoring almost the maximum in every category and receiving virtually no negative feedback. Before I explain why this is disastrous (assuming it is a common issue), a few comments.
February 10, 2025 at 7:28 AM
My rant of the day: You can be rejected from an MSCA postdoctoral fellowship despite scoring almost the maximum in every category and receiving virtually no negative feedback. Before I explain why this is disastrous (assuming it is a common issue), a few comments.
Reposted by Mathieu Dagréou
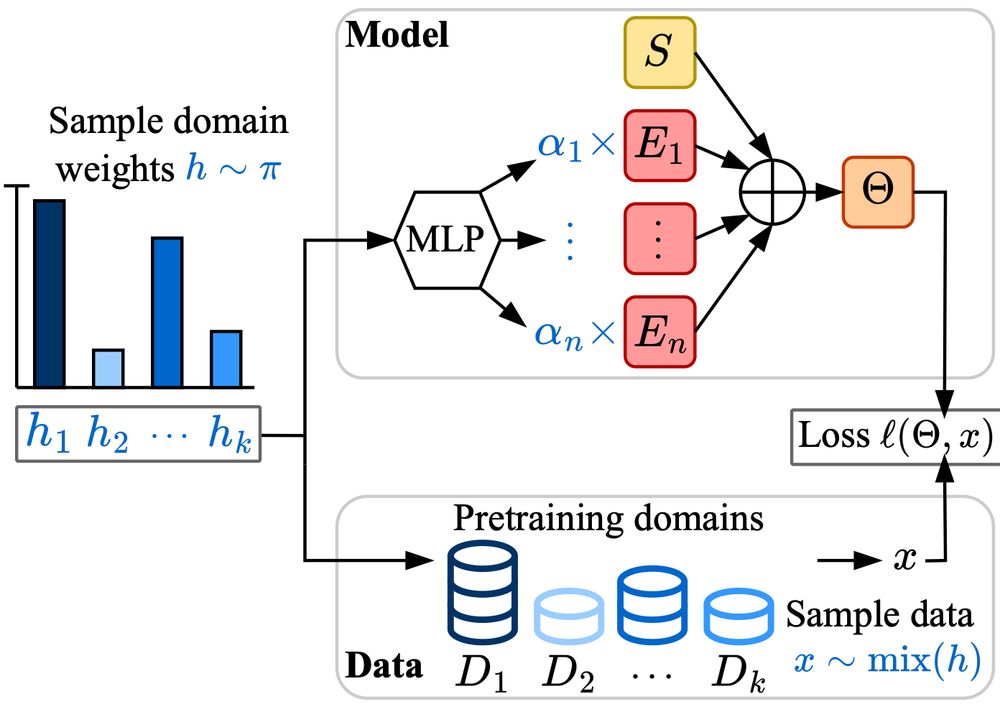
Excited to share Soup-of-Experts, a new neural network architecture that, for any given specific task, can instantiate in a flash a small model that is very good on it.
Made with ❤️ at Apple
Thanks to my co-authors David Grangier, Angelos Katharopoulos, and Skyler Seto!
arxiv.org/abs/2502.01804
Made with ❤️ at Apple
Thanks to my co-authors David Grangier, Angelos Katharopoulos, and Skyler Seto!
arxiv.org/abs/2502.01804
February 5, 2025 at 9:32 AM
Excited to share Soup-of-Experts, a new neural network architecture that, for any given specific task, can instantiate in a flash a small model that is very good on it.
Made with ❤️ at Apple
Thanks to my co-authors David Grangier, Angelos Katharopoulos, and Skyler Seto!
arxiv.org/abs/2502.01804
Made with ❤️ at Apple
Thanks to my co-authors David Grangier, Angelos Katharopoulos, and Skyler Seto!
arxiv.org/abs/2502.01804
Reposted by Mathieu Dagréou
Learning rate schedules seem mysterious? Why is the loss going down so fast during cooldown?
Turns out that this behaviour can be described with a bound from *convex, nonsmooth* optimization.
A short thread on our latest paper 🚞
arxiv.org/abs/2501.18965
Turns out that this behaviour can be described with a bound from *convex, nonsmooth* optimization.
A short thread on our latest paper 🚞
arxiv.org/abs/2501.18965

The Surprising Agreement Between Convex Optimization Theory and Learning-Rate Scheduling for Large Model Training
We show that learning-rate schedules for large model training behave surprisingly similar to a performance bound from non-smooth convex optimization theory. We provide a bound for the constant schedul...
arxiv.org
February 5, 2025 at 10:13 AM
Learning rate schedules seem mysterious? Why is the loss going down so fast during cooldown?
Turns out that this behaviour can be described with a bound from *convex, nonsmooth* optimization.
A short thread on our latest paper 🚞
arxiv.org/abs/2501.18965
Turns out that this behaviour can be described with a bound from *convex, nonsmooth* optimization.
A short thread on our latest paper 🚞
arxiv.org/abs/2501.18965
Reposted by Mathieu Dagréou
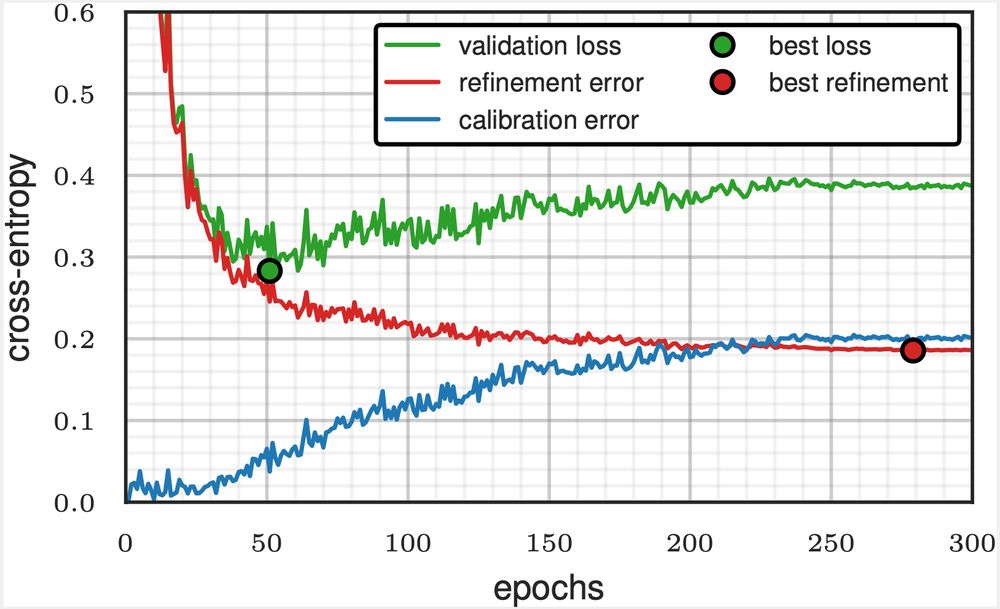
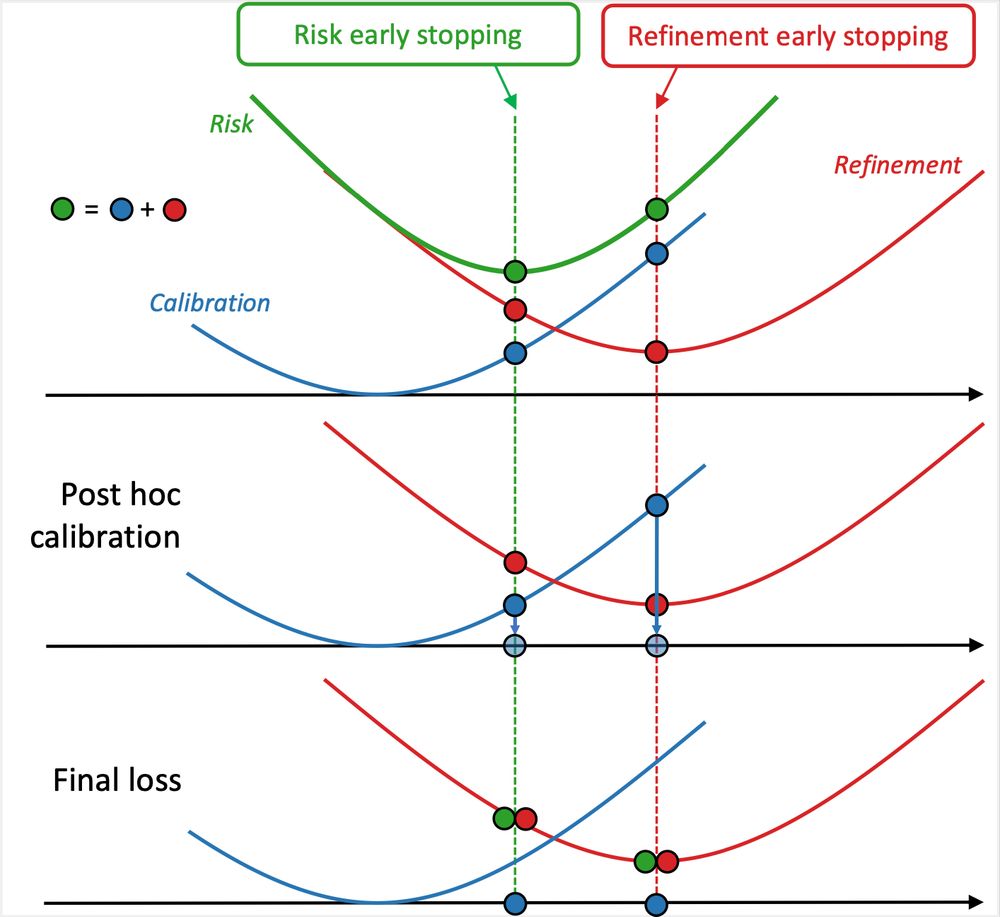
Early stopping on validation loss? This leads to suboptimal calibration and refinement errors—but you can do better!
With @dholzmueller.bsky.social, Michael I. Jordan, and @bachfrancis.bsky.social, we propose a method that integrates with any model and boosts classification performance across tasks.
With @dholzmueller.bsky.social, Michael I. Jordan, and @bachfrancis.bsky.social, we propose a method that integrates with any model and boosts classification performance across tasks.
February 3, 2025 at 1:03 PM
Early stopping on validation loss? This leads to suboptimal calibration and refinement errors—but you can do better!
With @dholzmueller.bsky.social, Michael I. Jordan, and @bachfrancis.bsky.social, we propose a method that integrates with any model and boosts classification performance across tasks.
With @dholzmueller.bsky.social, Michael I. Jordan, and @bachfrancis.bsky.social, we propose a method that integrates with any model and boosts classification performance across tasks.
Reposted by Mathieu Dagréou
Excited to see Sigmoid Attention accepted at ICLR 2025 !!
Make attention ~18% faster with a drop-in replacement 🚀
Code:
github.com/apple/ml-sig...
Paper
arxiv.org/abs/2409.04431
Make attention ~18% faster with a drop-in replacement 🚀
Code:
github.com/apple/ml-sig...
Paper
arxiv.org/abs/2409.04431

Theory, Analysis, and Best Practices for Sigmoid Self-Attention
Attention is a key part of the transformer architecture. It is a sequence-to-sequence mapping that transforms each sequence element into a weighted sum of values. The weights are typically obtained as...
arxiv.org
January 24, 2025 at 6:47 PM
Excited to see Sigmoid Attention accepted at ICLR 2025 !!
Make attention ~18% faster with a drop-in replacement 🚀
Code:
github.com/apple/ml-sig...
Paper
arxiv.org/abs/2409.04431
Make attention ~18% faster with a drop-in replacement 🚀
Code:
github.com/apple/ml-sig...
Paper
arxiv.org/abs/2409.04431
Reposted by Mathieu Dagréou
Conventional wisdom in ML is that the computation of full Jacobians and Hessians should be avoided. Instead, practitioners are advised to compute matrix-vector products, which are more in line with the inner workings of automatic differentiation (AD) backends such as PyTorch and JAX.
How to compute Hessian-vector products? | ICLR Blogposts 2024
The product between the Hessian of a function and a vector, the Hessian-vector product (HVP), is a fundamental quantity to study the variation of a function. It is ubiquitous in traditional optimizati...
iclr-blogposts.github.io
January 30, 2025 at 2:32 PM
Conventional wisdom in ML is that the computation of full Jacobians and Hessians should be avoided. Instead, practitioners are advised to compute matrix-vector products, which are more in line with the inner workings of automatic differentiation (AD) backends such as PyTorch and JAX.
Reposted by Mathieu Dagréou
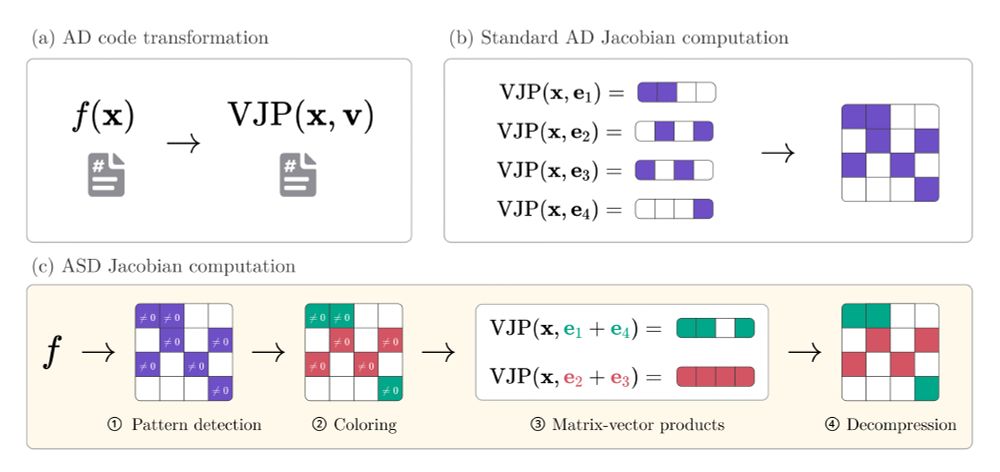
You think Jacobian and Hessian matrices are prohibitively expensive to compute on your problem? Our latest preprint with @gdalle.bsky.social might change your mind!
arxiv.org/abs/2501.17737
🧵1/8
arxiv.org/abs/2501.17737
🧵1/8
January 30, 2025 at 2:32 PM
You think Jacobian and Hessian matrices are prohibitively expensive to compute on your problem? Our latest preprint with @gdalle.bsky.social might change your mind!
arxiv.org/abs/2501.17737
🧵1/8
arxiv.org/abs/2501.17737
🧵1/8
Reposted by Mathieu Dagréou
The Mathematics of Artificial Intelligence: In this introductory and highly subjective survey, aimed at a general mathematical audience, I showcase some key theoretical concepts underlying recent advancements in machine learning. arxiv.org/abs/2501.10465

January 22, 2025 at 9:11 AM
The Mathematics of Artificial Intelligence: In this introductory and highly subjective survey, aimed at a general mathematical audience, I showcase some key theoretical concepts underlying recent advancements in machine learning. arxiv.org/abs/2501.10465
Reposted by Mathieu Dagréou
The Cheap Gradient Principle (Baur—Strassen, 1983) states that computing gradients via automatic differentiation is efficient: the gradient of a function f can be obtained with a cost proportional to evaluating f

January 16, 2025 at 6:00 AM
The Cheap Gradient Principle (Baur—Strassen, 1983) states that computing gradients via automatic differentiation is efficient: the gradient of a function f can be obtained with a cost proportional to evaluating f
Reposted by Mathieu Dagréou
The Marchenko–Pastur law describes the limiting spectral distribution of eigenvalues of large random covariance matrices. The theorem proves that as dimensions grow, the empirical spectral distribution converges weakly to this law. https://buff.ly/406Xaxg
January 22, 2025 at 6:00 AM
The Marchenko–Pastur law describes the limiting spectral distribution of eigenvalues of large random covariance matrices. The theorem proves that as dimensions grow, the empirical spectral distribution converges weakly to this law. https://buff.ly/406Xaxg
Reposted by Mathieu Dagréou
⭐️⭐️ Internship positions ⭐️⭐️
1) NLP and predictive ML to improve the management of stroke, in a multi-disciplinary and stimulating environment under the joint supervision of @adrien3000 from the @TeamHeka, me from @soda_INRIA and Eric Jouvent from @APHP team.inria.fr/soda/files/...
1) NLP and predictive ML to improve the management of stroke, in a multi-disciplinary and stimulating environment under the joint supervision of @adrien3000 from the @TeamHeka, me from @soda_INRIA and Eric Jouvent from @APHP team.inria.fr/soda/files/...
January 10, 2025 at 2:16 PM
⭐️⭐️ Internship positions ⭐️⭐️
1) NLP and predictive ML to improve the management of stroke, in a multi-disciplinary and stimulating environment under the joint supervision of @adrien3000 from the @TeamHeka, me from @soda_INRIA and Eric Jouvent from @APHP team.inria.fr/soda/files/...
1) NLP and predictive ML to improve the management of stroke, in a multi-disciplinary and stimulating environment under the joint supervision of @adrien3000 from the @TeamHeka, me from @soda_INRIA and Eric Jouvent from @APHP team.inria.fr/soda/files/...
Reposted by Mathieu Dagréou
When optimization problems have multiple minima, algorithms favor specific solutions due to their implicit bias. For ordinary least squares (OLS), gradient descent inherently converges to the minimal norm solution among all possible solutions. https://fa.bianp.net/blog/2022/implicit-bias-regression/
December 19, 2024 at 6:00 AM
When optimization problems have multiple minima, algorithms favor specific solutions due to their implicit bias. For ordinary least squares (OLS), gradient descent inherently converges to the minimal norm solution among all possible solutions. https://fa.bianp.net/blog/2022/implicit-bias-regression/

