
masker.science
I think (B) only implies (A) if the process is Markovian. So (A) appears the stronger condition.
I think (B) only implies (A) if the process is Markovian. So (A) appears the stronger condition.
Adaptive dynamics and similar are used to great effect (doi.org/10.1093/evolut/qpad042). Also phenotypic switching / plasticity, which occurs in bacteria & cancer (doi.org/10.1038/s41540-023-00309-1 + self-promo :P doi.org/10.1088/1367-2630/ad0d36). DM me for more!
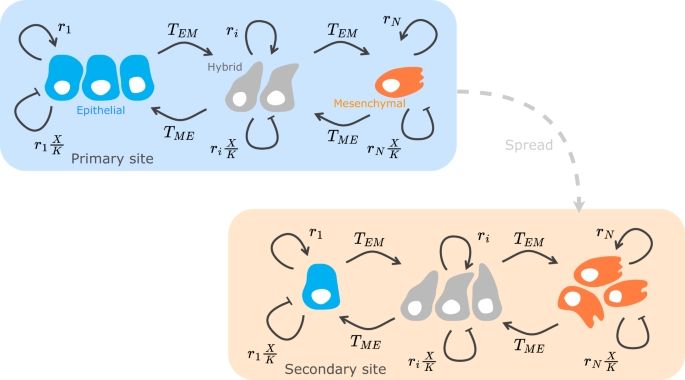
Adaptive dynamics and similar are used to great effect (doi.org/10.1093/evolut/qpad042). Also phenotypic switching / plasticity, which occurs in bacteria & cancer (doi.org/10.1038/s41540-023-00309-1 + self-promo :P doi.org/10.1088/1367-2630/ad0d36). DM me for more!


