



Other great work in this area: www.nber.org/papers/w30861, arxiv.org/abs/2501.18577, arxiv.org/abs/2411.10959, arxiv.org/abs/2306.04746 focus on “predict-then-debias”—the right move if using off the shelf data. But if you’re training the ML model yourself, give our adversarial approach a try!

Other great work in this area: www.nber.org/papers/w30861, arxiv.org/abs/2501.18577, arxiv.org/abs/2411.10959, arxiv.org/abs/2306.04746 focus on “predict-then-debias”—the right move if using off the shelf data. But if you’re training the ML model yourself, give our adversarial approach a try!
Reach out if you want to debias some measurements in a particular application!
Reach out if you want to debias some measurements in a particular application!
It’s easy to plug in any causal variable that might bias your ML-driven proxy. The adversary directly leverages your labeled data—so if you’re building custom measurement models with large-scale images (or text), you just tack on the adversary, retrain, and your bias vanishes.
8/9

It’s easy to plug in any causal variable that might bias your ML-driven proxy. The adversary directly leverages your labeled data—so if you’re building custom measurement models with large-scale images (or text), you just tack on the adversary, retrain, and your bias vanishes.
8/9
We then use a labeled forest cover data from high-resolution imagery. When comparing the ML predictions to ground-truth labels, a naive model under-estimates forest cover near roads. Our adversarial model, by contrast, recovers unbiased estimates, giving more reliable coefficients.
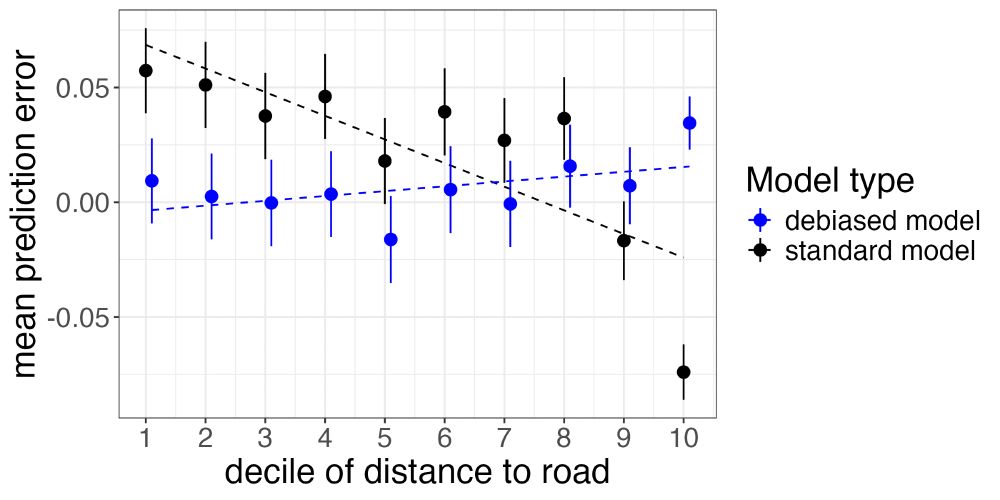
We then use a labeled forest cover data from high-resolution imagery. When comparing the ML predictions to ground-truth labels, a naive model under-estimates forest cover near roads. Our adversarial model, by contrast, recovers unbiased estimates, giving more reliable coefficients.
We induce measurement error bias in a simulation of the effect of roads on forest cover. We show that a naive model yields biased estimates of this relationship, while an adversarial model gets it right.

We induce measurement error bias in a simulation of the effect of roads on forest cover. We show that a naive model yields biased estimates of this relationship, while an adversarial model gets it right.
We also introduce a simple bias test: regress the ML prediction errors on your independent variable. If nonzero, you have measurement error bias. If you run that test while gathering ground-truth data, you can estimate how many labeled observations you’ll need to reject a target amount of bias.

We also introduce a simple bias test: regress the ML prediction errors on your independent variable. If nonzero, you have measurement error bias. If you run that test while gathering ground-truth data, you can estimate how many labeled observations you’ll need to reject a target amount of bias.
Here’s how: a primary model predicts the outcome, while an adversarial model tries to predict the treatment using the prediction errors. As the adversary learns how to predict treatment, the primary model learns to make predictions where the errors contain no information about the treatment.

Here’s how: a primary model predicts the outcome, while an adversarial model tries to predict the treatment using the prediction errors. As the adversary learns how to predict treatment, the primary model learns to make predictions where the errors contain no information about the treatment.
We are inspired by the algorithmic fairness literature. There, adversarial models force models to have balanced prediction errors across the dist. of a protected attribute (e.g. race). We adapt that approach, but instead of race, our “protected attribute” is the independent variable of interest.
We are inspired by the algorithmic fairness literature. There, adversarial models force models to have balanced prediction errors across the dist. of a protected attribute (e.g. race). We adapt that approach, but instead of race, our “protected attribute” is the independent variable of interest.

