James Bland
@jamesbland.bsky.social
Economist at UToledo. 🇦🇺 Bayesian Econometrics for economic experiments and Behavioral Economics
Free online book on this stuff here: https://jamesblandecon.github.io/StructuralBayesianTechniques/section.html
https://sites.google.com/site/jamesbland/
He/his
Free online book on this stuff here: https://jamesblandecon.github.io/StructuralBayesianTechniques/section.html
https://sites.google.com/site/jamesbland/
He/his
It's good to hear you, Gbenga! I miss you at Toledo, but I am happy you are doing important work elsewhere.
November 6, 2025 at 2:03 PM
It's good to hear you, Gbenga! I miss you at Toledo, but I am happy you are doing important work elsewhere.
This is actually SMM, not hierarchical, but it has similar flavors with unobservable heyterogeneity. I might end up using this as an example dataset in my book. Thanks for the suggestion!
November 6, 2025 at 1:35 PM
This is actually SMM, not hierarchical, but it has similar flavors with unobservable heyterogeneity. I might end up using this as an example dataset in my book. Thanks for the suggestion!
But potentially a bit of both. Some labor complements AI, other is a substitute

a little girl is asking why not both while standing in a kitchen .
ALT: a little girl is asking why not both while standing in a kitchen .
media.tenor.com
November 4, 2025 at 10:23 PM
But potentially a bit of both. Some labor complements AI, other is a substitute
(not based on much, but)
Complement in the long run. We work out better ways for humans to work with AI
Complement in the long run. We work out better ways for humans to work with AI
November 4, 2025 at 10:21 PM
(not based on much, but)
Complement in the long run. We work out better ways for humans to work with AI
Complement in the long run. We work out better ways for humans to work with AI
Fun fact: my first ever structural estimation was a QRE with unobservable Fehr-Schmit preferences. I measured how long it took by how many sets of tennis I could play before it converged.
November 4, 2025 at 9:43 PM
Fun fact: my first ever structural estimation was a QRE with unobservable Fehr-Schmit preferences. I measured how long it took by how many sets of tennis I could play before it converged.
So maybe it's fair to compare structural IO with what we do with behavioral game theory. I.e. QRE and so on. Heterogeneity in QRE gets hard very quickly, especially with unobservable, continuous types.
November 4, 2025 at 9:39 PM
So maybe it's fair to compare structural IO with what we do with behavioral game theory. I.e. QRE and so on. Heterogeneity in QRE gets hard very quickly, especially with unobservable, continuous types.
Another reason maybe that structural IO is often interested in equilibrium models. These are hard to solve even without heterogeneity. In a lot of experimental stuff, we might just have a model of optimization (i.e. no equilibrium)
November 4, 2025 at 9:39 PM
Another reason maybe that structural IO is often interested in equilibrium models. These are hard to solve even without heterogeneity. In a lot of experimental stuff, we might just have a model of optimization (i.e. no equilibrium)
There may also be issues with what each field is trying to make inference about. In experiments we often want to make inference about specific subjects, so the data augmentation you get from a BHM is really useful.
November 4, 2025 at 9:39 PM
There may also be issues with what each field is trying to make inference about. In experiments we often want to make inference about specific subjects, so the data augmentation you get from a BHM is really useful.
Interesting. It seems to me (and I might be a bit biased here) that structural for experiments is moving toward Bayesian hierarchical modeling, which is really different to SMM in terms of identification strategy. You have to specify the full likelihood, for one thing.
November 4, 2025 at 9:39 PM
Interesting. It seems to me (and I might be a bit biased here) that structural for experiments is moving toward Bayesian hierarchical modeling, which is really different to SMM in terms of identification strategy. You have to specify the full likelihood, for one thing.
And of course, this paper would be really useless without some example code, so here you go:
github.com/JamesBlandEc...
github.com/JamesBlandEc...

GitHub - JamesBlandEcon/HeterogeneityForThePractitioner: Code for "Adding parameter heterogeneity to structural models: some guidance for the practitioner"
Code for "Adding parameter heterogeneity to structural models: some guidance for the practitioner" - JamesBlandEcon/HeterogeneityForThePractitioner
github.com
November 4, 2025 at 4:42 PM
And of course, this paper would be really useless without some example code, so here you go:
github.com/JamesBlandEc...
github.com/JamesBlandEc...
So there you have it. Four ways of modeling the heterogeneity. These aren't mutually exclusive, for example you could have a hierarchical model where the population means are a function of participant demographics.
November 4, 2025 at 4:42 PM
So there you have it. Four ways of modeling the heterogeneity. These aren't mutually exclusive, for example you could have a hierarchical model where the population means are a function of participant demographics.
Or you could estimate a hierarchical model that assumes your participants' parameters are drawn from a population distribution.


November 4, 2025 at 4:42 PM
Or you could estimate a hierarchical model that assumes your participants' parameters are drawn from a population distribution.
Or you could assume a finite mixture of preference types
I really don't like this one, especially for this application. It really looks more like a continuous distribution.
I really don't like this one, especially for this application. It really looks more like a continuous distribution.

November 4, 2025 at 4:42 PM
Or you could assume a finite mixture of preference types
I really don't like this one, especially for this application. It really looks more like a continuous distribution.
I really don't like this one, especially for this application. It really looks more like a continuous distribution.
Now come some "in between" choices.
If you have participant demographics, you can make your parameters a function of these
If you have participant demographics, you can make your parameters a function of these

November 4, 2025 at 4:42 PM
Now come some "in between" choices.
If you have participant demographics, you can make your parameters a function of these
If you have participant demographics, you can make your parameters a function of these
At the other end of things, you can estimate your model once for every participant. This is really flexible, but your estimates will likely be imprecise.

November 4, 2025 at 4:42 PM
At the other end of things, you can estimate your model once for every participant. This is really flexible, but your estimates will likely be imprecise.
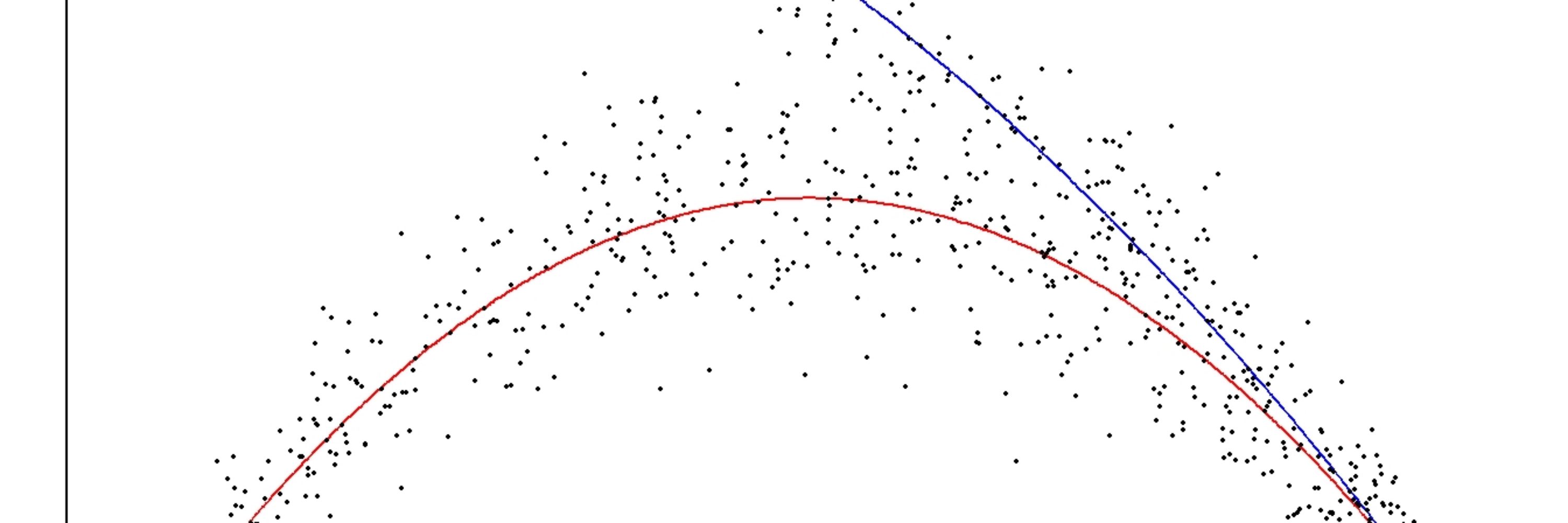
First (not advisable) you can ignore the heterogeneity and assume everyone is the same.
Simple, easy, probably very wrong.
Simple, easy, probably very wrong.

November 4, 2025 at 4:42 PM
First (not advisable) you can ignore the heterogeneity and assume everyone is the same.
Simple, easy, probably very wrong.
Simple, easy, probably very wrong.
Big idea: I want to estimate a structural model, and I suspect my participants are heterogeneous. What can I do? I discuss some approaches you might want to think about
November 4, 2025 at 4:42 PM
Big idea: I want to estimate a structural model, and I suspect my participants are heterogeneous. What can I do? I discuss some approaches you might want to think about
But you're more of a comment
October 30, 2025 at 6:39 PM
But you're more of a comment
In a common experiment design, I show that RDU preferences can be nonconvex. This can be a problem for estimation, as there can be multiple optima.

October 27, 2025 at 6:31 PM
In a common experiment design, I show that RDU preferences can be nonconvex. This can be a problem for estimation, as there can be multiple optima.

