yes, it does raise questions (and I don't have an answer yet). but I am not sure whether the practical setting falls within the smooth case neither (if smooth=Lipschitz smooth; and even if smooth=differentiable, there are non-diff elements in the architecture like RMSNorm)

This is joint work with @haeggee.bsky.social, Adrien Taylor, Umut Simsekli and @bachfrancis.bsky.social

🗞️ arxiv.org/abs/2501.18965

🔦 github.com/fabian-sp/lr...

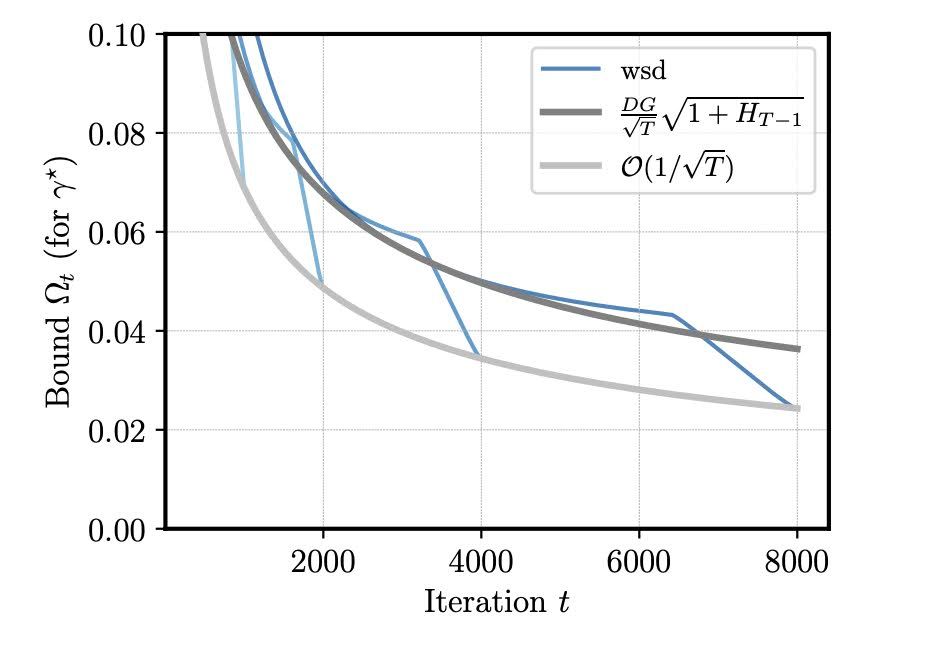
Bonus: this provides a provable explanation for the benefit of cooldown: if we plug in the wsd schedule into the bound, a log-term (H_T+1) vanishes compared to constant LR (dark grey).

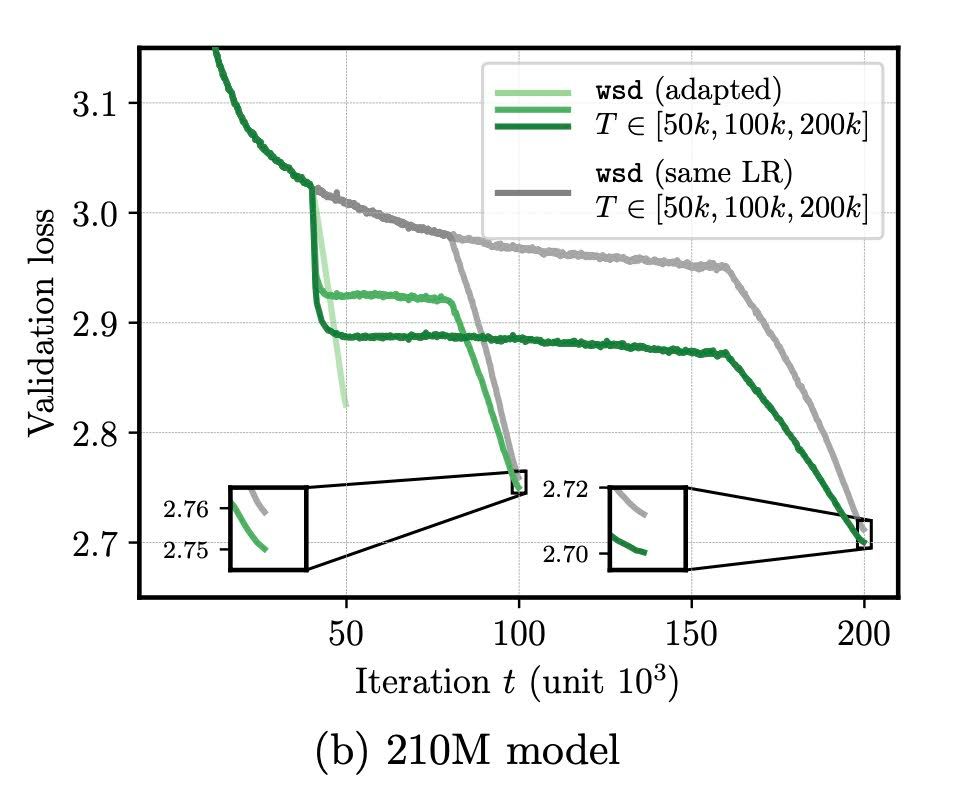
How does this help in practice? In continued training, we need to decrease the learning rate in the second phase. But by how much?

Using the theoretically optimal schedule (which can be computed for free), we obtain noticeable improvement in training 124M and 210M models.

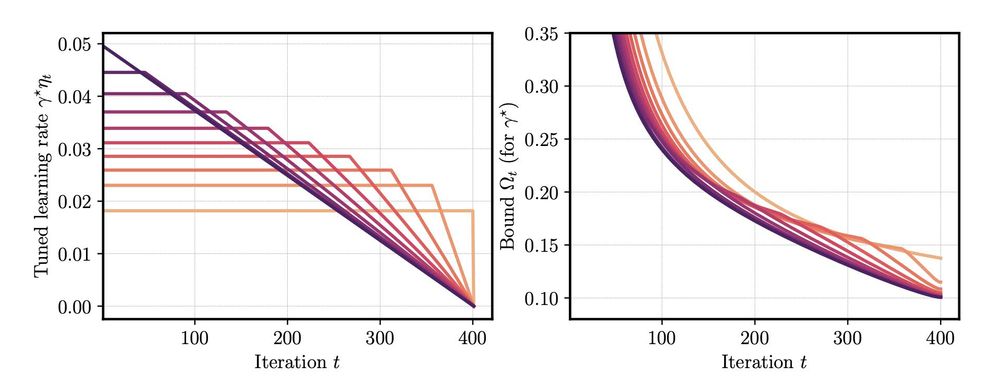
This allows to understand LR schedules beyond experiments: we study (i) optimal cooldown length, (ii) the impact of gradient norm on the schedule performance.
The second part suggests that the sudden drop in loss during cooldown happens when gradient norms do not go to zero.

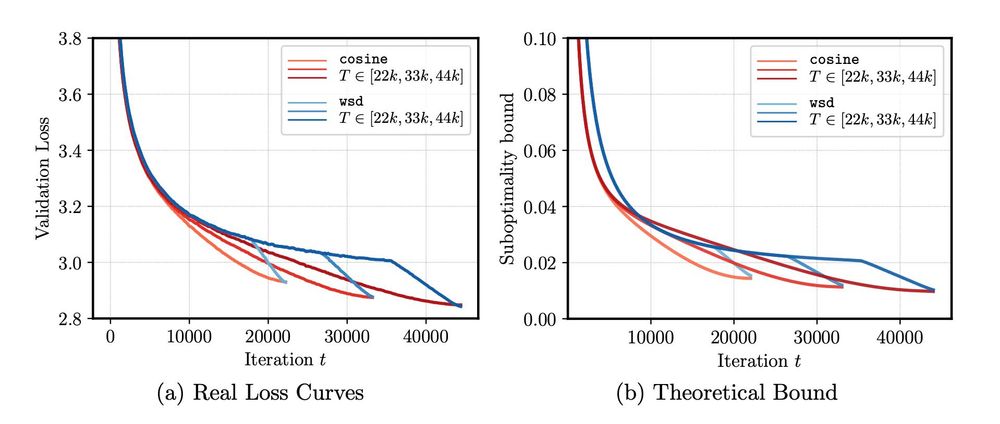
Using a bound from arxiv.org/pdf/2310.07831, we can reproduce the empirical behaviour of cosine and wsd (=constant+cooldown) schedule. Surprisingly the result is for convex problems, but still matches the actual loss of (nonconvex) LLM training.

nice!
Figure 9 looks like a lighthouse guiding the way (towards the data distribution)

you could run an online method for the quantile problem? sth similar to the online median arxiv.org/abs/2402.12828

could you add me? ✌🏻

would love to be added :)