
https://www.ehkennedy.com/
interested in causality, machine learning, nonparametrics, public policy, etc
Pfanzagl gives this 1-step estimator here - in causal inference this is exactly the doubly robust / DML estimator you know & love!



Pfanzagl gives this 1-step estimator here - in causal inference this is exactly the doubly robust / DML estimator you know & love!
Richard von Mises first characterized smoothness this way for stats in the 30s/40s! eg:
projecteuclid.org/journals/ann...


Richard von Mises first characterized smoothness this way for stats in the 30s/40s! eg:
projecteuclid.org/journals/ann...
But the reality is that observational methods are used everyday to answer pressing causal questions that cannot be studied in randomized trials."
- Jamie Robins, 2002
tinyurl.com/4yuxfxes
tinyurl.com/zncp39mr


But the reality is that observational methods are used everyday to answer pressing causal questions that cannot be studied in randomized trials."
- Jamie Robins, 2002
tinyurl.com/4yuxfxes
tinyurl.com/zncp39mr
Why not both?
Here we propose novel hybrid smooth+agnostic model, give minimax rates, & new optimal methods
arxiv.org/pdf/2405.08525
-> fast rates under weaker conditions




Why not both?
Here we propose novel hybrid smooth+agnostic model, give minimax rates, & new optimal methods
arxiv.org/pdf/2405.08525
-> fast rates under weaker conditions
Led by amazing postdoc Alex Levis: www.awlevis.com/about/
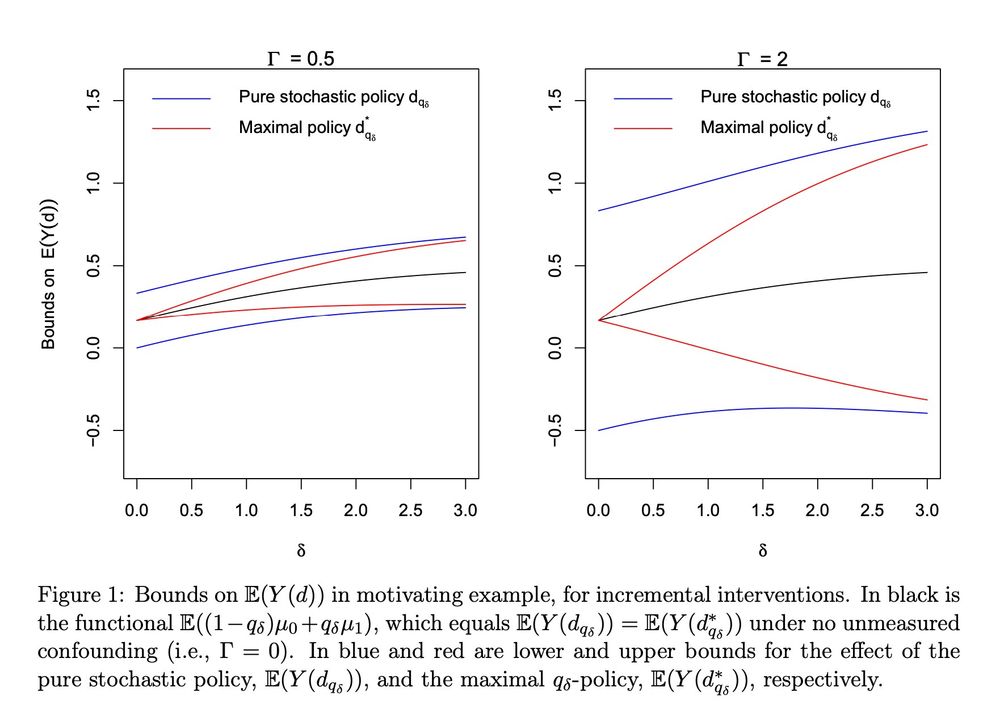
We show causal effects of new "soft" interventions are less sensitive to unmeasured confounding
& study which effects are *least* sensitive to confounding -> makes new connections to optimal transport



Led by amazing postdoc Alex Levis: www.awlevis.com/about/
We show causal effects of new "soft" interventions are less sensitive to unmeasured confounding
& study which effects are *least* sensitive to confounding -> makes new connections to optimal transport
arxiv.org/abs/2409.11967
i.e., soft interventions on cts treatments like dose, duration, frequency
it turns out exponential tilts preserve all nice properties of incremental effects with binary trt (arxiv.org/abs/1704.00211)




arxiv.org/abs/2409.11967
i.e., soft interventions on cts treatments like dose, duration, frequency
it turns out exponential tilts preserve all nice properties of incremental effects with binary trt (arxiv.org/abs/1704.00211)
arxiv.org/abs/2305.04116
We study if one can improve popular semiparametric / doubly robust / DML causal effect estimators - w/o adding structural assumptions...
Short answer: nope!
Turns out these methods are minimax optimal here
www.ehkennedy.com/uploads/5/8/...




arxiv.org/abs/2305.04116
We study if one can improve popular semiparametric / doubly robust / DML causal effect estimators - w/o adding structural assumptions...
Short answer: nope!
Turns out these methods are minimax optimal here
www.ehkennedy.com/uploads/5/8/...
check out this talk by Siva Balakrishnan for an excellent & comprehensive summary of the state of the art
www.youtube.com/live/Mnum0Ox...
www.stat.cmu.edu/~siva/




check out this talk by Siva Balakrishnan for an excellent & comprehensive summary of the state of the art
www.youtube.com/live/Mnum0Ox...
www.stat.cmu.edu/~siva/


Here is an estimator from a 1982 textbook that today would be called double machine learning or something similar

Here is an estimator from a 1982 textbook that today would be called double machine learning or something similar
Even throws in a mention of sample-splitting / cross-fitting! (from Hasminskii & Ibragimov 1979)



Even throws in a mention of sample-splitting / cross-fitting! (from Hasminskii & Ibragimov 1979)
Pfanzagl gives this 1-step estimator here - in causal inference this is exactly the doubly robust / DML estimator you know & love!



Pfanzagl gives this 1-step estimator here - in causal inference this is exactly the doubly robust / DML estimator you know & love!
I note this in my tutorial here:
x.com/edwardhkenne...
Also v related to neyman orthogonality - worth a separate thread



I note this in my tutorial here:
x.com/edwardhkenne...
Also v related to neyman orthogonality - worth a separate thread
Richard von Mises first characterized smoothness this way for stats in the 30s/40s! eg:
projecteuclid.org/euclid.aoms/...


Richard von Mises first characterized smoothness this way for stats in the 30s/40s! eg:
projecteuclid.org/euclid.aoms/...
projecteuclid.org/euclid.aos/1...
A more detailed discussion of the early days is in the comprehensive semiparametrics text by BKRW:
springer.com/gp/book/9780...
Would love to hear if others know good historical resources!


projecteuclid.org/euclid.aos/1...
A more detailed discussion of the early days is in the comprehensive semiparametrics text by BKRW:
springer.com/gp/book/9780...
Would love to hear if others know good historical resources!
jiayinggu.weebly.com/uploads/3/8/...
"Why does it take so long? Why haven't I done ten times as much as I have? Why do I bother over & over again trying the wrong way when the right way was staring me in the face all the time? I don't know."



jiayinggu.weebly.com/uploads/3/8/...
"Why does it take so long? Why haven't I done ten times as much as I have? Why do I bother over & over again trying the wrong way when the right way was staring me in the face all the time? I don't know."

Superb example of how to tell a story including average effects, heterogeneous effects, & sensitivity analysis (i.e., relaxing assumptions abt confounding)




Superb example of how to tell a story including average effects, heterogeneous effects, & sensitivity analysis (i.e., relaxing assumptions abt confounding)



- Larry Wasserman #statsquotes
www.jstor.org/stable/26699...

- Larry Wasserman #statsquotes
www.jstor.org/stable/26699...
github.com/matteobonvin...
Paper:
arxiv.org/abs/1912.02793


github.com/matteobonvin...
Paper:
arxiv.org/abs/1912.02793
There are lots of different kinds of sensitivity analysis models - the Cinelli & Hazlett one is more specialized/structured, & assumes more.
The lit review in this paper might be useful:
arxiv.org/pdf/2104.083...

There are lots of different kinds of sensitivity analysis models - the Cinelli & Hazlett one is more specialized/structured, & assumes more.
The lit review in this paper might be useful:
arxiv.org/pdf/2104.083...






