
David Bessis
@davidbessis.bsky.social
Rogue mathematician
https://davidbessis.substack.com/
https://davidbessis.substack.com/
Another notable omission is Poincaré. I'm more embarrassed about this one, as I hadn't done my homework and should have read him more early in the writing process — but reading him at the end of the process provided validation and reassurance.
November 7, 2025 at 4:56 AM
Another notable omission is Poincaré. I'm more embarrassed about this one, as I hadn't done my homework and should have read him more early in the writing process — but reading him at the end of the process provided validation and reassurance.
As for Thom, he clearly influenced me (as I read a lot about catastrophe theory in my early 20s) but not through his philosophical writings and not in a way I can easily convey. Again, I wanted to write an accessible book, not a reference-complete one.
November 7, 2025 at 4:56 AM
As for Thom, he clearly influenced me (as I read a lot about catastrophe theory in my early 20s) but not through his philosophical writings and not in a way I can easily convey. Again, I wanted to write an accessible book, not a reference-complete one.
Thanks! Re Holton and Bachelard: I never the read the former, and only read the latter during the book writing process (as a friend suggested I should) and decided not include him, because it wouldn't have added incremental clarity and I didn't want to write an "erudite" book.
November 7, 2025 at 4:56 AM
Thanks! Re Holton and Bachelard: I never the read the former, and only read the latter during the book writing process (as a friend suggested I should) and decided not include him, because it wouldn't have added incremental clarity and I didn't want to write an "erudite" book.
You overestimate me :)
March 28, 2025 at 7:46 AM
You overestimate me :)
@truerphilosophy.bsky.social: for what it's worth, your post is getting massively more views and likes on another site ;)
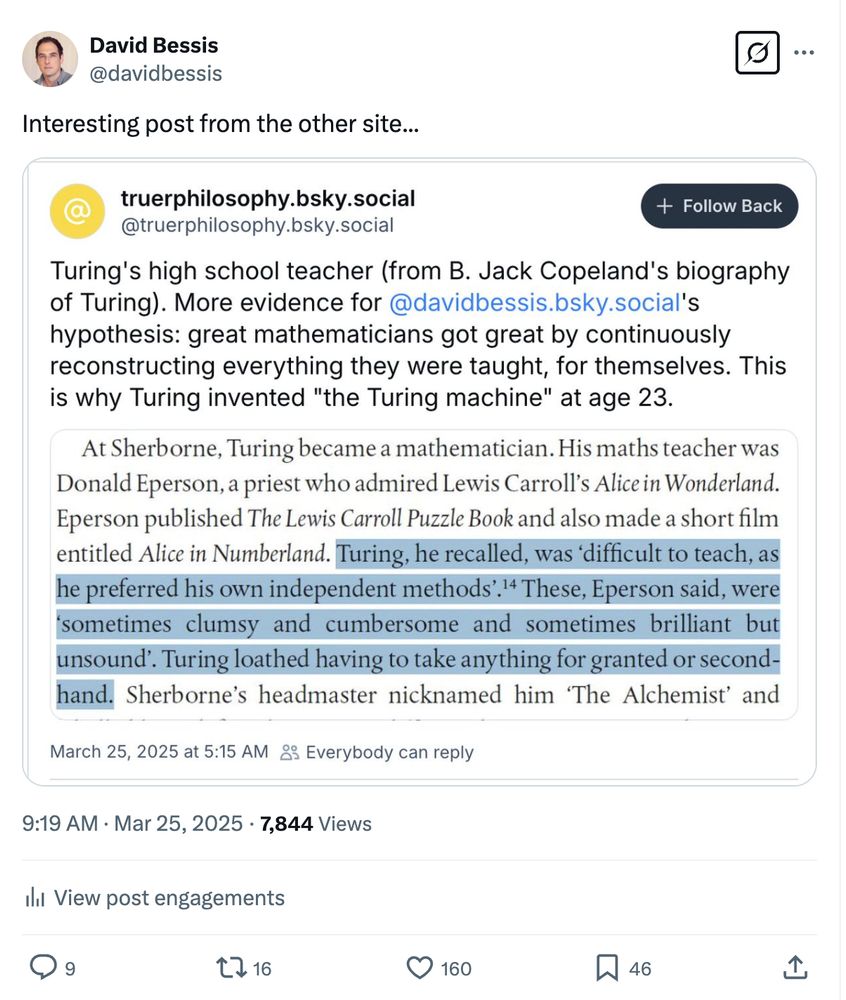
March 25, 2025 at 6:27 PM
@truerphilosophy.bsky.social: for what it's worth, your post is getting massively more views and likes on another site ;)
There's absolutely a case for a "formalization" of math research output. It is will happen. The process has started with Lean and is unstoppable, because the community *needs* it.
[Says the guy who submitted a 100 paper that took 7 years to review and get accepted by the Annals of Mathematics.]
[Says the guy who submitted a 100 paper that took 7 years to review and get accepted by the Annals of Mathematics.]
January 24, 2025 at 6:12 AM
There's absolutely a case for a "formalization" of math research output. It is will happen. The process has started with Lean and is unstoppable, because the community *needs* it.
[Says the guy who submitted a 100 paper that took 7 years to review and get accepted by the Annals of Mathematics.]
[Says the guy who submitted a 100 paper that took 7 years to review and get accepted by the Annals of Mathematics.]
Reposted by David Bessis
So:
- concrete foundations for formal math
- sand and mud foundations for intuitive math
- no reason to do formal math if it wasn't for its "meaning"
=> math only exists because meaningless formalism ENHANCES our ability to build semantics
=> this is the true motivation of my conceptualist take
- concrete foundations for formal math
- sand and mud foundations for intuitive math
- no reason to do formal math if it wasn't for its "meaning"
=> math only exists because meaningless formalism ENHANCES our ability to build semantics
=> this is the true motivation of my conceptualist take
January 23, 2025 at 11:59 AM
So:
- concrete foundations for formal math
- sand and mud foundations for intuitive math
- no reason to do formal math if it wasn't for its "meaning"
=> math only exists because meaningless formalism ENHANCES our ability to build semantics
=> this is the true motivation of my conceptualist take
- concrete foundations for formal math
- sand and mud foundations for intuitive math
- no reason to do formal math if it wasn't for its "meaning"
=> math only exists because meaningless formalism ENHANCES our ability to build semantics
=> this is the true motivation of my conceptualist take
So:
- concrete foundations for formal math
- sand and mud foundations for intuitive math
- no reason to do formal math if it wasn't for its "meaning"
=> math only exists because meaningless formalism ENHANCES our ability to build semantics
=> this is the true motivation of my conceptualist take
- concrete foundations for formal math
- sand and mud foundations for intuitive math
- no reason to do formal math if it wasn't for its "meaning"
=> math only exists because meaningless formalism ENHANCES our ability to build semantics
=> this is the true motivation of my conceptualist take
January 23, 2025 at 11:59 AM
So:
- concrete foundations for formal math
- sand and mud foundations for intuitive math
- no reason to do formal math if it wasn't for its "meaning"
=> math only exists because meaningless formalism ENHANCES our ability to build semantics
=> this is the true motivation of my conceptualist take
- concrete foundations for formal math
- sand and mud foundations for intuitive math
- no reason to do formal math if it wasn't for its "meaning"
=> math only exists because meaningless formalism ENHANCES our ability to build semantics
=> this is the true motivation of my conceptualist take
My next substack post should be on why logical formalism can't account for the "semantic" aspect of math, which is the key issue at stake here. The practical semantics of math comes from human cognition, not formalism itself.
January 23, 2025 at 11:55 AM
My next substack post should be on why logical formalism can't account for the "semantic" aspect of math, which is the key issue at stake here. The practical semantics of math comes from human cognition, not formalism itself.
... which is mostly true, in the sense that, with Lean, there will eventually be a convergence.
So, in a way, the "official language of mathematics" might be something like Lean.
So, in a way, the "official language of mathematics" might be something like Lean.
January 23, 2025 at 11:55 AM
... which is mostly true, in the sense that, with Lean, there will eventually be a convergence.
So, in a way, the "official language of mathematics" might be something like Lean.
So, in a way, the "official language of mathematics" might be something like Lean.

