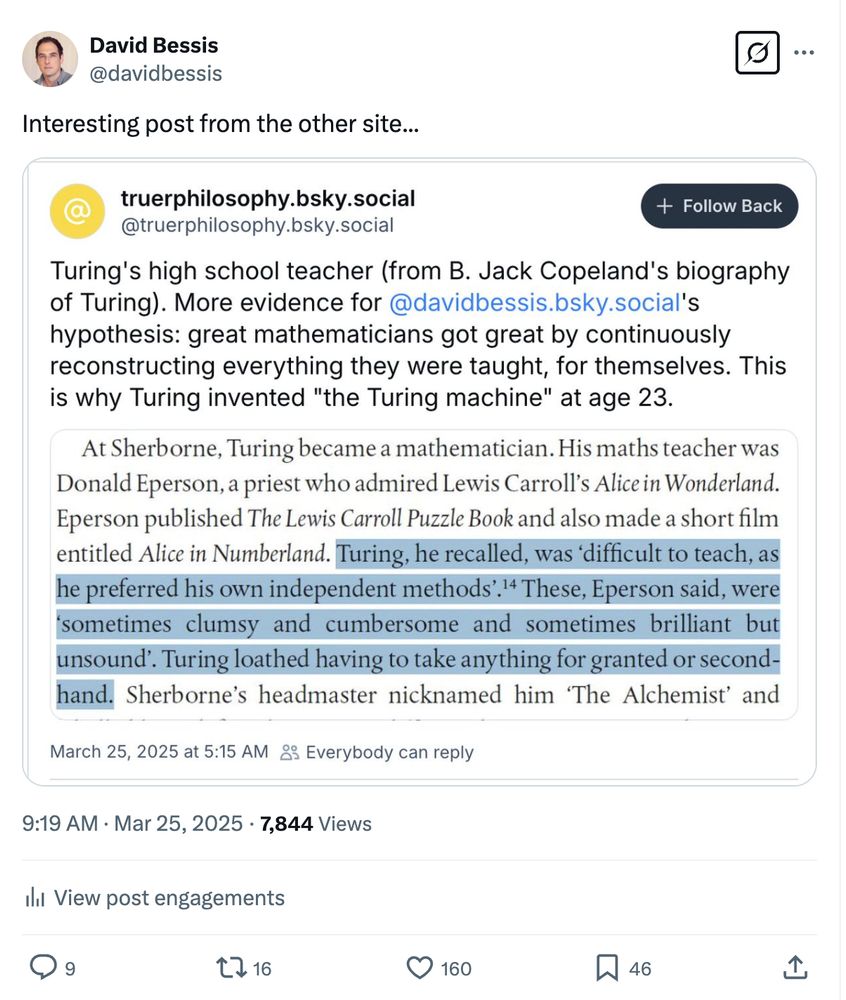
@truerphilosophy.bsky.social: for what it's worth, your post is getting massively more views and likes on another site ;)

For some reason, my first long form post is suddenly getting viral: it received 2x more views in the past 30 days than in the first 3 months.
davidbessis.substack.com/p/weve-been-...

Beauty.

The fascinating final words of Bouchard's 1990 Science paper on IQ & twins reared apart.
While the paper is methodologically unsound — and its results aren't to be trusted — I actually enjoy the boldness of their conclusion.
Make no mistake, the stakes are super high!

❤️❤️❤️

Philosophers: logic is the foundation of mathematics.

Mathematicians:

Wow, look at who's tweeting about my book 🥰!
x.com/AlbertEinste...

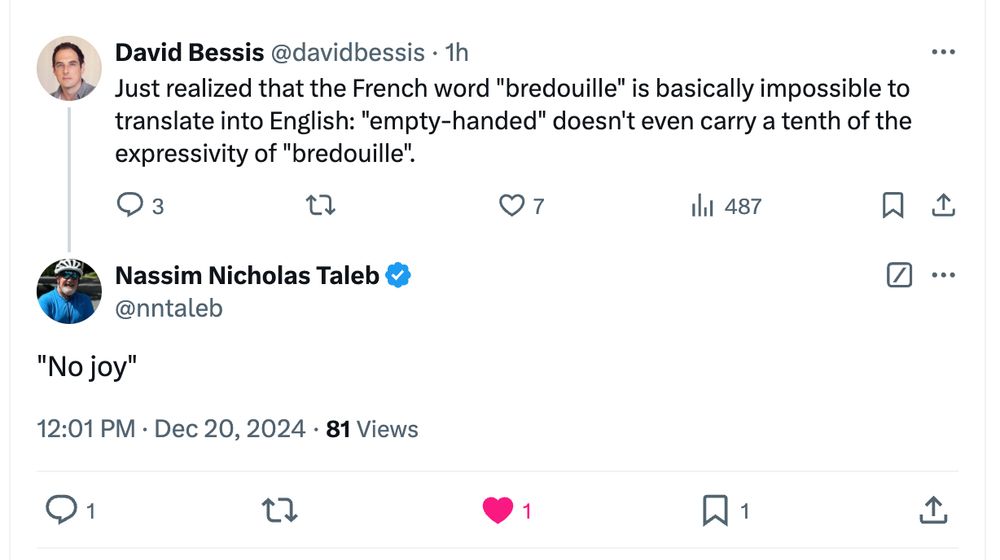
Twitter/X still has a clear advantage over Bluesky: you can get quick replies like this one.

Le dernier chapitre a été substantiellement amélioré dans l'édition US, et se termine sur cette phrase : "Now that we're teaching machines the secrets of intelligence, it's about time we start teaching humans."

My coauthor is a ghost.

Damn, I made an incorrect statement in Chapter 2 of Mathematica: some people *do hate* spoons.
But this validates the core lesson from Chapter 18: outside of mathematics, there's no such thing as absolute truth.

Second lifetime achievement of the week:
have a Fields medallist comment on your LinkedIn post ✅

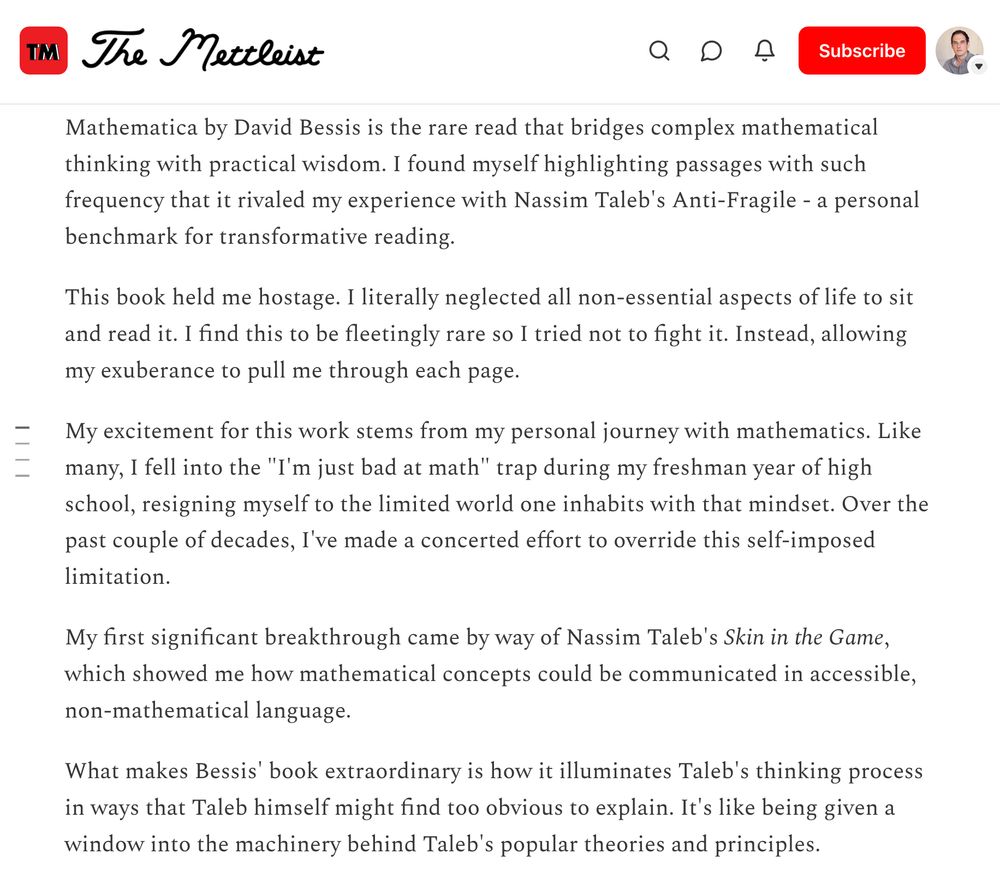
"This book held me hostage", "I found myself highlighting passages with such frequency that it rivalled my experience with Nassim Taleb's Antifragile — a personal benchmark for transformative reading."
A great review of Mathematica by Andrew Pennachio:
www.themettleist.com/p/mathematic...

All that was easy compared to getting the paper accepted by the Annals of Math. The first 3 referees gave up, complaining that the paper was too hard. It was only saved by the 4th referee. The entire refereeing process took nearly 7 years.

17/17

The conjecture wasn’t yet fully proven, but I had made major progress and only one possible exception remained, G31. I addressed it 18 months later with a second creative burst that lasted 6 weeks (which is described in Chapter 16 of my book.)

11/17

There was one big conjecture central to my field of study: the 𝐾(𝜋,1) conjecture for finite complex reflection groups. The case of complexified real groups had famously been solved by Deligne in 1972, but very little progress had been made since then.

4/17

How I woke up one day and decided to solve a math conjecture from the 1970s...

1/17

"Mathematica, a Secret World of Intuition and Curiosity" is out today — phew! It took me 20 years to fail to write it and 1 to actually write it.
In a nutshell: it's a book about what actually goes on inside a mathematician's head, blurbed by Fields medallists.
yalebooks.yale.edu/book/9780300...

The paper's introduction makes this interesting comment about IQ heritability: one could challenge that it's around 0.75, but a lower value would still allow Jensen to make his argument, so they're not going to fight this battle.
This echoes your 2015 comment that had prompted my question... /2