
🥷stealth-mode CEO
🔬prev visiting @ Cambridge | RS intern @ Amazon Search | RS intern @ Alexa.
🆓 time 🎭improv theater, 🤿scuba diving, ⛰️hiking
This leads to an impressive +15% gain without any test-time adaptation!
The improvement is consistent across all datasets.
🧵(5/6)
This leads to an impressive +15% gain without any test-time adaptation!
The improvement is consistent across all datasets.
🧵(5/6)
(B) This interference is higher in shallower (more general) layers and lower in deeper (more task-specific) layers!
🧵(4/6)

(B) This interference is higher in shallower (more general) layers and lower in deeper (more task-specific) layers!
🧵(4/6)
The answer is NO! In fact, it can even be detrimental.
Why is that?
🧵(3/6)

The answer is NO! In fact, it can even be detrimental.
Why is that?
🧵(3/6)
By keeping only a small fraction (e.g., 10%) of task singular vectors for each model, average accuracy is preserved!
🧵(2/6)

By keeping only a small fraction (e.g., 10%) of task singular vectors for each model, average accuracy is preserved!
🧵(2/6)
1. Perform a low-rank approximation of layer-wise task vectors.
2. Minimize task interference by orthogonalizing inter-task singular vectors.
🧵(1/6)
1. Perform a low-rank approximation of layer-wise task vectors.
2. Minimize task interference by orthogonalizing inter-task singular vectors.
🧵(1/6)
The approach is designed to merge 3+ models (as CC doesn't make much sense otherwise), but if you are curious about applying Frank-Wolfe for n=2, please check the paper!
(5/6)

The approach is designed to merge 3+ models (as CC doesn't make much sense otherwise), but if you are curious about applying Frank-Wolfe for n=2, please check the paper!
(5/6)
1) Optimizing globally, we don't have any more variance from the random layer order
2) The models in the universe are much more linearly connected than before
3) The models in the universe are much more similar
Does this result in better merging?
(4/6)

1) Optimizing globally, we don't have any more variance from the random layer order
2) The models in the universe are much more linearly connected than before
3) The models in the universe are much more similar
Does this result in better merging?
(4/6)
1) Start from the weight-matching equation introduced by Git Re-Basin
2) Consider perms between all possible pairs
3) Replace each permutation A->B with one mapping to the universe A -> U and one mapping back U -> B
4) Optimize with Frank-Wolfe
(3/6)

1) Start from the weight-matching equation introduced by Git Re-Basin
2) Consider perms between all possible pairs
3) Replace each permutation A->B with one mapping to the universe A -> U and one mapping back U -> B
4) Optimize with Frank-Wolfe
(3/6)
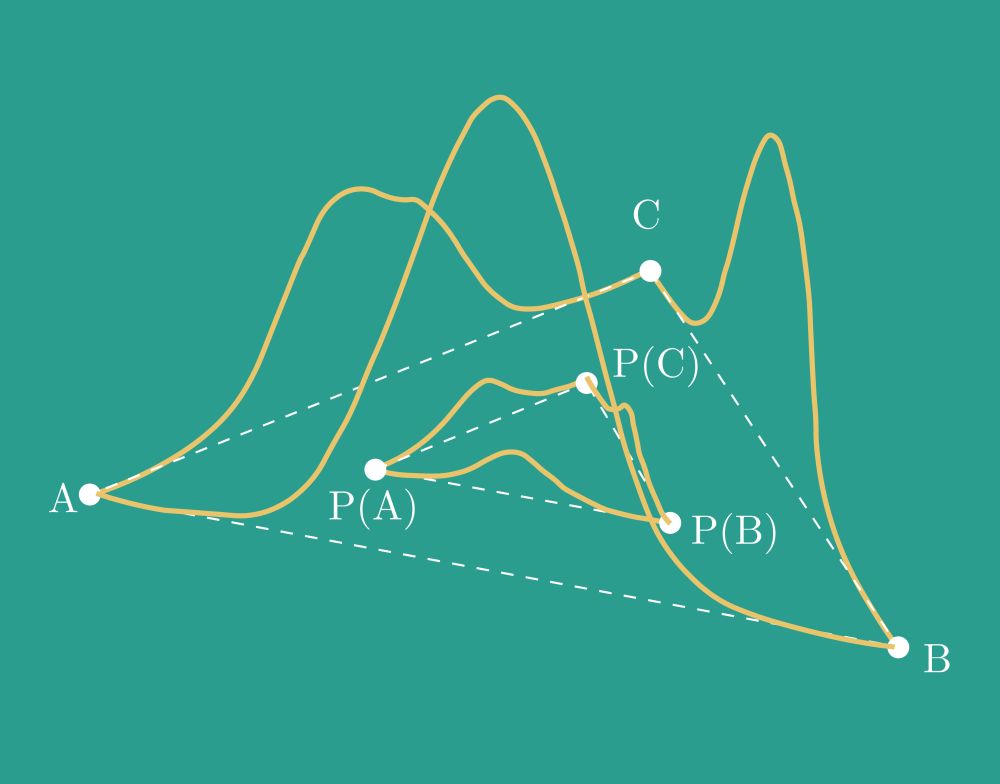
What then? Introduce a Universe space 🌌and use it as a midpoint 🔀
This way, CC is guaranteed!
(2/6)

What then? Introduce a Universe space 🌌and use it as a midpoint 🔀
This way, CC is guaranteed!
(2/6)
Say no more!
It just so happens that our new #NeurIPS24 paper covers exactly this!
Huh? No idea what I am talking about? Read on
(1/6)
Say no more!
It just so happens that our new #NeurIPS24 paper covers exactly this!
Huh? No idea what I am talking about? Read on
(1/6)

