
Il vaut mieux utiliser les polynômes d'interpolation de Lagrange, en fait.

Il vaut mieux utiliser les polynômes d'interpolation de Lagrange, en fait.
Pour l'instant je gribouille...
I've completed Part One of "Crossed Wires" - Day 24 - Advent of Code 2024 adventofcode.com/2024/day/24 #AdventOfCode

Pour l'instant je gribouille...
I've completed Part One of "Crossed Wires" - Day 24 - Advent of Code 2024 adventofcode.com/2024/day/24 #AdventOfCode
6.5 secondes.
(code en alt-text)
![def f(x) :
y = (x ^ (64*x) ) % 16777216
z = (y // 32 ^ y) % 16777216
t = (z * 2048 ^ z) % 16777216
return t
def toSeq(val) :
a,b,c,d,e = val
return (b-a,c-b,d-c,e-d)
def init(x) :
l = []
for k in range(4) :
l.append(x%10)
x = f(x)
return x,tuple(l+[x%10])
scores = {}
dM = 2000
def calculerSuite(x) :
vis = {}
x,val = init(x)
for k in range(dM-4) :
code = toSeq(val)
if not code in vis :
if not code in scores :
scores[code] = 0
vis[code] = 1
scores[code] += val[-1]
x = f(x)
val = val[1:] + (x%10,)
return
for i,x in enumerate(inputs) :
calculerSuite(x)
print(max([scores[x] for x in scores]))](https://cdn.bsky.app/img/feed_thumbnail/plain/did:plc:fibit7sncdk6et4elpylfqvl/bafkreiax3iky3i5ytr3epwpbeusnf3msvb3ni2hwhc5nnpiw5cm5tiukiq@jpeg)
6.5 secondes.
(code en alt-text)
Des séquences qui sont effectivement susceptibles d'apparaître, il y en a bien 40951.
Une séquence comme (3,3,3,3) ne peut pas apparaître avec des chiffres de 0 à 9 par exemple.

Des séquences qui sont effectivement susceptibles d'apparaître, il y en a bien 40951.
Une séquence comme (3,3,3,3) ne peut pas apparaître avec des chiffres de 0 à 9 par exemple.



Tu frimes un peu, là !
Je propose la méthode doable2 qui est 100 fois plus rapide.

Tu frimes un peu, là !
Je propose la méthode doable2 qui est 100 fois plus rapide.
Tant que A est non nul, remplacer A par f(A) et retourner B.
(interprétée avec mes yeux et mes doigts)
Chaque tour de la boucle dépend des 10 derniers bits de A, et détruit les 3 derniers bits de A.

Tant que A est non nul, remplacer A par f(A) et retourner B.
(interprétée avec mes yeux et mes doigts)
Chaque tour de la boucle dépend des 10 derniers bits de A, et détruit les 3 derniers bits de A.
Bien vu !
Chacun sait en effet que la première étape de l'ébeniste est la contemplation de l'idée abstraite, immatérielle et unique de ✨LIT💫 avant de se mettre au travail.
Ensuite, c'est le peintre qui prend le relais.

Bien vu !
Chacun sait en effet que la première étape de l'ébeniste est la contemplation de l'idée abstraite, immatérielle et unique de ✨LIT💫 avant de se mettre au travail.
Ensuite, c'est le peintre qui prend le relais.
Ce que tu détestes, c'est ton manque de maths quand il t'en faudrait.


Ce que tu détestes, c'est ton manque de maths quand il t'en faudrait.
Je suis maintenant l'heureux propriétaire d'un fichier texte de 105 Mo dans lequel il y a quelque part un très joli sapin !
I just completed "Restroom Redoubt" - Day 14 - Advent of Code 2024 #AdventOfCode adventofcode.com/2024/day/14

Je suis maintenant l'heureux propriétaire d'un fichier texte de 105 Mo dans lequel il y a quelque part un très joli sapin !
I just completed "Restroom Redoubt" - Day 14 - Advent of Code 2024 #AdventOfCode adventofcode.com/2024/day/14
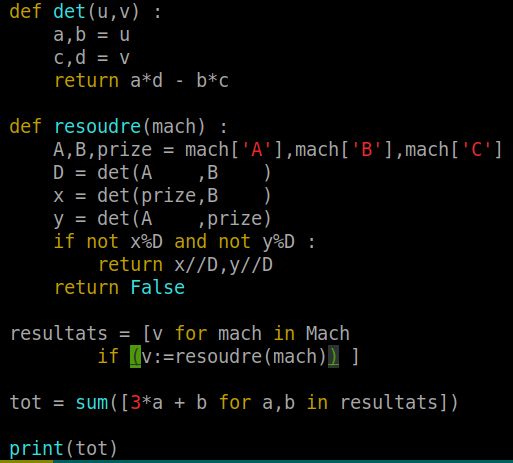
Première fois de ma vie que j'arrive à faire un Walrus qui fonctionne ! 😋
(Apparemment, c'est les parenthèses random qui permettent le truc sinon, message d'erreur !)

Première fois de ma vie que j'arrive à faire un Walrus qui fonctionne ! 😋
(Apparemment, c'est les parenthèses random qui permettent le truc sinon, message d'erreur !)
(un post sur Reddit fait remarquer qu'il n'y a pas de raison de faire l'acquisition programmatiquement, et qu'on peut très bien la faire dans son éditeur de texte favori !)


(un post sur Reddit fait remarquer qu'il n'y a pas de raison de faire l'acquisition programmatiquement, et qu'on peut très bien la faire dans son éditeur de texte favori !)

Finalement, j'ai fait un dictionnaire de fonctions.
Je pense que ça revient un peu au même qu'un match case.

Finalement, j'ai fait un dictionnaire de fonctions.
Je pense que ça revient un peu au même qu'un match case.

Je viens de faire le jour 5.
Je crois que ce serait bien de ré-usiner le code avant de passer à la suite ! 😅


Je viens de faire le jour 5.
Je crois que ce serait bien de ré-usiner le code avant de passer à la suite ! 😅
Quel petit menteur ! 😅
Il n'a des données que jusqu'à septembre 2021, mais sait que c'est le problème du 8 décembre 2021.

Quel petit menteur ! 😅
Il n'a des données que jusqu'à septembre 2021, mais sait que c'est le problème du 8 décembre 2021.
(bon, après, c'est un problème de 2021, peut-être qu'il le connaissait déjà explicitement !)

(bon, après, c'est un problème de 2021, peut-être qu'il le connaissait déjà explicitement !)
Chaudement recommandé.
I've completed "Seven Segment Search" - Day 8 - Advent of Code 2021 adventofcode.com/2021/day/8 #AdventOfCode

Chaudement recommandé.
I've completed "Seven Segment Search" - Day 8 - Advent of Code 2021 adventofcode.com/2021/day/8 #AdventOfCode
J'avais juste fabriqué un dico r des règles avec tous les successeurs b de chaque clé a dans une liste.
stackoverflow.com/a/57003713


J'avais juste fabriqué un dico r des règles avec tous les successeurs b de chaque clé a dans une liste.
stackoverflow.com/a/57003713
Il y a 49 items, et chacun a 24 successeurs.
Pour chaque couple, l'un unique est successeur de l'autre.
Si on les code par des lettres, et qu'on trie tout, on voit ça :

Il y a 49 items, et chacun a 24 successeurs.
Pour chaque couple, l'un unique est successeur de l'autre.
Si on les code par des lettres, et qu'on trie tout, on voit ça :
Les programmeurs (les profs de maths ?) ont vraiment du souci à se faire.

Les programmeurs (les profs de maths ?) ont vraiment du souci à se faire.


