🌐 bennywee.github.io
bsky.app/profile/benn...
Source: www.facebook.com/webcomicname...
bsky.app/profile/benn...
2. Is fine but less problem solving ➡️ weaker learning outcomes
I think I learn best with 2. when engaging and talking with other people. So I just have a discord server now where I summarise textbook chapters for ad-hoc discussion
2. Is fine but less problem solving ➡️ weaker learning outcomes
I think I learn best with 2. when engaging and talking with other people. So I just have a discord server now where I summarise textbook chapters for ad-hoc discussion
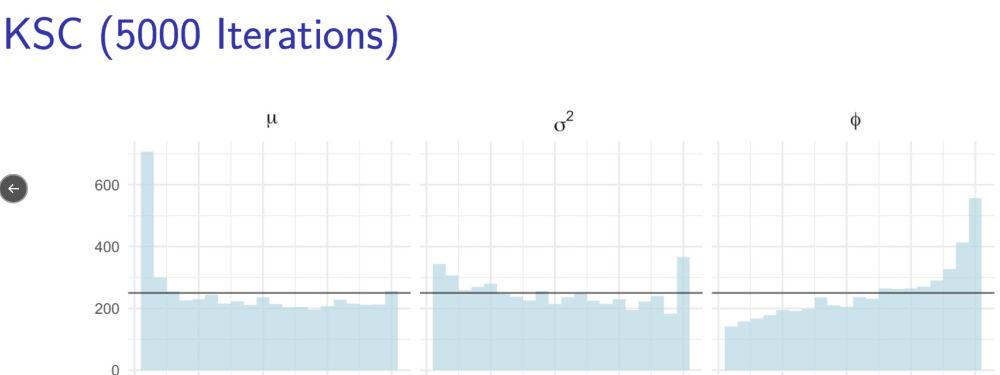
Talts et al (2020): arxiv.org/abs/1804.06788
Kim et al (1998): apps.olin.wustl.edu/faculty/chib...
/end 🧵

Talts et al (2020): arxiv.org/abs/1804.06788
Kim et al (1998): apps.olin.wustl.edu/faculty/chib...
/end 🧵