
https://www.blakecourter.com/
Anyhow, the story seemed like it might be good radio.
Anyhow, the story seemed like it might be good radio.

There are other results based on gradients and intersection curves as well. I was just OCD for rolling ball blends.
There are other results based on gradients and intersection curves as well. I was just OCD for rolling ball blends.
Curious to see if you’re using explicit or implicit geometry and what kind of IDs or classifiers you throw on topology. Also parameterizations.
(At GCL, we make an implicit modeling kernel and work with CAE startups.)
Curious to see if you’re using explicit or implicit geometry and what kind of IDs or classifiers you throw on topology. Also parameterizations.
(At GCL, we make an implicit modeling kernel and work with CAE startups.)
I think I have been capitalizing titles wrong in my bibtex.
I think I have been capitalizing titles wrong in my bibtex.
In the next session, we'll look at that two-surface coordinate system more closely, treating it as a basis for remapping any kind of edge treatment!
(10/n, n = 10)
In the next session, we'll look at that two-surface coordinate system more closely, treating it as a basis for remapping any kind of edge treatment!
(10/n, n = 10)
Algebraic geometers call this family a "pencil".
With such an angled face at any angle and offset, we can describe any surface from the edge in "Hesse normal form".
(9/n)
Algebraic geometers call this family a "pencil".
With such an angled face at any angle and offset, we can describe any surface from the edge in "Hesse normal form".
(9/n)
A * t + B * (1 - t)
Indeed, such interpolating will create suitable geometry, but how do we control it with CAD-like parameters?
(8/n)
A * t + B * (1 - t)
Indeed, such interpolating will create suitable geometry, but how do we control it with CAD-like parameters?
(8/n)
(7/n)
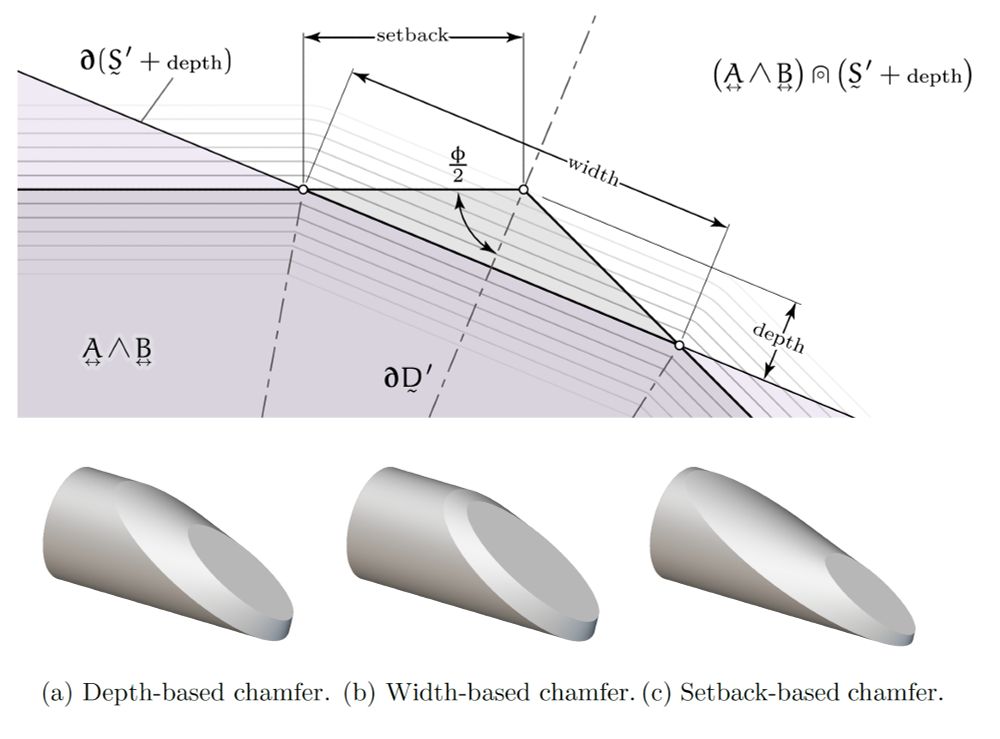
(7/n)
(6/n)

(6/n)
(It's a bit subtle.)
(5/n)
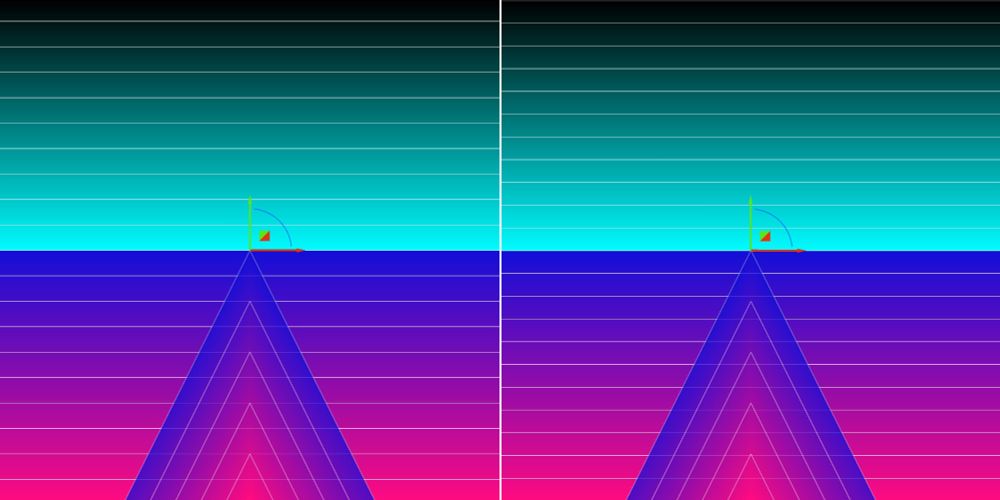
(It's a bit subtle.)
(5/n)
Defining:
S = A + B
D = A - B
Interactive version: www.shadertoy.com/view/dd2cWy
(4/n)
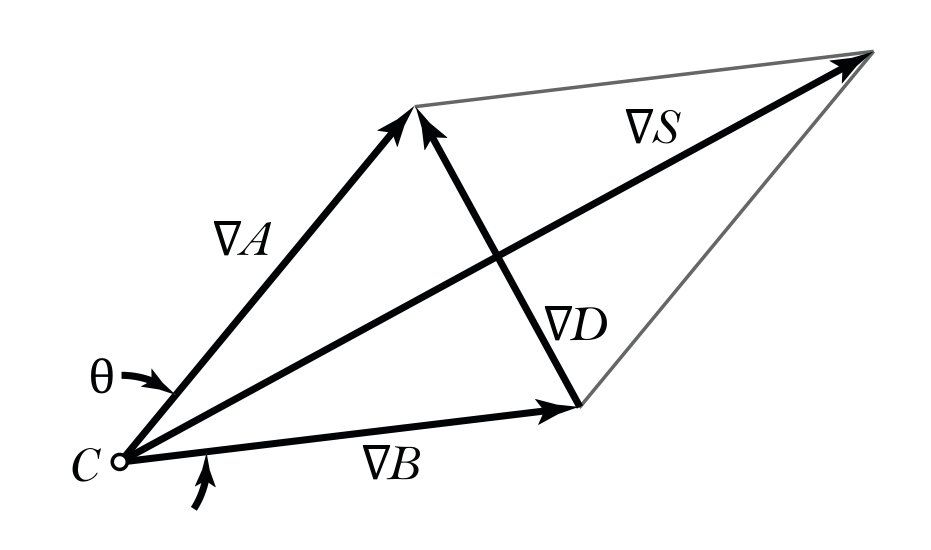
Defining:
S = A + B
D = A - B
Interactive version: www.shadertoy.com/view/dd2cWy
(4/n)

