
https://www.blakecourter.com/
Algebraic geometers call this family a "pencil".
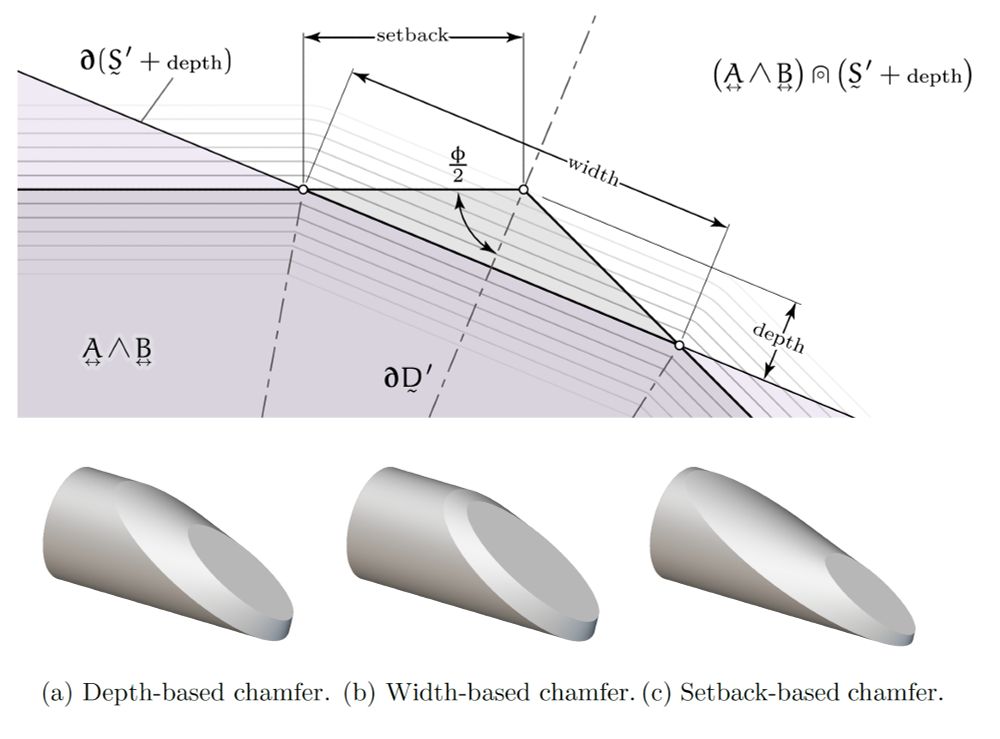
With such an angled face at any angle and offset, we can describe any surface from the edge in "Hesse normal form".
(9/n)
Algebraic geometers call this family a "pencil".
With such an angled face at any angle and offset, we can describe any surface from the edge in "Hesse normal form".
(9/n)
(7/n)
(7/n)
(6/n)

(6/n)
(It's a bit subtle.)
(5/n)
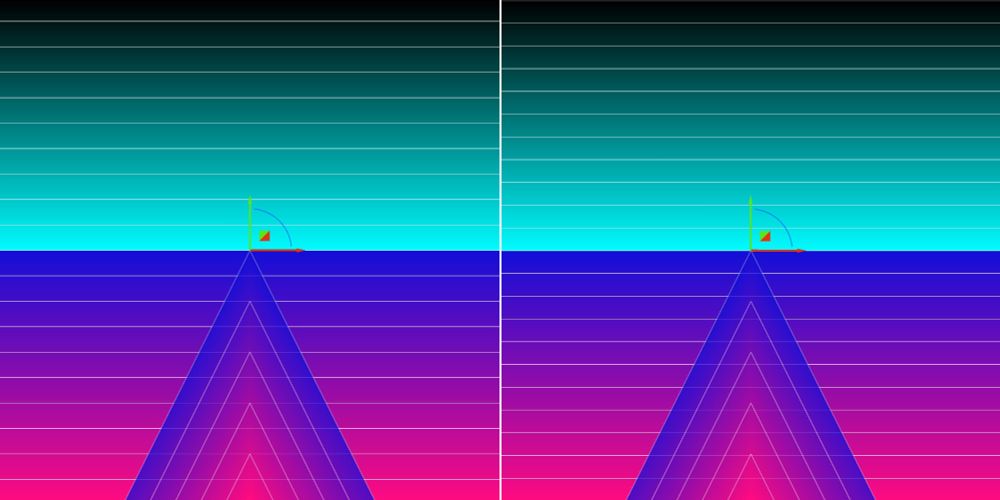
(It's a bit subtle.)
(5/n)
Defining:
S = A + B
D = A - B
Interactive version: www.shadertoy.com/view/dd2cWy
(4/n)
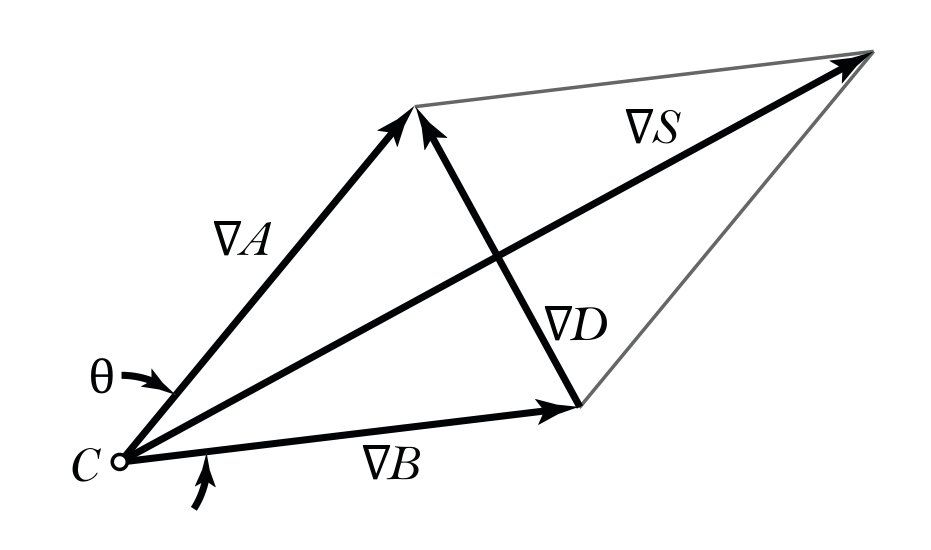
Defining:
S = A + B
D = A - B
Interactive version: www.shadertoy.com/view/dd2cWy
(4/n)
This corner, A ∩ B, is what we want to chamfer. Note that this result is not an SDF, but a UGF, because the field extending up from the corner is sharp.
(3/n)
This corner, A ∩ B, is what we want to chamfer. Note that this result is not an SDF, but a UGF, because the field extending up from the corner is sharp.
(3/n)
Here's A. B will just be it's mirror image across the vertical axis:
(2/n)

Here's A. B will just be it's mirror image across the vertical axis:
(2/n)
(UGFs are a generalization of SDFs considering fields with unit gradient magnitude. www.blakecourter.com/2023/05/18/f...)
Images are from #nTop .
(1/n)

(UGFs are a generalization of SDFs considering fields with unit gradient magnitude. www.blakecourter.com/2023/05/18/f...)
Images are from #nTop .
(1/n)
(6/n)

(6/n)
While interesting, I have not found this aspect of the approach useful for conformally mapping lattices.
(5/n)

While interesting, I have not found this aspect of the approach useful for conformally mapping lattices.
(5/n)
From the blog post here: www.blakecourter.com/2023/07/01/t...
(4/n)

From the blog post here: www.blakecourter.com/2023/07/01/t...
(4/n)
Midsurfacing can be a tricky operation on explicit geometry like meshes and is near unheard of on B-reps.
(3/n)

Midsurfacing can be a tricky operation on explicit geometry like meshes and is near unheard of on B-reps.
(3/n)
Interactive ShaderToy here: www.shadertoy.com/view/DssczX
(2/n)

Interactive ShaderToy here: www.shadertoy.com/view/DssczX
(2/n)
It creates a field that linearly interpolates from -1 at A to +1 at B.
(1/n)

It creates a field that linearly interpolates from -1 at A to +1 at B.
(1/n)
www.blakecourter.com/2023/05/05/w...
www.blakecourter.com/2023/05/18/f...
There's also a big crazy diagram and the beginning of an API for high-level implicit modeling.
Next time: another UGF application.
(5/n) n = 5.

www.blakecourter.com/2023/05/05/w...
www.blakecourter.com/2023/05/18/f...
There's also a big crazy diagram and the beginning of an API for high-level implicit modeling.
Next time: another UGF application.
(5/n) n = 5.
(3/n)

(3/n)
SDFs always refer to a set, but UGFs need not have any boundary or inside components. UGFs facilitate intermediate operations.
(2/n)

SDFs always refer to a set, but UGFs need not have any boundary or inside components. UGFs facilitate intermediate operations.
(2/n)
Common operations on SDFs like offset and booleans fail to result in SDFs. These operations, with care, do result in UGFs!
(1/n)

Common operations on SDFs like offset and booleans fail to result in SDFs. These operations, with care, do result in UGFs!
(1/n)
This process works as long as you keep your boolean results SDF-like, but you don't have to normalize the medial distance field, as it isn't used in the running computation.
(9/n)

This process works as long as you keep your boolean results SDF-like, but you don't have to normalize the medial distance field, as it isn't used in the running computation.
(9/n)
For the union, there are no new internal medial axes, so it's just like the step for M_Old before.
To track the cut loci (medial axis of the set complement), just invert and swap operations.
So with ever boolean, you can keep track of both sets of discontinuities!
(8/n)

For the union, there are no new internal medial axes, so it's just like the step for M_Old before.
To track the cut loci (medial axis of the set complement), just invert and swap operations.
So with ever boolean, you can keep track of both sets of discontinuities!
(8/n)
(7/n)

(7/n)
To combine them, M_A∩B = |M_Old| > |M_New| ? M_Old : M_New. (Remember, it is only correct inside the shape.)
(6/n)

To combine them, M_A∩B = |M_Old| > |M_New| ? M_Old : M_New. (Remember, it is only correct inside the shape.)
(6/n)
(5/n)

(5/n)
We get MA when A wins and MB when B wins. So let's call M_Old = A > B ? MA : MB ....
(4/n)

We get MA when A wins and MB when B wins. So let's call M_Old = A > B ? MA : MB ....
(4/n)
(2/n)

(2/n)

