
https://almostsuremath.com
Also on YouTube: https://www.youtube.com/@almostsure
Will be on connections between Riemann zeta and Brownian motion.
ETA a few days to a week.

Will be on connections between Riemann zeta and Brownian motion.
ETA a few days to a week.

If you were so stupid to do that, then 𝙮𝙤𝙪 𝙬𝙤𝙪𝙡𝙙 𝙣𝙤𝙩 𝙚𝙫𝙚𝙣 𝙗𝙚 𝙖𝙗𝙡𝙚 𝙩𝙤 𝙖𝙙𝙙 𝙧𝙖𝙣𝙙𝙤𝙢 𝙫𝙖𝙧𝙞𝙖𝙗𝙡𝙚𝙨 𝙩𝙤𝙜𝙚𝙩𝙝𝙚𝙧.



If you were so stupid to do that, then 𝙮𝙤𝙪 𝙬𝙤𝙪𝙡𝙙 𝙣𝙤𝙩 𝙚𝙫𝙚𝙣 𝙗𝙚 𝙖𝙗𝙡𝙚 𝙩𝙤 𝙖𝙙𝙙 𝙧𝙖𝙣𝙙𝙤𝙢 𝙫𝙖𝙧𝙞𝙖𝙗𝙡𝙚𝙨 𝙩𝙤𝙜𝙚𝙩𝙝𝙚𝙧.


And, gamma(1) process scaled to hit 1 at time 1 (time parameter mu to compare). Corresponds to t=0.5 in the surface plot. You can see its dominated by a few large jumps.
gamma(40) process is shown in the 3rd plot, corresponds with t=0.024

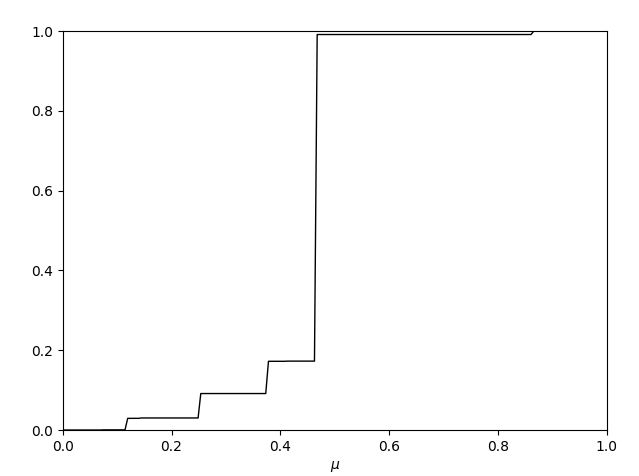

And, gamma(1) process scaled to hit 1 at time 1 (time parameter mu to compare). Corresponds to t=0.5 in the surface plot. You can see its dominated by a few large jumps.
gamma(40) process is shown in the 3rd plot, corresponds with t=0.024
X(μ,t) ~ Beta(μ(1-t)/t, (1-μ)(1-t)/t)
The (1-t)/t scaling is so that on range 0<t<1 we cover entire set of Beta distributions.
For each t, X(μ_{i+1},t)-X(μ_i,t) have Dirichlet distribution.


X(μ,t) ~ Beta(μ(1-t)/t, (1-μ)(1-t)/t)
The (1-t)/t scaling is so that on range 0<t<1 we cover entire set of Beta distributions.
For each t, X(μ_{i+1},t)-X(μ_i,t) have Dirichlet distribution.
If X,Y are independent Gamma(a), Gamma(b) random variables then
X/(X+Y), X+Y
are independent Beta(a,b), Gamma(a+b) rvs.
Equivalently: if X,Y are independent Beta(a,b), Gamma(a+b) random variables then
XY, (1-X)Y
are independent Gamma(a), Gamma(b) rvs.

If X,Y are independent Gamma(a), Gamma(b) random variables then
X/(X+Y), X+Y
are independent Beta(a,b), Gamma(a+b) rvs.
Equivalently: if X,Y are independent Beta(a,b), Gamma(a+b) random variables then
XY, (1-X)Y
are independent Gamma(a), Gamma(b) rvs.
If c = (pa+qb)/(p+q) for p,q > 0 then
f(c)≤M(t)≤(pf(a)+qf(b))/(p+q)
where M(t) is the average value of f under Beta(qt,pt) distribution scaled to interval [a,b].
M(t) is ctsly decreasing from
M(0)=(pf(a)+qf(b))/(p+q)
to
M(∞) = f(c)
pbs.twimg.com/media/GoSUpd...

If c = (pa+qb)/(p+q) for p,q > 0 then
f(c)≤M(t)≤(pf(a)+qf(b))/(p+q)
where M(t) is the average value of f under Beta(qt,pt) distribution scaled to interval [a,b].
M(t) is ctsly decreasing from
M(0)=(pf(a)+qf(b))/(p+q)
to
M(∞) = f(c)
pbs.twimg.com/media/GoSUpd...
Equivalent to existence of a reverse-time martingale X_t ~ Beta(at,bt).
Equivalently:
-(d/dt)E[(x-X_t)_+] >=0
for all 0 < x < 1.
Plots suggest so: parameterised as s=a+b,mean=a/s

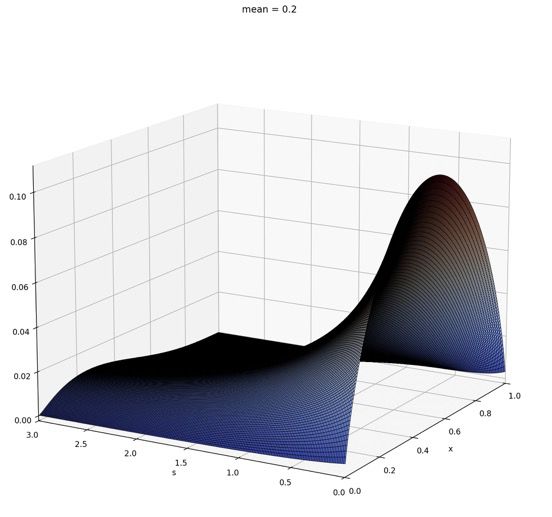


Equivalent to existence of a reverse-time martingale X_t ~ Beta(at,bt).
Equivalently:
-(d/dt)E[(x-X_t)_+] >=0
for all 0 < x < 1.
Plots suggest so: parameterised as s=a+b,mean=a/s


That’s what Wikipedia, and many other sources say. But, no!
Looking up the original source, he's actually being positive about Weierstrass' work!



That’s what Wikipedia, and many other sources say. But, no!
Looking up the original source, he's actually being positive about Weierstrass' work!

Continuous, nowhere differentiable, unbounded variation, no intervals of increase or decrease. Fractal dimension 3/2.
All things it has in common with mathematical Brownian motion
Continuous, nowhere differentiable, unbounded variation, no intervals of increase or decrease. Fractal dimension 3/2.
All things it has in common with mathematical Brownian motion

"Measuring the Earth...from a vacation photo!"
(correct link this time: youtu.be/038AkmPvltA)

"Measuring the Earth...from a vacation photo!"
(correct link this time: youtu.be/038AkmPvltA)

Island is visible, checking Google maps it’s Nevis Island.
Looks like it slopes steeply into the sea, but pics show a lot of flatter land.
Why? Lower bits are over horizon, due to Earth’s curvature!




Island is visible, checking Google maps it’s Nevis Island.
Looks like it slopes steeply into the sea, but pics show a lot of flatter land.
Why? Lower bits are over horizon, due to Earth’s curvature!


