


Is there an analogous construction for term-level fixpoints?
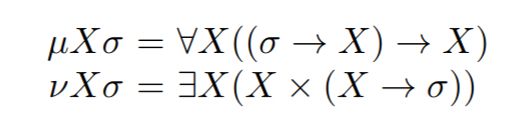
Is there an analogous construction for term-level fixpoints?
I'm trying to implement a calculus that's based on linear proof nets, but they use contextual semantics in a cruicial way, and I just can't get my head around it

I'm trying to implement a calculus that's based on linear proof nets, but they use contextual semantics in a cruicial way, and I just can't get my head around it

We can use polarity and chirality (duality between producers and consumers) to develop a canonical bidirectional typing discipline that requires minimal annotations.
msp.cis.strath.ac.uk/msp101.html

We can use polarity and chirality (duality between producers and consumers) to develop a canonical bidirectional typing discipline that requires minimal annotations.
msp.cis.strath.ac.uk/msp101.html


once your language supports disjunctive outputs, the output of an if-then-else statement no longer needs to be monotyped - it's type can depend on the branch taken

once your language supports disjunctive outputs, the output of an if-then-else statement no longer needs to be monotyped - it's type can depend on the branch taken
So this program takes a sum (s : Either a b) and branches off into two branches, one of which outputs (this : a) and the other (that : b)

So this program takes a sum (s : Either a b) and branches off into two branches, one of which outputs (this : a) and the other (that : b)

This is why - Dependent types are letting us develop next-generation compiler tech:

This is why - Dependent types are letting us develop next-generation compiler tech:
do you want another language for writing a login form or reversing a linked list,
or do you want a PL that lets you break into the platonic realm so you can pillage it for abstractions

do you want another language for writing a login form or reversing a linked list,
or do you want a PL that lets you break into the platonic realm so you can pillage it for abstractions
Sums are dual to products, tensor is dual to par.

Sums are dual to products, tensor is dual to par.

all I had to do was to come up with a new bidirectional typing algorithm to get rid of all the type annotations

all I had to do was to come up with a new bidirectional typing algorithm to get rid of all the type annotations









