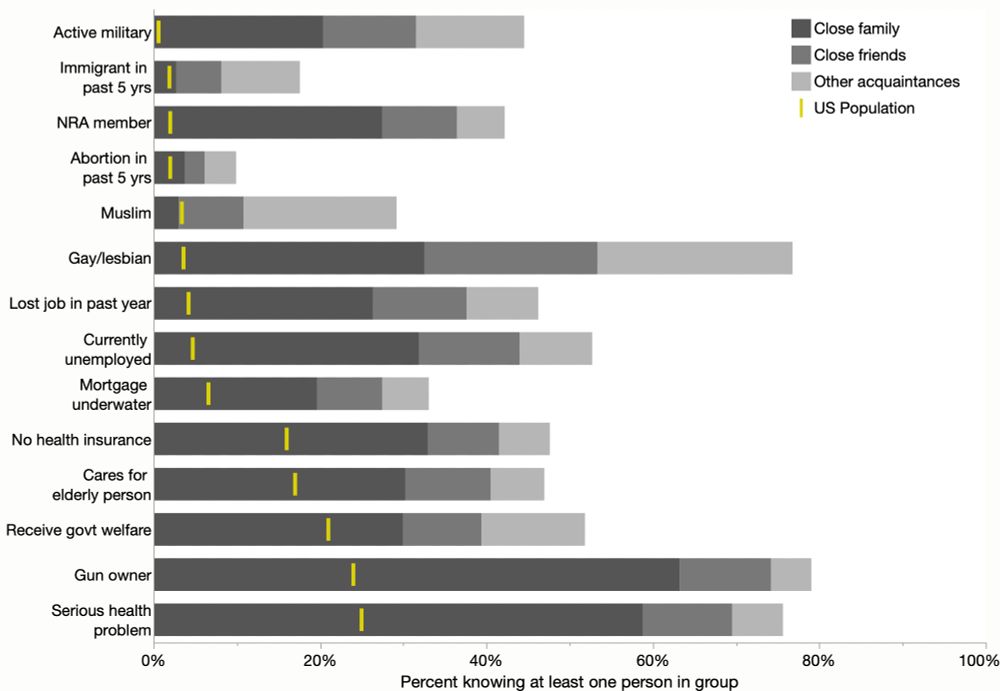
observablehq.com/@xangregg/lo...

observablehq.com/@xangregg/lo...
rawdatastudies.com/2025/10/26/n...


rawdatastudies.com/2025/10/26/n...
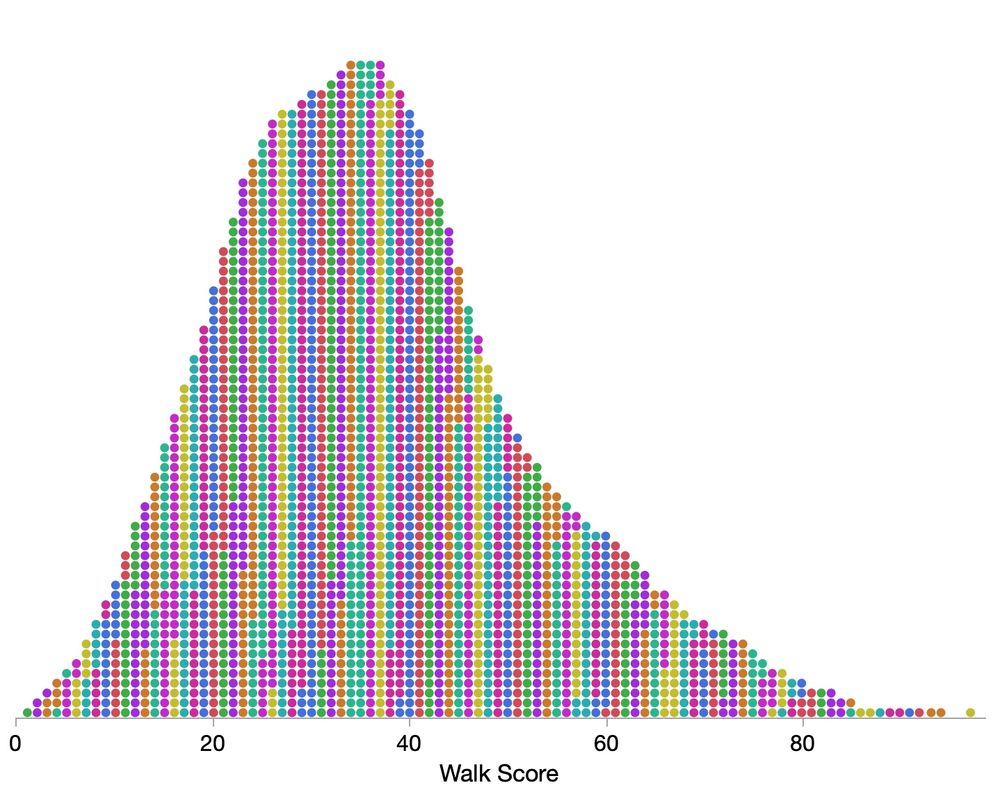
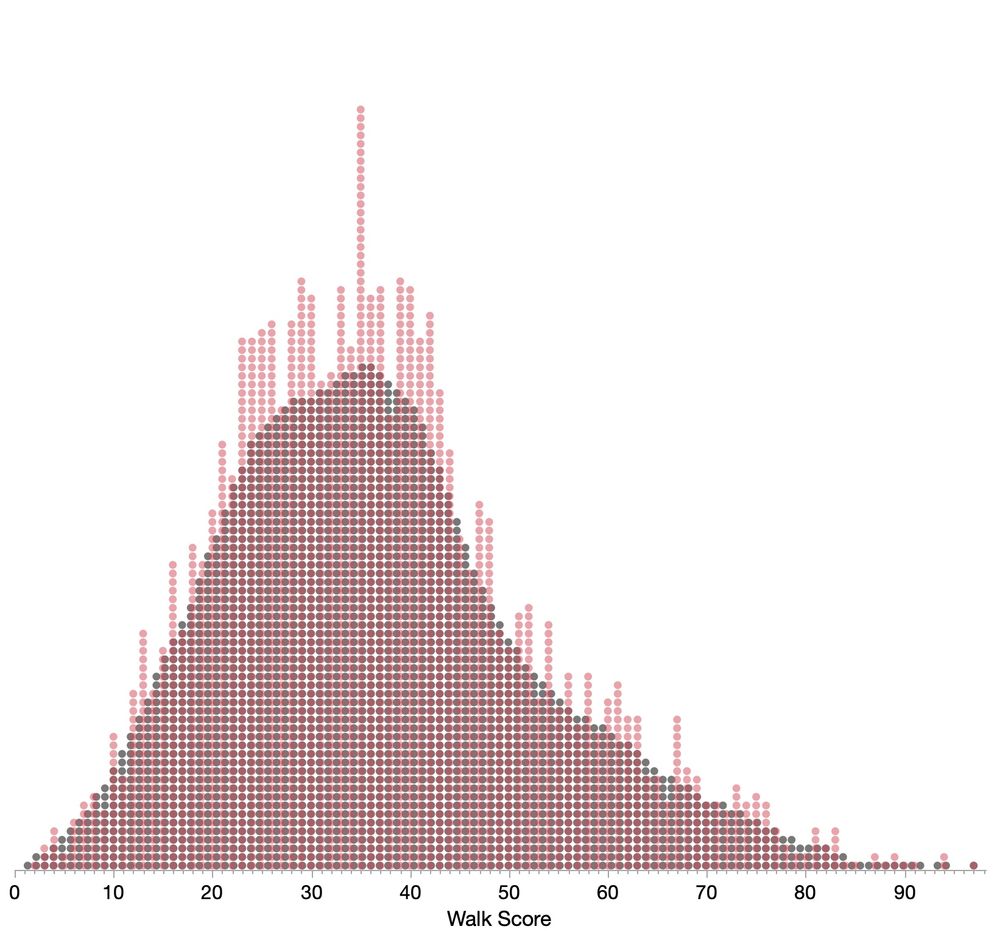
1 Nearest stacks (Wilkinson)
2 Smoothed stacks
3 Smoothed hexagonal grid
4 Exact position (beeswarm)
Smoothing trades delta-x for spikiness (deviation from kernel density estimate).




1 Nearest stacks (Wilkinson)
2 Smoothed stacks
3 Smoothed hexagonal grid
4 Exact position (beeswarm)
Smoothing trades delta-x for spikiness (deviation from kernel density estimate).
community.jmp.com/t5/JMPer-Cab...

community.jmp.com/t5/JMPer-Cab...




Curiously, these line charts are random data, suggesting steadier step counts. www.nature.com/articles/s41...

![Screenshot from a Python notebook shared with the paper. Code part reads:
with plt.rc_context({'figure.autolayout': True}):
fig, ax = plt.subplots(figsize=(4, 2));
pre_x = range(-35, -5);
y = np.random.normal(loc=from_df.loc[from_df['from_loc'] == 'Seattle, WA', 'pre_avg'], scale=50., size=(len(pre_x), ));
plt.plot(pre_x, y, lw=5., c='#aa3939');
plt.ylim(5800, 7000);
ax.grid(False);
for item in ([ax.xaxis.label, ax.yaxis.label] + ax.get_xticklabels() + ax.get_yticklabels()):
item.set_fontsize(axis_fontsize);
ax.set(xlabel=r'Days from Move $\left(t - t_{move}\right)$', ylabel='Daily Steps', xticks=range(-35, -4, 10));
fig.tight_layout()
plt.savefig('../output/fig1b_subplots/seattle_from.png',
dpi=600);](https://cdn.bsky.app/img/feed_thumbnail/plain/did:plc:vum7yuqczgryxehx6ozitxjg/bafkreifl6rfkiphf3g3ryzskgo4vg6vj2pw7wcwhh4e3jr6rxf52434bqy@jpeg)
Curiously, these line charts are random data, suggesting steadier step counts. www.nature.com/articles/s41...




arxiv.org/pdf/2402.14583

arxiv.org/pdf/2402.14583


He's a control charts expert, which explains the sequence-based context and small data sizes.

He's a control charts expert, which explains the sequence-based context and small data sizes.

I realized my adaptive outlier idea was already done as Grubbs' test, which I've adapted for non-gaussian moments.
Added a couple thirds-based views. Here's 5000 random normal samples plus 2 outliers. The green ones use Grubbs.

I realized my adaptive outlier idea was already done as Grubbs' test, which I've adapted for non-gaussian moments.
Added a couple thirds-based views. Here's 5000 random normal samples plus 2 outliers. The green ones use Grubbs.
1) many false outliers for big data
2) no outliers for small data
3) regions can extend beyond the data
Still tuning, but the code is in JavaScript at github.com/xangregg/dat....

1) many false outliers for big data
2) no outliers for small data
3) regions can extend beyond the data
Still tuning, but the code is in JavaScript at github.com/xangregg/dat....
Old Faithful eruption intervals bimodal data,
Random bimodal
Random exponential
Random lognormal




Old Faithful eruption intervals bimodal data,
Random bimodal
Random exponential
Random lognormal