All this is with little to no fine-tuning! Simply initialising hidden layers with a small variance allows our model to use additional layers just when necessary, preventing overfitting in our experiments.

See our paper here: arxiv.org/abs/2411.00161. 9/n

Lastly, we demonstrate that residual deep GPs can be faster than Euclidean deep GPs, by projecting Euclidean data to a compact manifold. 8/n

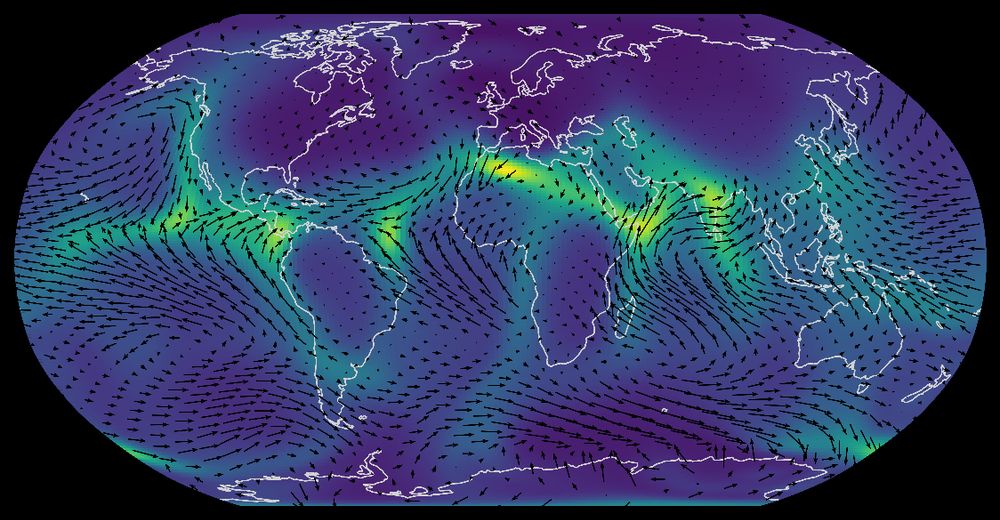
We test our model on the ERA5 dataset – interpolating wind on the globe from a set of points on a satellite trajectory. Our model outperforms baselines, yielding accurate and interpretable uncertainty estimates. An example predictive mean and variance is shown below. 7/n

Our model can also serve as a plug-and-play replacement for shallow manifold GPs in geometry-aware Bayesian optimisation. This can be especially useful for complex target functions, as we demonstrate experimentally. 6/n

With manifold GPs at every layer, we can leverage manifold-specific methods like intrinsic Gaussian vector fields and interdomain inducing variables to improve performance. 5/n

We can build deep GPs by stacking these layers. Each layer learns a translation of inputs, allowing incremental updates of hidden representations – just like the ResNet! In fact, on the Euclidean manifold, we recover the ResNet-inspired deep GP of Salimbeni & @deisenroth.bsky.social. 4/n

Not quite. On general manifolds, points and tangent vectors cannot be identified. We can, however, translate points in the direction of vectors using the exponential map. Thus, we define a manifold-to-manifold GP as a composition of a Gaussian vector field with this map. 3/n

When Euclidean GPs struggle to model irregular functions, stacking them into a deep GPs can help. This works because points and vectors in Euclidean space can be identified, allowing a vector-valued GP’s output to serve as another’s input. But can we do this on manifolds? 2/n