To figure out what was going on, I made an animation. I found that Anita the Ant's path ended up inscribing a 2-3-2 isosceles triangle.
To figure out what was going on, I made an animation. I found that Anita the Ant's path ended up inscribing a 2-3-2 isosceles triangle.

Here are the average lengths of the longest increasing subsequences of all the permutations of n elements.
(The numerators in the table come from oeis.org/A003316.)

Here are the average lengths of the longest increasing subsequences of all the permutations of n elements.
(The numerators in the table come from oeis.org/A003316.)
This chart shows how the number of mulligans you have affects your expected score.

This chart shows how the number of mulligans you have affects your expected score.
This chart shows the probability of being able to achieve various dollar amounts of cash if you start with three $10 vouchers and one $25 voucher and play optimally for each amount.

This chart shows the probability of being able to achieve various dollar amounts of cash if you start with three $10 vouchers and one $25 voucher and play optimally for each amount.
I wrote code to emulate playing the game of bowling. I found 420,571 possible states in the game including 25,646 terminal states.
With this list in hand, it was a matter of finding the terminal states that best qualified in each case.



I wrote code to emulate playing the game of bowling. I found 420,571 possible states in the game including 25,646 terminal states.
With this list in hand, it was a matter of finding the terminal states that best qualified in each case.
I found 324 different shapes of parallelogram. The smallest appeared at 124 different locations and orientations.

I found 324 different shapes of parallelogram. The smallest appeared at 124 different locations and orientations.
How many different equilateral triangles in the game of Dozo?
I found 11 different sizes of triangle. The smallest appeared at 36 different locations and orientations on the Dozo board. The largest appeared just once.
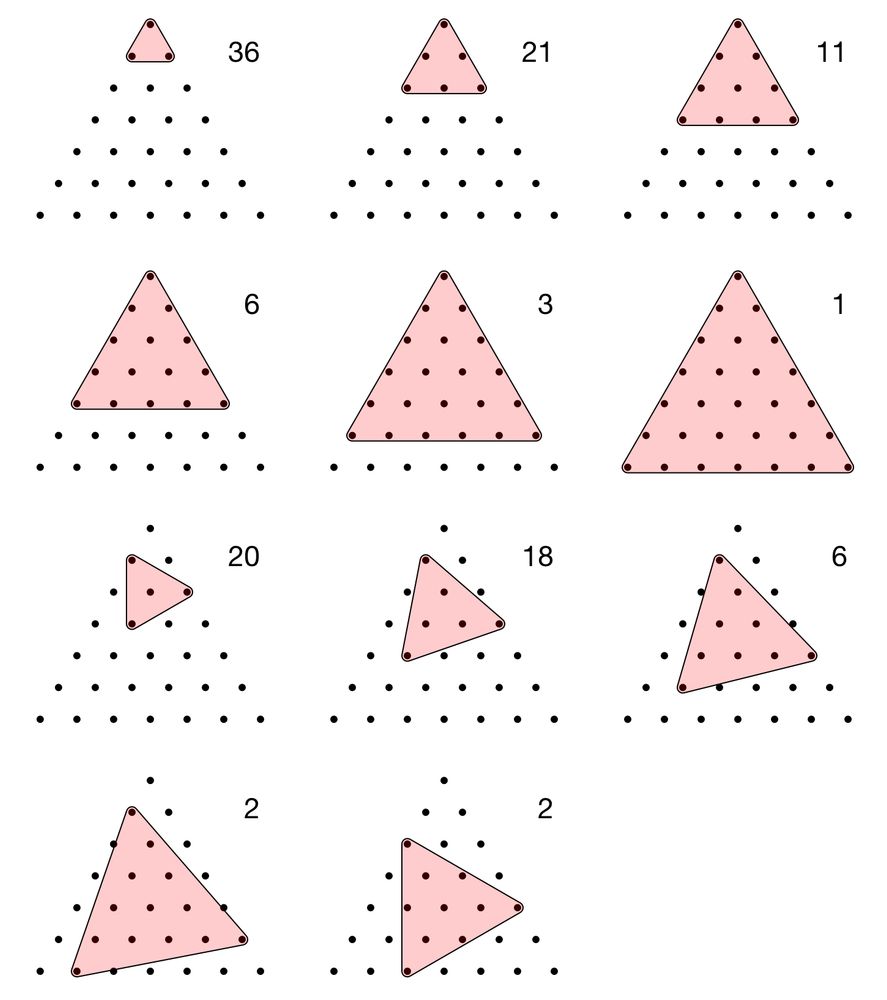
How many different equilateral triangles in the game of Dozo?
I found 11 different sizes of triangle. The smallest appeared at 36 different locations and orientations on the Dozo board. The largest appeared just once.

Here are my first three cuts.
Here are my first three cuts.
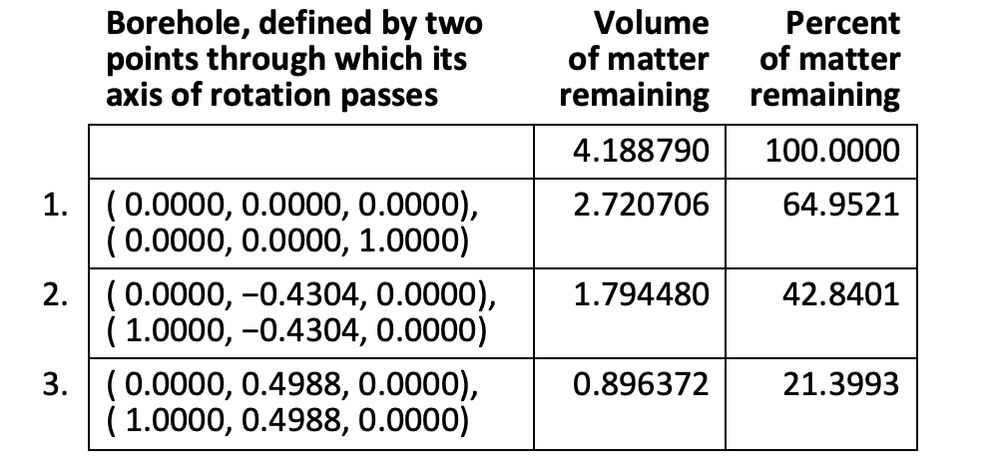
Here is "a" solution to the extra credit. Very likely not "the" solution because I could only approximately calculate the volume remaining and couldn't figure out a way to find the greediest cylinder at each step.
I obliterated the sphere in 12 steps. YMMV.
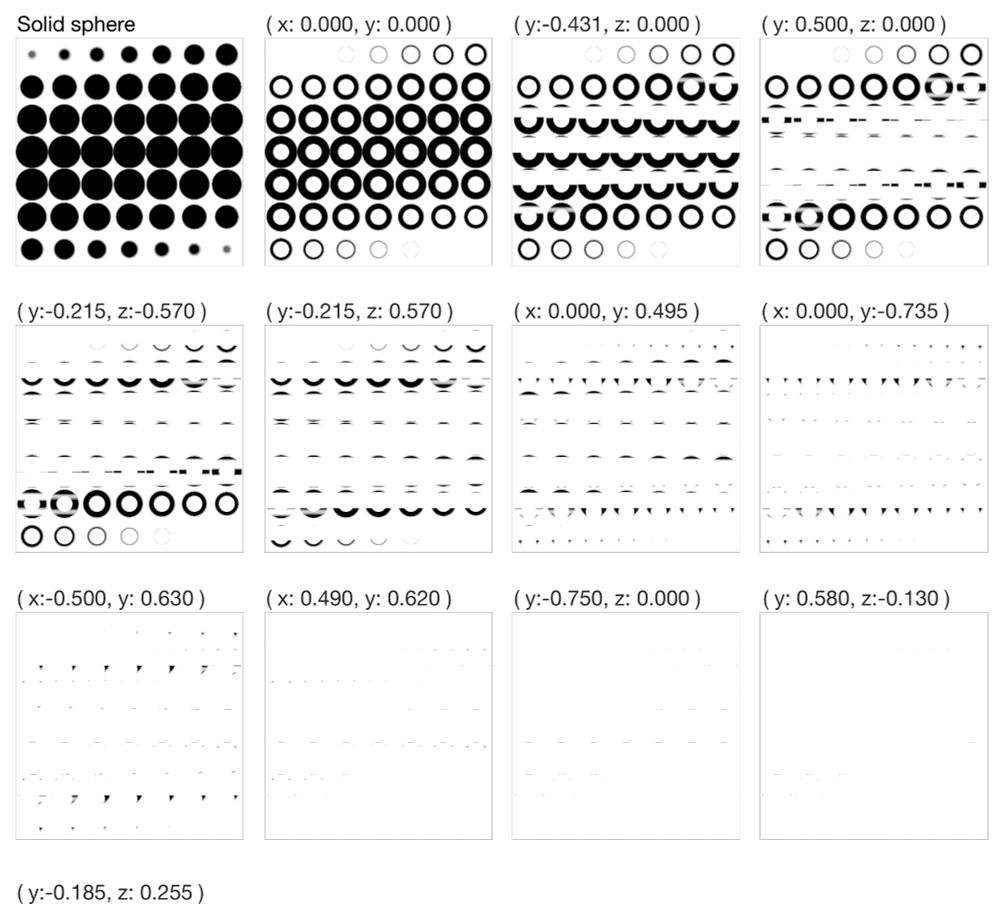
Here is "a" solution to the extra credit. Very likely not "the" solution because I could only approximately calculate the volume remaining and couldn't figure out a way to find the greediest cylinder at each step.
I obliterated the sphere in 12 steps. YMMV.
A 10-long river like this one happens only 405 times out of every 1,073,741,824.

A 10-long river like this one happens only 405 times out of every 1,073,741,824.
Let's count them up ...

Let's count them up ...
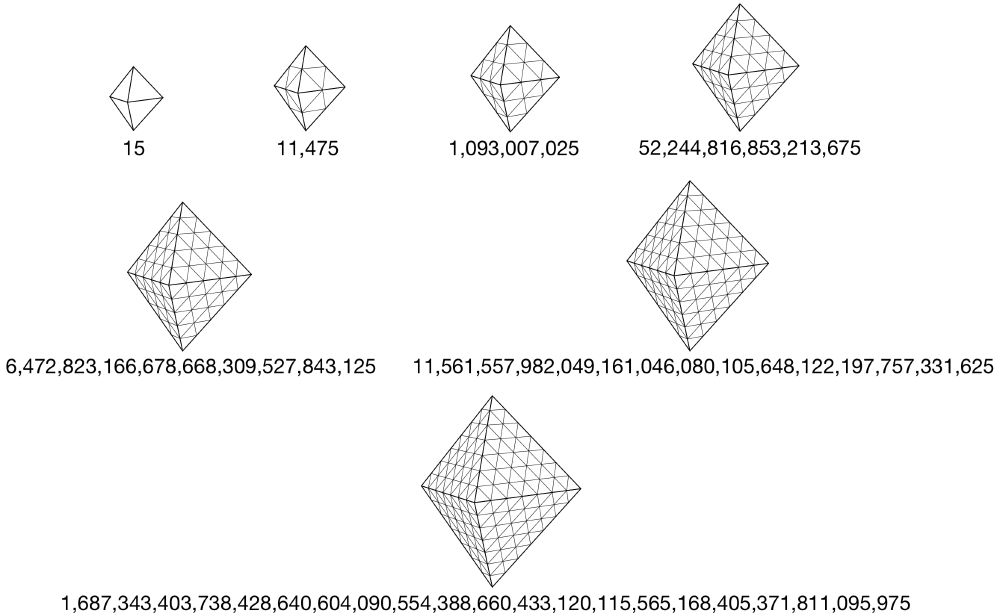
Extra credit: How many distinct paths are there from the top of a triangular bipyramid to the bottom, if (1) you never visit the same point twice and (2) you move only downward or sideways?
Short answer: A lot, especially with larger bipyramids.
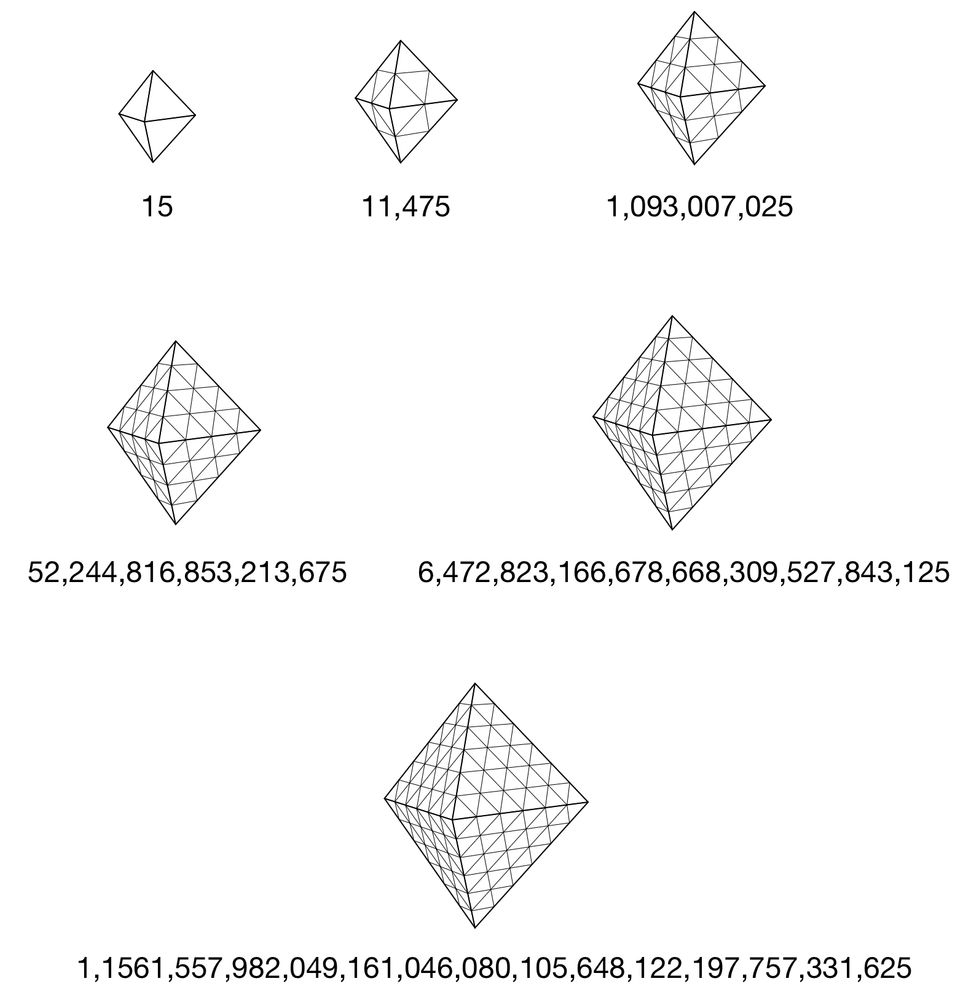
Extra credit: How many distinct paths are there from the top of a triangular bipyramid to the bottom, if (1) you never visit the same point twice and (2) you move only downward or sideways?
Short answer: A lot, especially with larger bipyramids.
Somehow I was expecting something simpler.
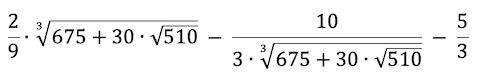
Somehow I was expecting something simpler.
Let c = value of p where p7 = p4.
Then the answer is (b - c) / (b - a).
Let c = value of p where p7 = p4.
Then the answer is (b - c) / (b - a).
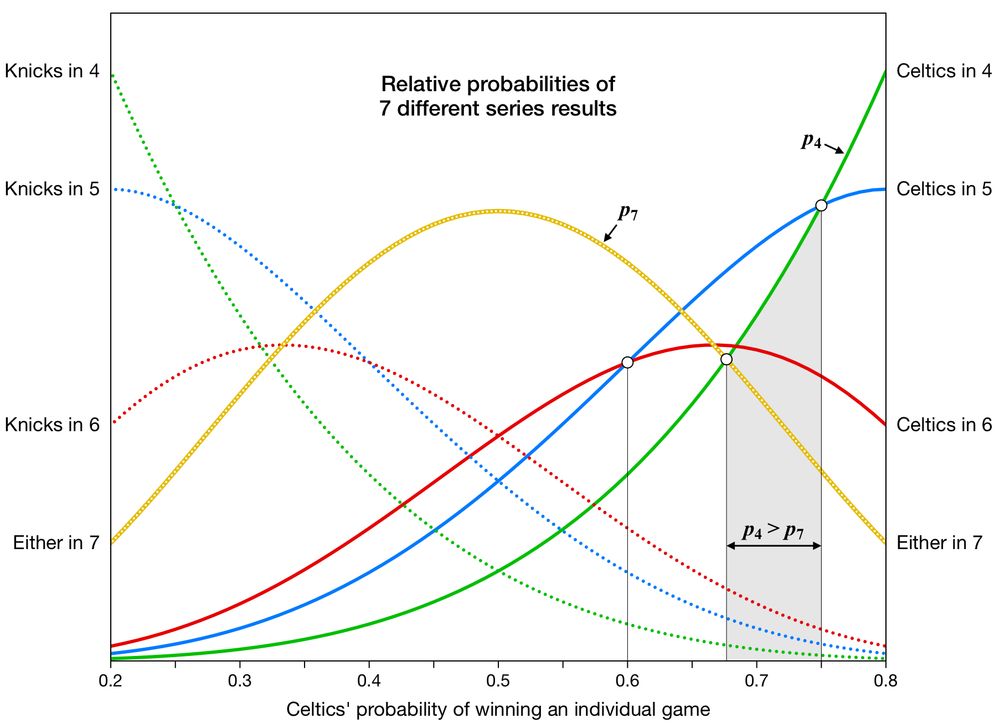
This chart shows how the likelihood of each series result depends on the probability p of the Celtics winning an individual game.
The likelihood of "Celtics in 5" (blue line) is greater than the likelihood of any other result when p is between 0.6 and 0.75.

This chart shows how the likelihood of each series result depends on the probability p of the Celtics winning an individual game.
The likelihood of "Celtics in 5" (blue line) is greater than the likelihood of any other result when p is between 0.6 and 0.75.
Now the relative size of the gaps depends on the exact visibility. (The tree at (8,1)'s gap is larger 60% of the time.) It doesn't settle one way or the other no matter how large your visibility gets.
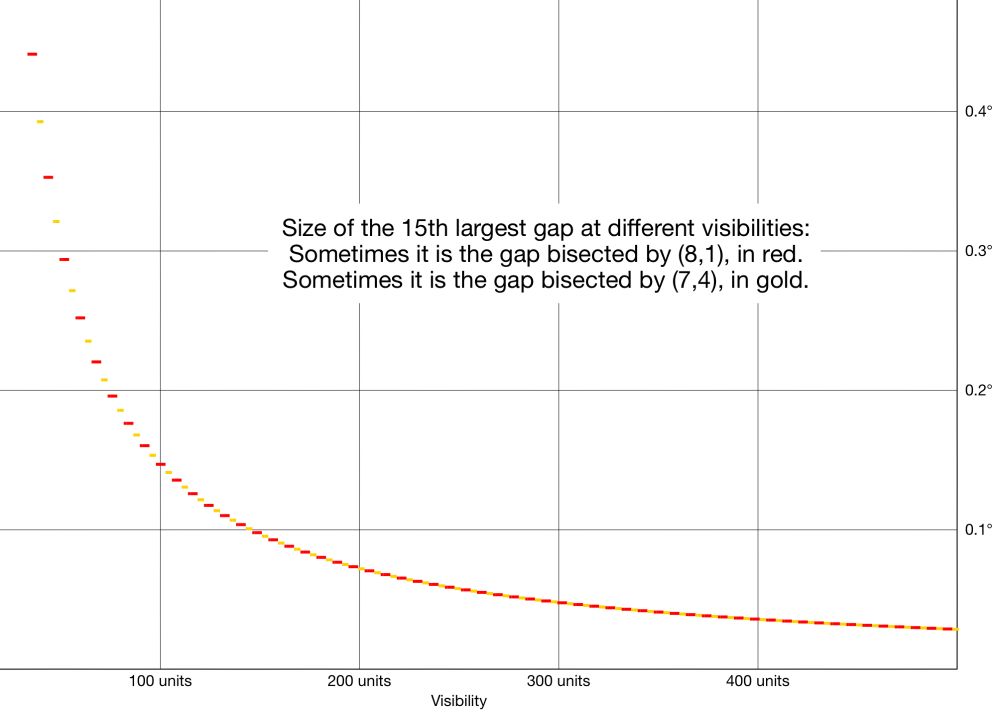
Now the relative size of the gaps depends on the exact visibility. (The tree at (8,1)'s gap is larger 60% of the time.) It doesn't settle one way or the other no matter how large your visibility gets.
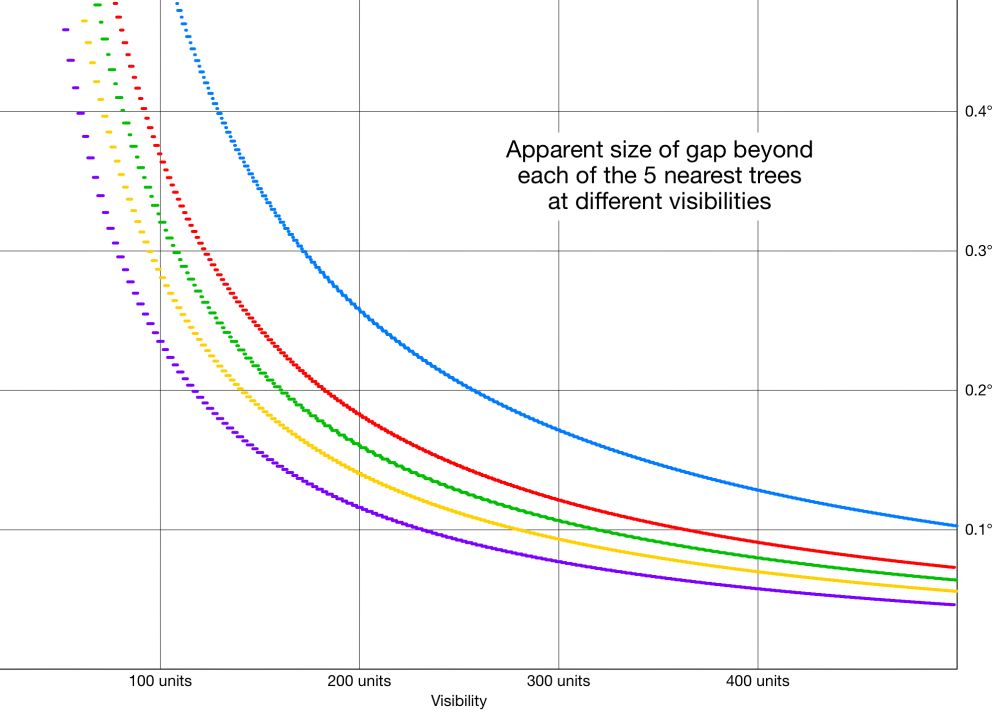
The largest gaps seem to lie on either side of the nearest trees. The nearest tree is at (2,1) and it separates the 2 largest gaps. The next nearest trees are at (3,1), (3,2), (4,1), and (4,3).
The illustration shows gaps when visibility is 100.
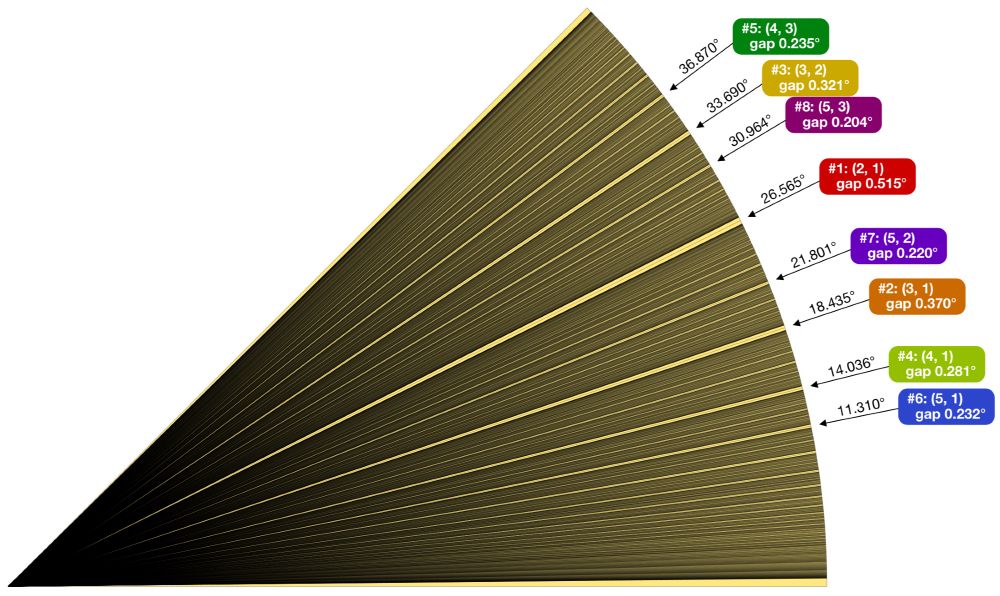
The largest gaps seem to lie on either side of the nearest trees. The nearest tree is at (2,1) and it separates the 2 largest gaps. The next nearest trees are at (3,1), (3,2), (4,1), and (4,3).
The illustration shows gaps when visibility is 100.
There seems to be a pattern for the number of teams that can never win a tournament. If the number of teams in the tournament is 2^k, then the number of teams that can never win is 2^(k-1) - k + 1 (in the general case).
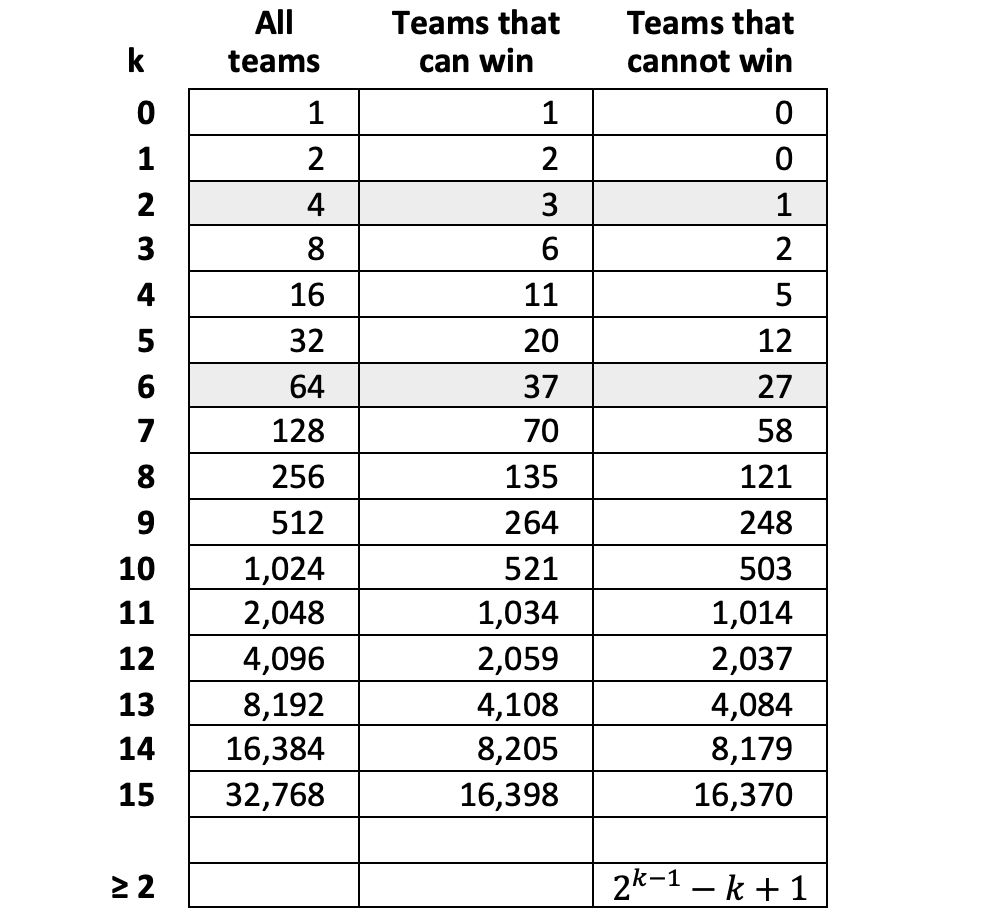
There seems to be a pattern for the number of teams that can never win a tournament. If the number of teams in the tournament is 2^k, then the number of teams that can never win is 2^(k-1) - k + 1 (in the general case).
I tried running the tournament with different boost values, namely 0.5, 1.5, 2.5, and 3.5.
Every team won except for the team with power index 3.

I tried running the tournament with different boost values, namely 0.5, 1.5, 2.5, and 3.5.
Every team won except for the team with power index 3.


