
Working on physics-informed ML and probabilistic numerics at Philipp Hennig's group in Tübingen.
https://timwei.land
Construct a linear stochastic proxy to the PDE you want to solve -> discretize to get a GMRF -> Gauss-Newton + sparse linear algebra to get a posterior which is informed about your data and the PDE. 7/8
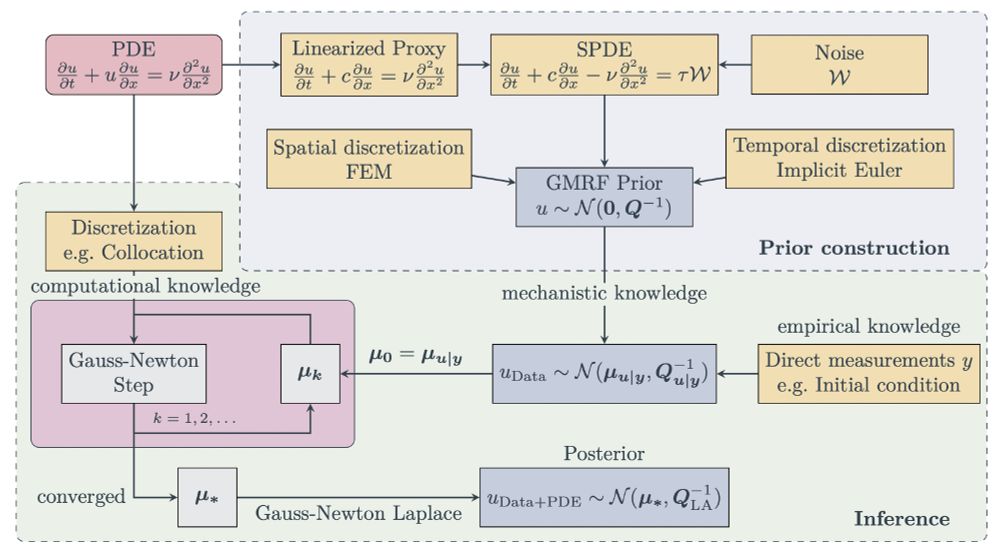
Construct a linear stochastic proxy to the PDE you want to solve -> discretize to get a GMRF -> Gauss-Newton + sparse linear algebra to get a posterior which is informed about your data and the PDE. 7/8
With this approach, we express our prior belief through an SPDE.
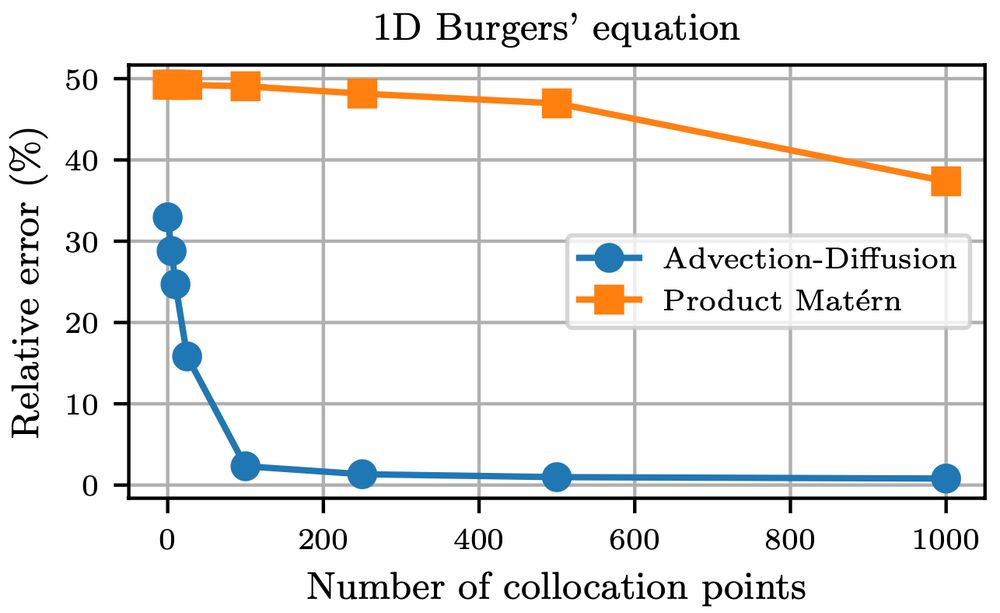
Then why should we use the Whittle-Matérn SPDE?
Instead, why don't we construct a linear SPDE that more closely captures the dynamics we care about? 5/8
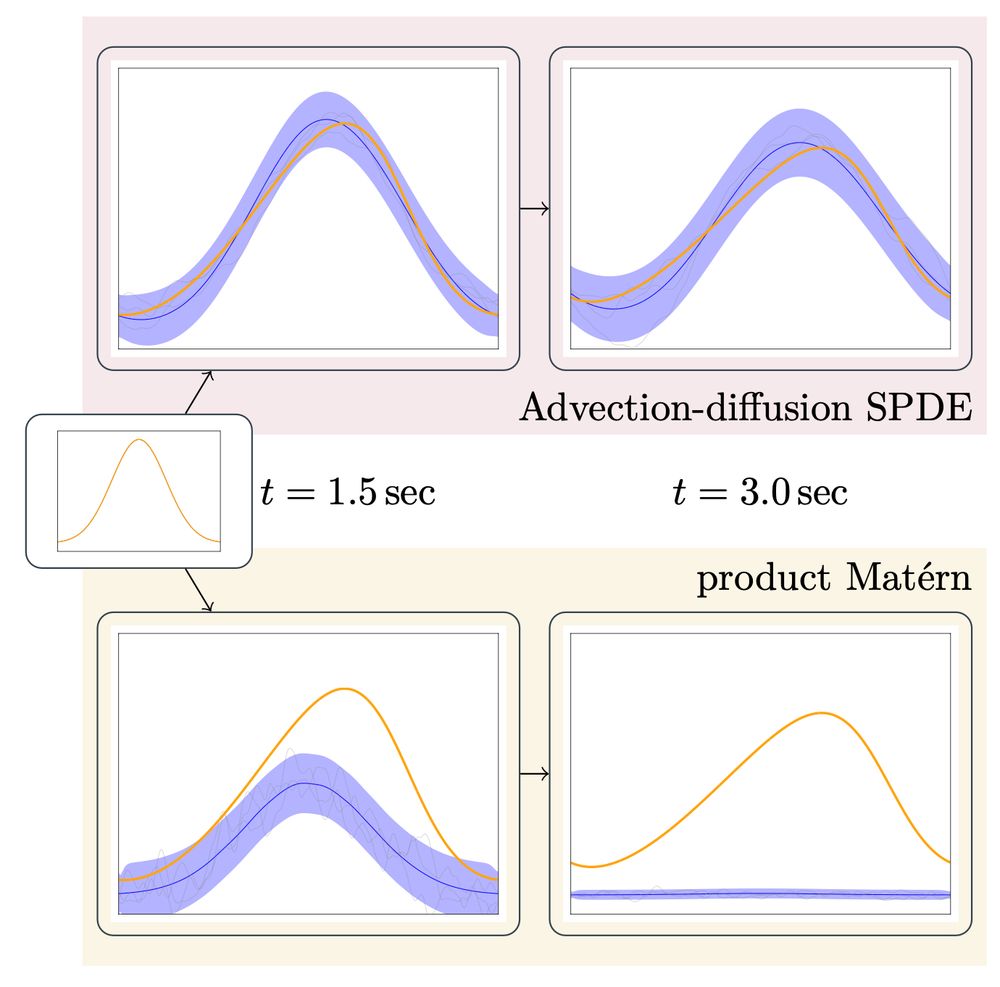
With this approach, we express our prior belief through an SPDE.
Then why should we use the Whittle-Matérn SPDE?
Instead, why don't we construct a linear SPDE that more closely captures the dynamics we care about? 5/8
So we get a FEM representation of the solution function, with stochastic weights given by a GMRF.
Now we just need to "inform" these weights about a discretization of the PDE we want to solve.
These computations are highly efficient, due to the magic of ✨sparse linear algebra✨. 4/8
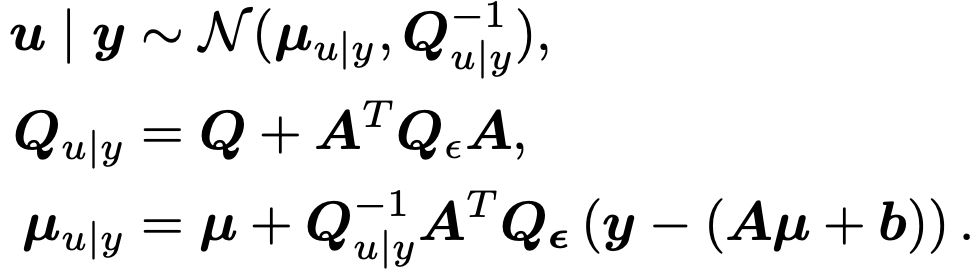
So we get a FEM representation of the solution function, with stochastic weights given by a GMRF.
Now we just need to "inform" these weights about a discretization of the PDE we want to solve.
These computations are highly efficient, due to the magic of ✨sparse linear algebra✨. 4/8
In 2011, Lindgren et al. used the finite element method (FEM) to discretize this SPDE.
This results in a Gaussian Markov Random Field (GMRF), a Gaussian with a sparse precision matrix. 3/8
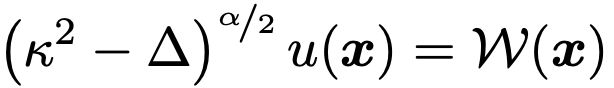
In 2011, Lindgren et al. used the finite element method (FEM) to discretize this SPDE.
This results in a Gaussian Markov Random Field (GMRF), a Gaussian with a sparse precision matrix. 3/8
Read on to learn about the exciting interplay of stochastic PDEs, Markov structures and sparse linear algebra that make it possible... 🧵 1/8
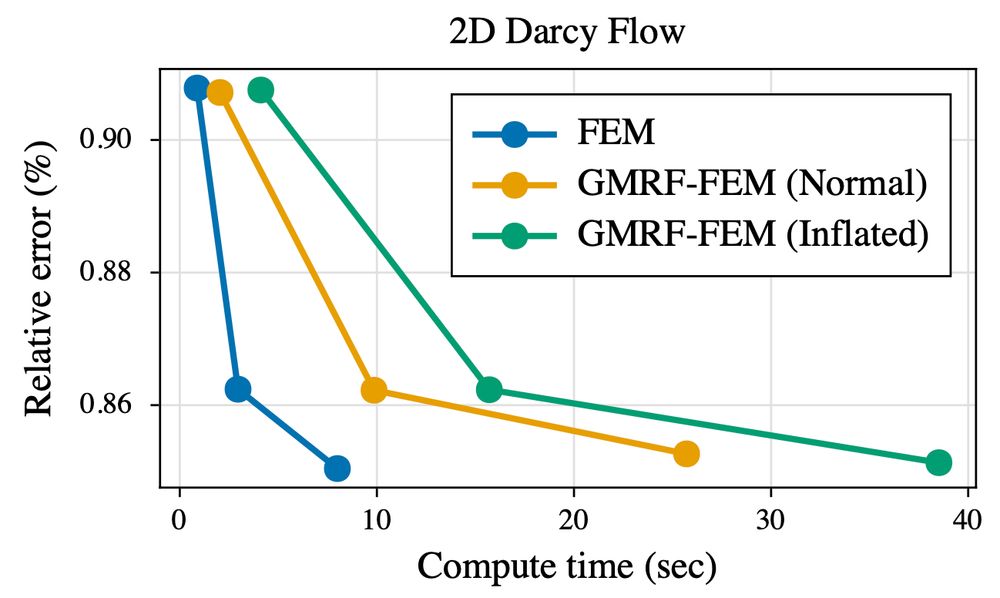
Read on to learn about the exciting interplay of stochastic PDEs, Markov structures and sparse linear algebra that make it possible... 🧵 1/8

