https://tamasgorbe.com/
The integral symbol is 350 years old! On October 29th, 1675 Leibniz has written down the first ever integral sign (see the image).
Let's celebrate integral day by sharing your favourite integral or integral related fact / content.

The integral symbol is 350 years old! On October 29th, 1675 Leibniz has written down the first ever integral sign (see the image).
Let's celebrate integral day by sharing your favourite integral or integral related fact / content.
steel beams, light beams, and water streams
building sways, ocean waves, and sound waves...”
— Peter Lax (1926-2025)
steel beams, light beams, and water streams
building sways, ocean waves, and sound waves...”
— Peter Lax (1926-2025)
Definitions < Theorems
Me (now):
Definitions > Theorems
Definitions < Theorems
Me (now):
Definitions > Theorems

the determinant of the exponential equals the exponential of the trace
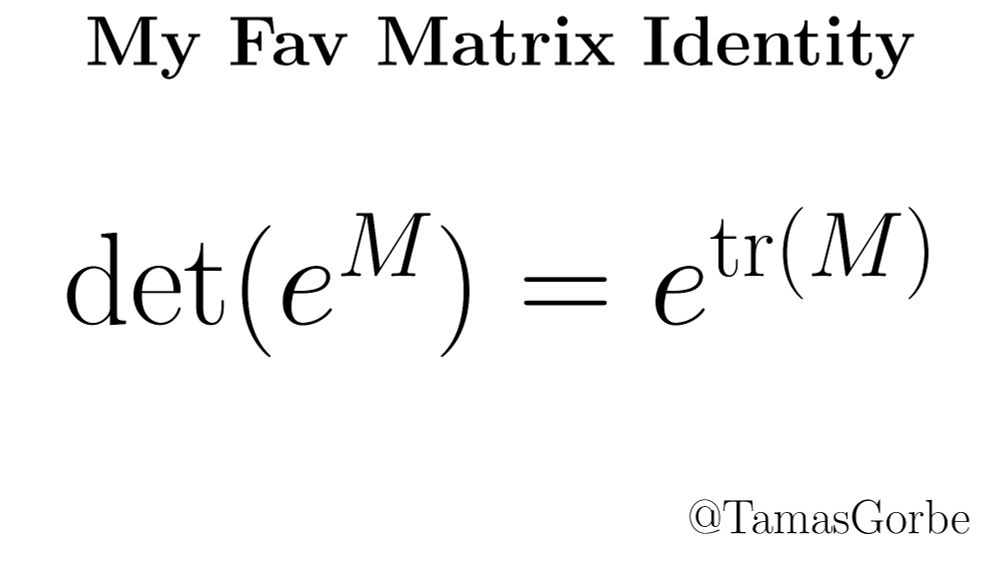
the determinant of the exponential equals the exponential of the trace

Having finite volume (π) and infinite(!) surface area, it leads to the apparent paradox:
"You can fill it with paint, but you cannot coat it."
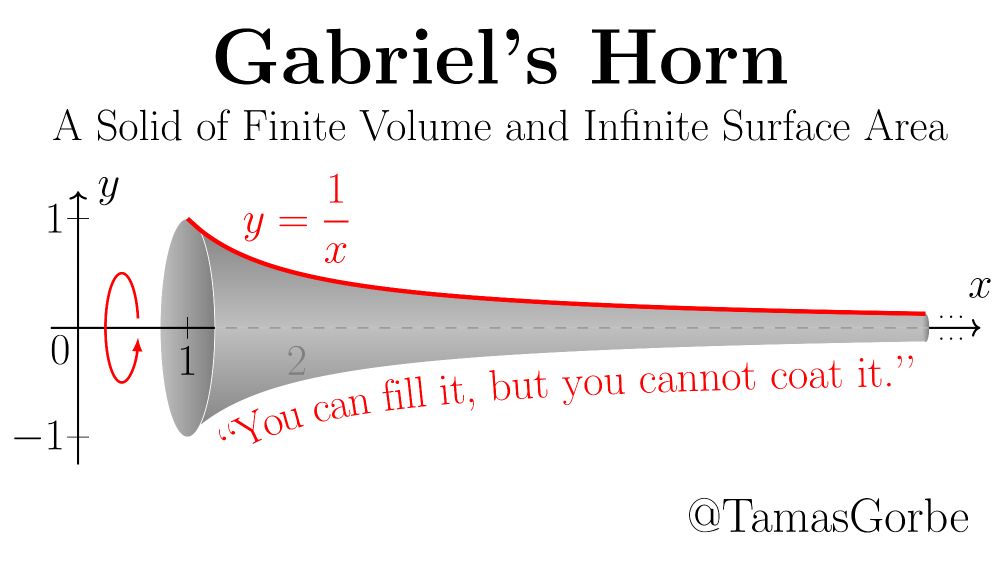
Having finite volume (π) and infinite(!) surface area, it leads to the apparent paradox:
"You can fill it with paint, but you cannot coat it."
Any square matrix cut from the top corner of Pascal's Triangle has determinant 1.

Any square matrix cut from the top corner of Pascal's Triangle has determinant 1.
f(x) = 1 / ( ⌊x⌋ + 1 − {x} )
and the sequence of numbers
0, f(0), −f(0), f(f(0)), −f(f(0)), f(f(f(0))), −f(f(f(0))), ...
Congratulations, you've just listed every rational number exactly once!
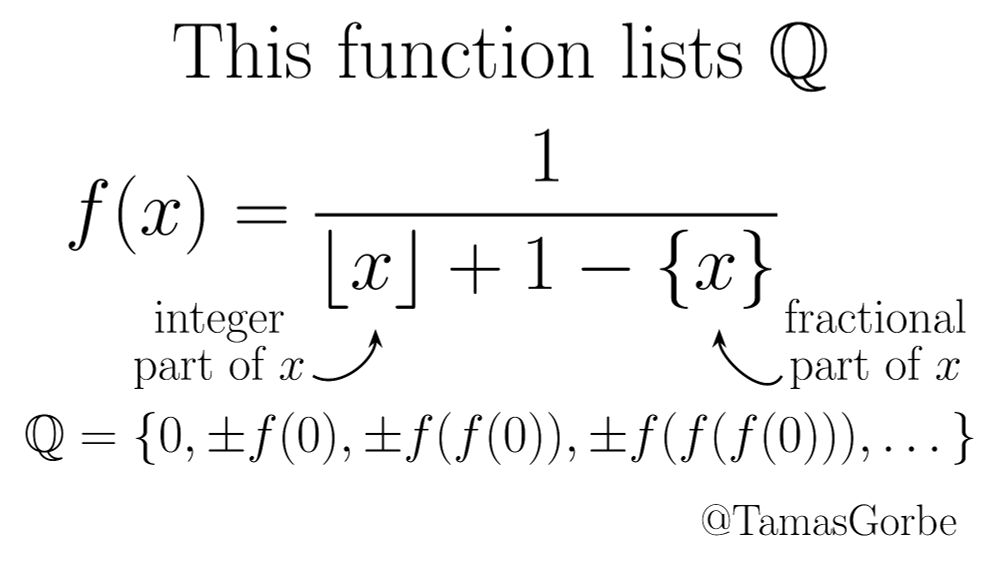
f(x) = 1 / ( ⌊x⌋ + 1 − {x} )
and the sequence of numbers
0, f(0), −f(0), f(f(0)), −f(f(0)), f(f(f(0))), −f(f(f(0))), ...
Congratulations, you've just listed every rational number exactly once!
− a visual proof −
sin(α+β) = sin(α)cos(β) + cos(α)sin(β)
cos(α+β) = cos(α)cos(β) – sin(α)sin(β)
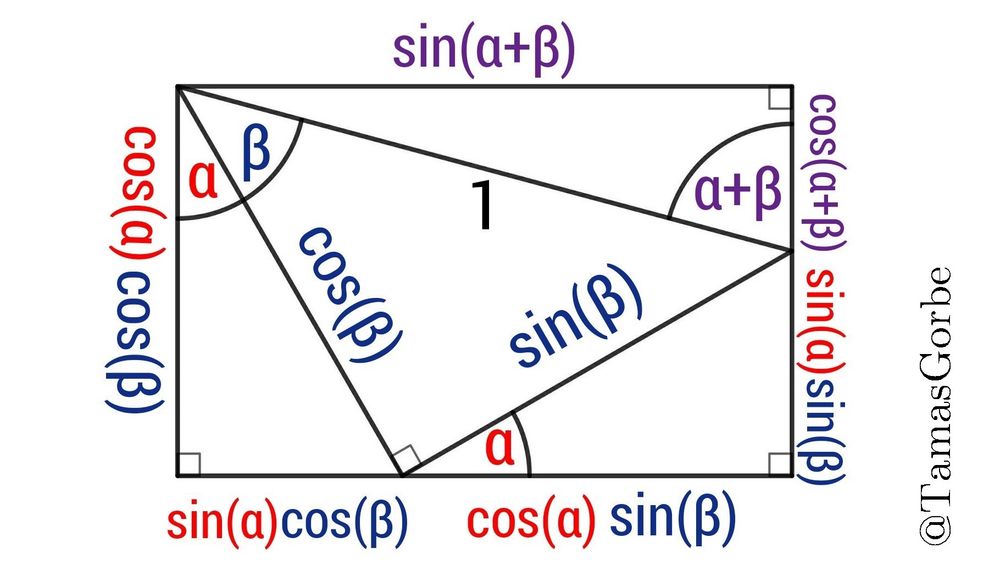
− a visual proof −
sin(α+β) = sin(α)cos(β) + cos(α)sin(β)
cos(α+β) = cos(α)cos(β) – sin(α)sin(β)
The ratio of the red arc and the blue focal segment is
√2 + ln(1+√2) = 2.29558...
for every parabola.
This is the universal parabolic constant, the “π of parabolas”.
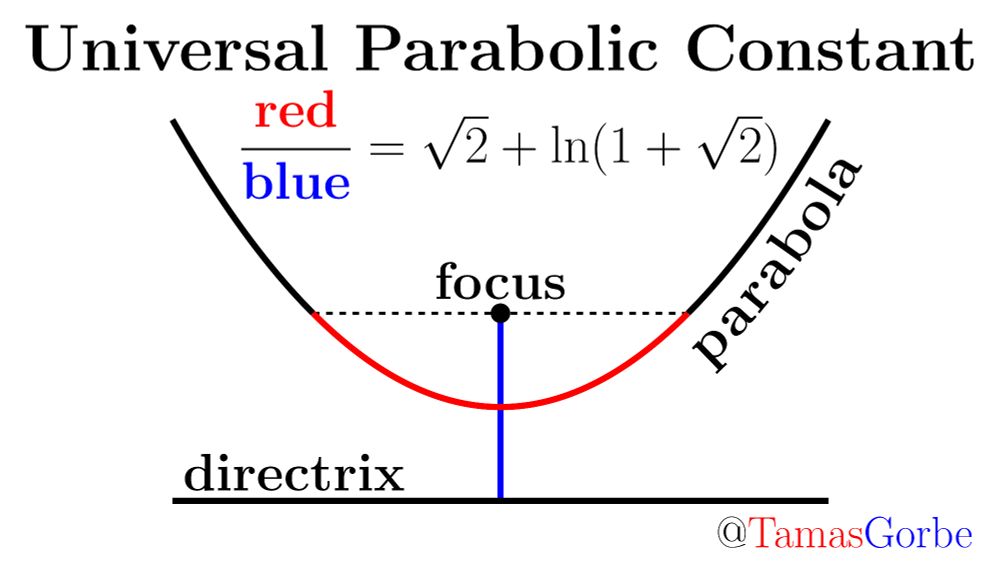
The ratio of the red arc and the blue focal segment is
√2 + ln(1+√2) = 2.29558...
for every parabola.
This is the universal parabolic constant, the “π of parabolas”.