With 132 participants, it was the first event of this scale to unite the research communities across all three fields – building bridges and allowing for new collaboration between areas that have traditionally developed independently. (2/4)

⚡ A favorite among participants: the lightning sessions, offering early-career researchers a stage to share ideas and connect.

The event was organized by Anna Wienhard, Freya Jensen, Levin Maier, Diaaeldin Taha, and Michael Bleher. (4/4)

🤝 Jointly organized by Max-Planck-Institut für Mathematik in den Naturwissenschaften and STRUCTURES Cluster of Excellence Heidelberg, the workshop featured inspiring keynote talks, expert presentations, and contributions from industry partners like DeepMind, Deepshore, and Isomorphic Labs. (3/4)

Topology, causality, mechanistic interpretability, it's all in there.

open.substack.com/pub/subthaum...

Happy for any reactions, confused or otherwise.

Surely it's "A monad in X is just a monoid in the category of endofunctors of X, with product × replaced by composition of endofunctors and unit set by the identity endofunctor."

The second article:

Looks at adiabatic solutions of the Haydys-Witten equations and relates them to paths in the moduli space of EBE monopoles. This suggests a relation between Haydys-Witten instanton Floer homology and symplectic Khovanov homology.

https://arxiv.org/abs/2501.01365

The first article:

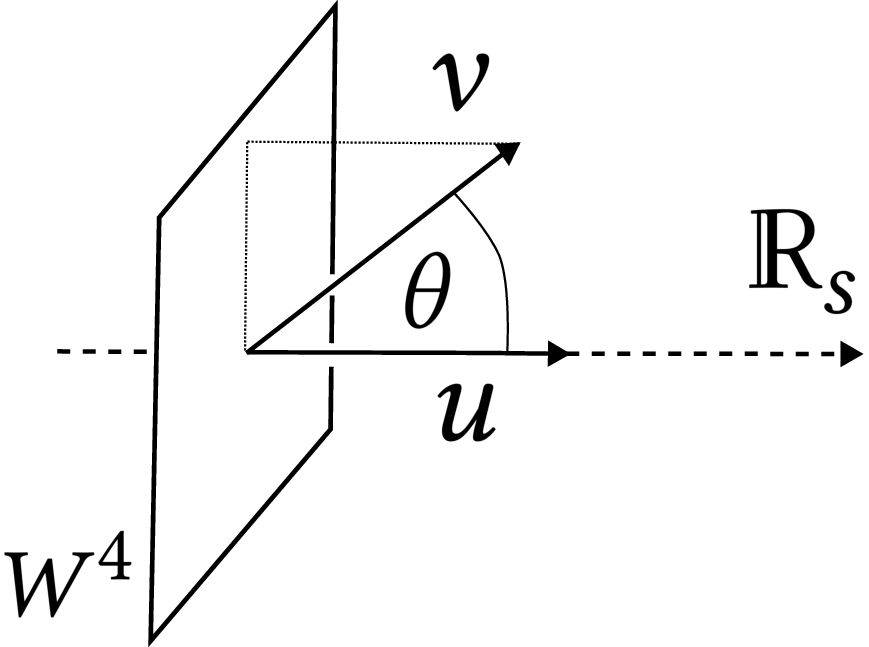
Introduces a one-parameter family of instanton Floer homology groups for four-manifolds, using the θ-Kapustin-Witten and Haydys-Witten equations. A conjecture by Witten links this to Khovanov homology for knots.

https://arxiv.org/abs/2412.13285

2/3