Thomas Steinke
@stein.ke
Computer science, math, machine learning, (differential) privacy
Researcher at Google DeepMind
Kiwi🇳🇿 in California🇺🇸
http://stein.ke/
Researcher at Google DeepMind
Kiwi🇳🇿 in California🇺🇸
http://stein.ke/
IMHO, the best analog to the AI bubble is the dotcom bubble. Yes, the internet proved to be economically transformative, but there was still a bubble. Companies made a lot of money in the end, but it wasn't necessarily the ones that people expected -- e.g., see CISCO:

October 9, 2025 at 1:17 AM
IMHO, the best analog to the AI bubble is the dotcom bubble. Yes, the internet proved to be economically transformative, but there was still a bubble. Companies made a lot of money in the end, but it wasn't necessarily the ones that people expected -- e.g., see CISCO:
🤦🤦🤦 this is not how two factor identification works 🤦🤦🤦🤦
![[Screenshot of an app]
Code Verification
Call customer service at 1-866-4220306 (outside the U.S. call 1-210-677-0065) to retrieve your One-time identification Code .](https://cdn.bsky.app/img/feed_thumbnail/plain/did:plc:thfnaqgktdwqbm42radc322i/bafkreiffo5kk6fobzmxoz3dnfwonqj36xejsutsj6wh6kuv4eqwzijh3gi@jpeg)
August 13, 2025 at 2:29 AM
🤦🤦🤦 this is not how two factor identification works 🤦🤦🤦🤦
Doing linear algebra in finite fields is fun because numerical instability doesn't exist. Alas, library support is limited, so you may find yourself writing your own Gaussian elimination.
![def modinv(a, p):
"""Computes inverse of a modulo p i.e. returns b such that (a*b)%p==1"""
u, v = a % p, p
x, y, w, z = 1, 0, 0, 1 # maintain ax+py==u and aw+pz==v
while u != 0: # extended Euclidean algorithm
q, r = v // u, v % u
x, y, w, z = w-qx, z-qy, x, y
u, v = r, u
if v != 1: return None # not invertible
return w % p
def modmatrixinverse(A, p):
"""Computes matrix inverse of A modulo p i.e. returns B s.t. A@B%p==I"""
A = numpy.array(A, dtype=int)
m, n = A.shape
assert m == n, "matrix must be square"
B = numpy.eye(n, dtype=int) # = nxn identity matrix
for i in range(n): # Gaussian elimination
b, j = None, i-1
while b is None:
j += 1
if j >= n: return None # not invertible
b = modinv(A[j,i], p)
if j > i: # swap rows i and j
A[j,:], A[i,:] = A[i,:], A[j,:]
B[j,:], B[i,:] = B[i,:], B[j,:]
A[i,:] = (A[i,:] * b) % p # divide A[i,:] by A[i,i]
B[i,:] = (B[i,:] * b) % p
for j in range(n): # zero out the rest of column i
if j != i:
B[j,:] = (B[j,:] - B[i,:] * A[j,i]) % p
A[j,:] = (A[j,:] - A[i,:] * A[j,i]) % p
return B](https://cdn.bsky.app/img/feed_thumbnail/plain/did:plc:thfnaqgktdwqbm42radc322i/bafkreifpv2rkjmgnwfgoaumjmxgv3gkd3rwufyinjvthca4dzcc2nbntwu@jpeg)
June 27, 2025 at 2:48 PM
Doing linear algebra in finite fields is fun because numerical instability doesn't exist. Alas, library support is limited, so you may find yourself writing your own Gaussian elimination.
What's the full acronym then? 🤔

May 22, 2025 at 8:19 PM
What's the full acronym then? 🤔
I'm a fan of the Jensen proof. It generalizes to prove Hölder's inequality:
![\textbf{H\"older's inequality from Jensen's inequality:}
\noindent
Let $x,y\in\mathbb{R}^d$ be arbitrary. Let $p,q \in (1,\infty)$ satisfy $\frac1p+\frac1q=1$. Without loss of generality, assume $x_i \ne 0$ for all $i \in [d]$.
Note that $v \mapsto |v|^p$ is convex.
For $i \in [d]$, define $u_i = |x_i|^q/\|x\|_q^q$ and $v_i = x_iy_i/|x_i|^q$. By Jensen's inequality,
\[\left|\frac{\sum_i x_i y_i}{\|x\|_q^q}\right|^p = \left|\sum_i u_i v_i\right|^p \le \sum_i u_i |v_i|^p = \frac{\sum_i |x_i|^{q+p-pq}|y_i|^p}{\|x\|_q^q} = \frac{\|y\|_p^p}{\|x\|_q^q}, \]
which rearranges to \[\left|\sum_i x_i y_i\right| \le \|x\|_q \cdot \|y\|_p.\]](https://cdn.bsky.app/img/feed_thumbnail/plain/did:plc:thfnaqgktdwqbm42radc322i/bafkreicxf5yshu7vcv6j625wl3ulltwhdsgxugxejil247ily2obs7n37i@jpeg)
May 14, 2025 at 6:06 PM
I'm a fan of the Jensen proof. It generalizes to prove Hölder's inequality:
Three proofs of Cauchy-Schwarz.
⟨x,y⟩ ≤ ∥x∥ ∥y∥
Are there any others you know of?
⟨x,y⟩ ≤ ∥x∥ ∥y∥
Are there any others you know of?

![\textbf{Jensen's inequality:}
\noindent
Let $x,y\in\mathbb{R}^d$ be arbitrary. Without loss of generality, assume $x_i \ne 0$ for all $i \in [d]$.
For $i \in [d]$, define $p_i = x_i^2/\|x\|^2$ and $v_i = y_i/x_i$. By Jensen's inequality,
\[\left(\frac{\sum_i x_i y_i}{\|x\|^2}\right)^2 = \left(\sum_i p_i v_i\right)^2 \le \sum_i p_i v_i^2 = \frac{\sum_i y_i^2}{\|x\|^2}, \]
which rearranges to \[\sum_i x_i y_i \le \|x\| \cdot \|y\|.\]](https://cdn.bsky.app/img/feed_thumbnail/plain/did:plc:thfnaqgktdwqbm42radc322i/bafkreiamyqso2lvlqbm35ryvp7ho7s2zelc4j4e23uefiopg44dj3yzqq4@jpeg)
![\textbf{Sum of squares:}
\noindent
Let $x,y\in\mathbb{R}^d$.
For all $\alpha,\beta>0$,
\[0 \le \| \alpha x - \beta y \|^2 = \alpha^2\|x\|^2 + \beta^2\|y\|^2 -2\alpha\beta\langle x , y \rangle\]
and, hence,
\[\langle x , y \rangle \le \frac{\alpha}{2\beta}\|x\|^2 + \frac{\beta}{2\alpha}\|y\|^2.\]
If $\|x\|=0$ or $\|y\|=0$, clearly $\langle x , y \rangle = 0$. Otherwise, set $\alpha=\|y\|$ and $\beta=\|x\|$ to obtain
\[\langle x , y \rangle \le \frac{\|y\|}{2\|x\|}\|x\|^2 + \frac{\|x\|}{2\|y\|}\|y\|^2 = \|x\| \cdot \| y \|.\]](https://cdn.bsky.app/img/feed_thumbnail/plain/did:plc:thfnaqgktdwqbm42radc322i/bafkreid3dwwigb4tczqgxa4hmdmtrzeucppw5ruvkd7tpcrlsc234f6kwi@jpeg)
May 14, 2025 at 6:06 PM
Three proofs of Cauchy-Schwarz.
⟨x,y⟩ ≤ ∥x∥ ∥y∥
Are there any others you know of?
⟨x,y⟩ ≤ ∥x∥ ∥y∥
Are there any others you know of?
Suppose X,Y,Z,W are independent standard Gaussians.
Then X·Y+W·Z has a standard Laplace distribution.
Similarly, Z·√(X^2+Y^2) has a standard Laplace distribution
Then X·Y+W·Z has a standard Laplace distribution.
Similarly, Z·√(X^2+Y^2) has a standard Laplace distribution

May 7, 2025 at 3:32 PM
Suppose X,Y,Z,W are independent standard Gaussians.
Then X·Y+W·Z has a standard Laplace distribution.
Similarly, Z·√(X^2+Y^2) has a standard Laplace distribution
Then X·Y+W·Z has a standard Laplace distribution.
Similarly, Z·√(X^2+Y^2) has a standard Laplace distribution
As an application of this, we get to prove concentrated differential privacy for the restricted Gaussian mechanism.
E.g. if you have a bounded query and add Gaussian noise, you can condition the noisy output to also be bounded without any loss in privacy parameters. 😁
E.g. if you have a bounded query and add Gaussian noise, you can condition the noisy output to also be bounded without any loss in privacy parameters. 😁

April 27, 2025 at 1:38 AM
As an application of this, we get to prove concentrated differential privacy for the restricted Gaussian mechanism.
E.g. if you have a bounded query and add Gaussian noise, you can condition the noisy output to also be bounded without any loss in privacy parameters. 😁
E.g. if you have a bounded query and add Gaussian noise, you can condition the noisy output to also be bounded without any loss in privacy parameters. 😁
Here's an application using the Log Sobolev Inequality for strongly log-concave distributions to bound KL divergence which can thus be converted to a bound on Rényi divergence.

April 27, 2025 at 1:36 AM
Here's an application using the Log Sobolev Inequality for strongly log-concave distributions to bound KL divergence which can thus be converted to a bound on Rényi divergence.
You can bound Rényi divergences in terms of KL divergences for tilted distributions. This is useful e.g. for Gaussians, where tilting just corresponds to shifting the distribution.

April 26, 2025 at 8:03 PM
You can bound Rényi divergences in terms of KL divergences for tilted distributions. This is useful e.g. for Gaussians, where tilting just corresponds to shifting the distribution.
There are also rod cells in your retina. In principle these give you a 4th dimension for perceiving colour. But they are for peripheral & night vision, so we don't perceive a 4th color dimension. 🤷

April 19, 2025 at 10:20 PM
There are also rod cells in your retina. In principle these give you a 4th dimension for perceiving colour. But they are for peripheral & night vision, so we don't perceive a 4th color dimension. 🤷
Colours correspond to infinite-dimensional vectors, since there are infinitely many wavelengths of light.
But humans can only perceive a three-dimensional projection of colour (red, green, & blue).
What's interesting is that it's *not* an orthogonal projection. Here's a plot of the basis vectors.
But humans can only perceive a three-dimensional projection of colour (red, green, & blue).
What's interesting is that it's *not* an orthogonal projection. Here's a plot of the basis vectors.
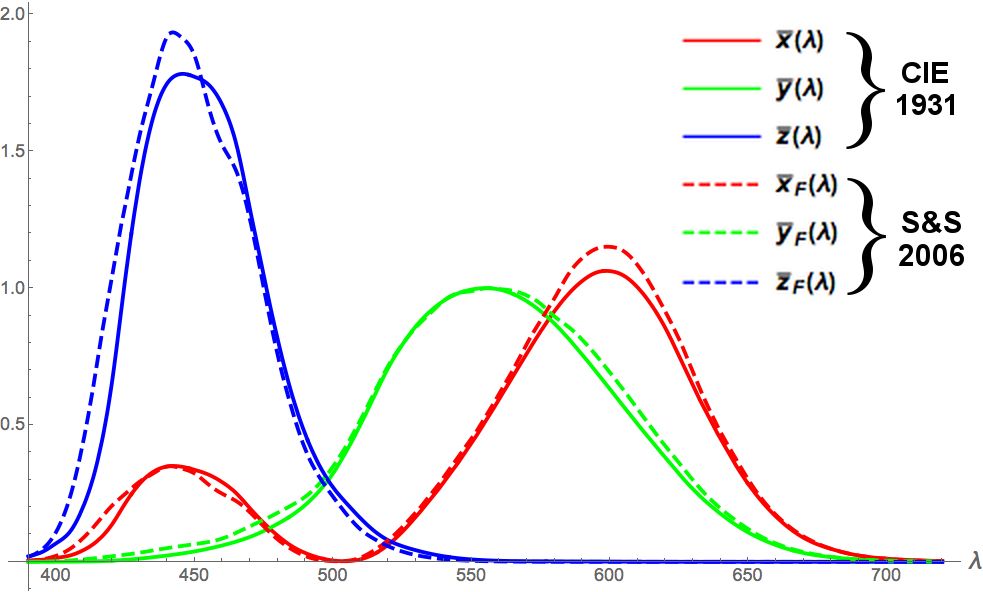
April 19, 2025 at 10:12 PM
Colours correspond to infinite-dimensional vectors, since there are infinitely many wavelengths of light.
But humans can only perceive a three-dimensional projection of colour (red, green, & blue).
What's interesting is that it's *not* an orthogonal projection. Here's a plot of the basis vectors.
But humans can only perceive a three-dimensional projection of colour (red, green, & blue).
What's interesting is that it's *not* an orthogonal projection. Here's a plot of the basis vectors.
Taking α→1 gives a triangle inequality for KL divergence. This can also be proved using my favourite lemma. 😁
![Full LaTeX source: https://pastebin.com/mA6KjUJs
\begin{proposition}[Triangle-like inequality for KL divergence]\label{prop:kl-triangle}
Let $P$, $R$, and $Q$ be probability distributions with $P$ being absolutely continuous with respect to $R$ and $R$ being absolutely conotinuous with respect to $Q$.
Let $\kappa \in (1,\infty)$.
Then
\[
\dr{\text{KL}}{P}{Q} \le \frac{\kappa}{\kappa-1} \dr{\text{KL}}{P}{R} + \dr{\kappa}{R}{Q},
\]
where $\dr{\text{KL}}{P}{Q} := \ex{X \gets P}{\log(P(X)/Q(X)}$ denotes the KL divergence and\\$\dr{\kappa}{R}{Q} = \frac{1}{\kappa-1} \log \ex{X \gets R}{(R(X)/Q(X))^{\kappa-1}}$ denotes the R\'enyi divergence of order $\kappa$.
\end{proposition}](https://cdn.bsky.app/img/feed_thumbnail/plain/did:plc:thfnaqgktdwqbm42radc322i/bafkreibz3gfiqvyvbld7jgfnb6kzac2j6qrxirofpwrxiv5mpz6j7r6md4@jpeg)
April 19, 2025 at 5:44 PM
Taking α→1 gives a triangle inequality for KL divergence. This can also be proved using my favourite lemma. 😁
Renyi divergences satisfy a triangle inequality (with an extra multiplier).
The proof boils down to Holder's inequality.
The proof boils down to Holder's inequality.

April 19, 2025 at 5:44 PM
Renyi divergences satisfy a triangle inequality (with an extra multiplier).
The proof boils down to Holder's inequality.
The proof boils down to Holder's inequality.
Here's a very simple calculation showing that adding a bit of randomization can make numerical integration better even in the one-dimensional setting.

April 4, 2025 at 6:27 PM
Here's a very simple calculation showing that adding a bit of randomization can make numerical integration better even in the one-dimensional setting.
Rather than a uniform bound (a.k.a. Kolmogorov–Smirnov distance), we can also get a universal multiplicative bound. This is tighter in the tails of the distribution.

March 29, 2025 at 5:08 PM
Rather than a uniform bound (a.k.a. Kolmogorov–Smirnov distance), we can also get a universal multiplicative bound. This is tighter in the tails of the distribution.
The DKW inequality states that, given i.i.d. samples from a univariate distribution, with high probability the empirical CDF is *uniformly* close to the true CDF.
The uniform guarantee is as tight as the pointwise guarantee.
(Alas I couldn't get this proof down to 1 page. 😅 )
The uniform guarantee is as tight as the pointwise guarantee.
(Alas I couldn't get this proof down to 1 page. 😅 )


March 29, 2025 at 5:08 PM
The DKW inequality states that, given i.i.d. samples from a univariate distribution, with high probability the empirical CDF is *uniformly* close to the true CDF.
The uniform guarantee is as tight as the pointwise guarantee.
(Alas I couldn't get this proof down to 1 page. 😅 )
The uniform guarantee is as tight as the pointwise guarantee.
(Alas I couldn't get this proof down to 1 page. 😅 )
The quotient rule for higher derivatives is not as messy as I feared. 😅
And the matrix is lower-triangular, so it's easy to invert.
And the matrix is lower-triangular, so it's easy to invert.
![LaTeX source: https://pastebin.com/qtw8DPh8
\begin{lemma}[Quotient Rule for Higher Derivatives] ~\\
Let $h(x) := \frac{f(x)}{g(x)}$ with $g(x) \ne 0$. Then, %$h'(x) = \frac{f'(x)g(x)-f(x)g'(x)}{g(x)^2}$. More generally,
for all $n \in \mathbb{N}$,
\[
\left(\begin{array}{c}
h(x) \\
h'(x) \\
h''(x) \\
h'''(x) \\
\vdots \\
h^{(k)}(x) \\
\vdots \\
h^{(n-1)}(x)
\end{array}\right)
=
\left(\begin{array}{ccccc}
g(x) & 0 & 0 & \cdots & 0 \\
g'(x) & g(x) & 0 & \cdots & 0 \\
g''(x) & 2 g'(x) & g(x) & \cdots & 0 \\
g'''(x) & 3 g''(x) & 3 g'(x) & \cdots & 0 \\
\vdots & \vdots & \vdots & \ddots & 0 \\
g^{(k)}(x) & {k \choose 1} g^{(k-1)}(x) & {k \choose 2} g^{(k-2)}(x) & \cdots & 0 \\
\vdots & \vdots & \vdots & \ddots & 0 \\
g^{(n-1)}(x) & {n-1 \choose 1} g^{(n-2)}(x) & {n-1 \choose 2} g^{(n-3)}(x) & \cdots & g(x)
\end{array}\right)^{-1}
\left(\begin{array}{c}
f(x) \\
f'(x) \\
f''(x) \\
f'''(x) \\
\vdots \\
f^{(k)}(x) \\
\vdots \\
f^{(n-1)}(x)
\end{array}\right) .
\]
\end{lemma}](https://cdn.bsky.app/img/feed_thumbnail/plain/did:plc:thfnaqgktdwqbm42radc322i/bafkreidykasrfyvrd4w77drvh2wesxkxkqmswvvzom5fzm27p7wb7da7fe@jpeg)
March 27, 2025 at 3:20 PM
The quotient rule for higher derivatives is not as messy as I feared. 😅
And the matrix is lower-triangular, so it's easy to invert.
And the matrix is lower-triangular, so it's easy to invert.
L.J. Mordell effectively republished the formula in 1933. This paper is available. In it he laments that his 1920 paper is not well known.
doi.org/10.1007/BF02...
doi.org/10.1007/BF02...

March 26, 2025 at 3:41 PM
L.J. Mordell effectively republished the formula in 1933. This paper is available. In it he laments that his 1920 paper is not well known.
doi.org/10.1007/BF02...
doi.org/10.1007/BF02...
This formula is known as the Mordell integral.
If you try looking up Mordell's original paper from 1920, you get nothing: 🙃
If you try looking up Mordell's original paper from 1920, you get nothing: 🙃
![creenshot from Google Scholar with the followng text. But no link to the paper.
[CITATION] The value of the definite integral∫∞−∞ eat2+ bt ect+ d dt
LJ Mordell - Quarterly J. of Math, 1920
Save Cite Cited by 35 Related articles](https://cdn.bsky.app/img/feed_thumbnail/plain/did:plc:thfnaqgktdwqbm42radc322i/bafkreif65lvthgv7ln6q6xxgdtf3wrl5sollmu5q6e7i7f2hd7qvyhyreu@jpeg)
March 26, 2025 at 3:41 PM
This formula is known as the Mordell integral.
If you try looking up Mordell's original paper from 1920, you get nothing: 🙃
If you try looking up Mordell's original paper from 1920, you get nothing: 🙃
I don't know how someone came up with this crazy formula for the mean of a logit-Normal, but I'm glad they did. It converges extremely fast.
en.wikipedia.org/wiki/Logit-n...
en.wikipedia.org/wiki/Logit-n...
![\begin{proposition}[Mean of Logit-Normal Distribution]
For all $\mu\in\mathbb{R}$ and all $\sigma>0$,
\begin{align*}
&\ex{X \gets \mathcal{N}(\mu,\sigma^2)}{\frac{1}{1+e^{-X}}} = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^\infty \frac{1}{1+e^{-(\mu+\sigma x)}} e^{-x^2/2} \mathrm{d}x \\
&= \frac12 + \frac{\sum_{n=1}^\infty e^{-\sigma^2n^2/2} \sinh(n\mu)\tanh(n\sigma^2/2) + \frac{2\pi}{\sigma^2} e^{-(2n-1)^2\pi^2/2\sigma^2} \frac{\sin((2n-1)\pi\mu/\sigma^2)}{\sinh((2n-1)\pi^2/\sigma^2)}}{1 + 2 \sum_{m=1}^\infty e^{-\sigma^2m^2/2} \cosh(m\mu)}
\end{align*}
\end{proposition}](https://cdn.bsky.app/img/feed_thumbnail/plain/did:plc:thfnaqgktdwqbm42radc322i/bafkreiah5ittkezmk46nyanv7imc2ha6c6klzuqvh5nj7fx33w5rsl4gxi@jpeg)
March 26, 2025 at 3:41 PM
I don't know how someone came up with this crazy formula for the mean of a logit-Normal, but I'm glad they did. It converges extremely fast.
en.wikipedia.org/wiki/Logit-n...
en.wikipedia.org/wiki/Logit-n...
Integration is to differentiation as NP is to P.
![\begin{theorem}
For all $c>1$, \[\frac{1}{2\pi} \int_{-\pi}^{\pi} \frac{1}{c+\sin(\theta)} \mathrm{d} \theta = \frac{1}{\sqrt{c^2-1}}.\]
\end{theorem}
\begin{proof}
Clearly
\[\frac{\mathrm{d}}{\mathrm{d}\theta} \left[ \frac{2}{\sqrt{c^2-1}} \tan^{-1}\left(\frac{1 + c \tan (\theta/2)}{\sqrt{c^2-1}}\right) \right] = \frac{1}{c+\sin(\theta)}.\]
The result now follows from the fundamental theorem of calculus.
\end{proof}](https://cdn.bsky.app/img/feed_thumbnail/plain/did:plc:thfnaqgktdwqbm42radc322i/bafkreih422niyuwsosyjc5yndqxohza3mo5snurp4vofn4g54igvqi3icu@jpeg)
March 25, 2025 at 4:48 PM
Integration is to differentiation as NP is to P.
Upper bounds like this are particularly useful, e.g., if you need to bound the expectation E[log(1+exp(X))].
This bound is a reformulation of Proposition 4.1 of arxiv.org/abs/1901.09188
or Equation 1.3 in
doi.org/10.1214/ECP....
This bound is a reformulation of Proposition 4.1 of arxiv.org/abs/1901.09188
or Equation 1.3 in
doi.org/10.1214/ECP....

March 24, 2025 at 4:26 PM
Upper bounds like this are particularly useful, e.g., if you need to bound the expectation E[log(1+exp(X))].
This bound is a reformulation of Proposition 4.1 of arxiv.org/abs/1901.09188
or Equation 1.3 in
doi.org/10.1214/ECP....
This bound is a reformulation of Proposition 4.1 of arxiv.org/abs/1901.09188
or Equation 1.3 in
doi.org/10.1214/ECP....
This is known as the Kearns-Saul inequality, which improves Hoeffding's lemma. It gives the optimal constant (independent of a) coefficient for the quadratic term.
It matches the Taylor series in constant & linear terms.
See how the upper bound compares to the 2nd-order Taylor series:
It matches the Taylor series in constant & linear terms.
See how the upper bound compares to the 2nd-order Taylor series:



![Quadratic upper bound:
\[\log(1+e^x) \le \log(1+e^a) + \frac{x-a}{1+e^{-a}} + \frac{(e^a-1) \cdot (x-a)^2}{4 \cdot a \cdot (e^a+1)}.\]
Second-order Taylor series:
\[\log(1+e^x) \approx \log(1+e^a) + \frac{x-a}{1+e^{-a}} + \frac{ (x-a)^2}{2 \cdot (e^a+2+e^{-a})}.\]](https://cdn.bsky.app/img/feed_thumbnail/plain/did:plc:thfnaqgktdwqbm42radc322i/bafkreiavhqrcp6wbdnkq2okzgztstquqbz36vk4gzq4g432z2leoi4kauu@jpeg)
March 24, 2025 at 4:26 PM
This is known as the Kearns-Saul inequality, which improves Hoeffding's lemma. It gives the optimal constant (independent of a) coefficient for the quadratic term.
It matches the Taylor series in constant & linear terms.
See how the upper bound compares to the 2nd-order Taylor series:
It matches the Taylor series in constant & linear terms.
See how the upper bound compares to the 2nd-order Taylor series:


