
www.simontoussaint.nl
My dissertation can be found here: research-portal.uu.nl/en/publicati...

My dissertation can be found here: research-portal.uu.nl/en/publicati...



Happily, my adjusted returns do show a steep & positive gradient, consistent with theory 14/

Happily, my adjusted returns do show a steep & positive gradient, consistent with theory 14/
Top wealth shares also increase strongly: here are the adjusted top 1% shares. They increase by 3-5 pp on average. Top 0.1% also increase by this amount 12/

Top wealth shares also increase strongly: here are the adjusted top 1% shares. They increase by 3-5 pp on average. Top 0.1% also increase by this amount 12/
My estimates do not suffer from this 11/

My estimates do not suffer from this 11/
We see that my procedure is necessary; simply using an initial estimate (green) is insufficient 10/

We see that my procedure is necessary; simply using an initial estimate (green) is insufficient 10/
8/

8/
Then, fitted values from this IV/GMM regression will be error-free market values 7/

Then, fitted values from this IV/GMM regression will be error-free market values 7/
But this is 2 equations in 2 unknowns (β and variance of ξ)! Intuitively, the differences in bias betw the regs gives identifying information 6/
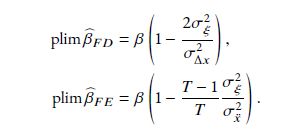
But this is 2 equations in 2 unknowns (β and variance of ξ)! Intuitively, the differences in bias betw the regs gives identifying information 6/
But this holds more generally: I show that even when firms have markups and/or decreasing returns to scale, firm value is approx linear in their capital stock
4/
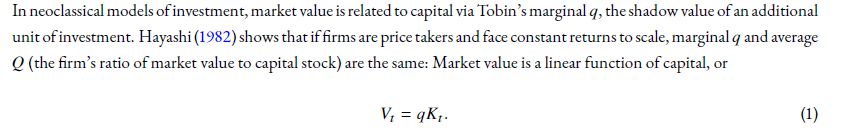
But this holds more generally: I show that even when firms have markups and/or decreasing returns to scale, firm value is approx linear in their capital stock
4/
Private businesses make up 50% of sales & profits and are the main wealth component of the wealthiest households. So, what is their value? Well, that's difficult, since they're not listed: their value is unobservable by definition!
My #EconJMP tackles this problem 1/
![Robust Estimation of Private Business Wealth*
Job Market Paper
Simon J. Toussaint†
November 14, 2024
[Most recent version here]
Abstract
Estimating the market value of private businesses is essential for understanding both aggregate firm dynamics and top wealth
inequality, yet these values are inherently unobservable. This paper introduces an econometric approach that treats the gap
between true market values and initial estimates as measurement error. I employ time-series restrictions on these errors as
moment conditions within a GMM framework, and use the fitted values from these estimations as error-free estimates of
private business wealth and capital stocks. Applying this method to Dutch administrative data linking the universe of firms
to their owners, I find that aggregate private business wealth increases by 30% of GDP initially, and is more stable than the
unadjusted series. Top 1% and 0.1% wealth shares increase by 3–5 percentage points, peaking at 38% and 20%, respectively.
Adjusted returns to firm wealth exhibit a steeper gradient across the wealth distribution than unadjusted returns, consistent
with models of return heterogeneity.](https://cdn.bsky.app/img/feed_thumbnail/plain/did:plc:wus4g34bpbzjefp547irpkeu/bafkreibg34g2k7zwmjqytkllrcxfsj5tnov22hdny74qz7ks5jwa5csbou@jpeg)
Private businesses make up 50% of sales & profits and are the main wealth component of the wealthiest households. So, what is their value? Well, that's difficult, since they're not listed: their value is unobservable by definition!
My #EconJMP tackles this problem 1/

Very special to catch a Yo-Yo Ma concert this evening, finally seeing him live!

Very special to catch a Yo-Yo Ma concert this evening, finally seeing him live!


How to use this? E.g. City size must be bounded by area already used 7/

How to use this? E.g. City size must be bounded by area already used 7/
The table shows 1) Weibull does extremely well; 2) Pareto fails miserably, with infinite and nonsensically large values in majority of cases 6/

The table shows 1) Weibull does extremely well; 2) Pareto fails miserably, with infinite and nonsensically large values in majority of cases 6/

R_k should equal 1 if W is Pareto; this is our (sharp) test. See the values of R_2 and R_3 for firm size below: Clearly not equal to 1 (same for wealth & city size).
3/

R_k should equal 1 if W is Pareto; this is our (sharp) test. See the values of R_2 and R_3 for firm size below: Clearly not equal to 1 (same for wealth & city size).
3/
Coen Teulings and I study three distributions (wealth, city and firm size), which are always thought to be distributed Pareto.
Bottom line: These distributions are *not* Pareto, but Weibull! A thread 1/

Coen Teulings and I study three distributions (wealth, city and firm size), which are always thought to be distributed Pareto.
Bottom line: These distributions are *not* Pareto, but Weibull! A thread 1/


