https://people.math.wisc.edu/~spagnolie/


www.colorado.edu/conference/b...

www.colorado.edu/conference/b...


ncses.nsf.gov/pubs/nsb2025...

ncses.nsf.gov/pubs/nsb2025...








elasticity, since these contribute to larger LC deformations, which (as above) hinder particle transport. (Pe_s: Peclet #) 18/20



elasticity, since these contribute to larger LC deformations, which (as above) hinder particle transport. (Pe_s: Peclet #) 18/20





journals.aps.org/prl/abstract...

journals.aps.org/prl/abstract...
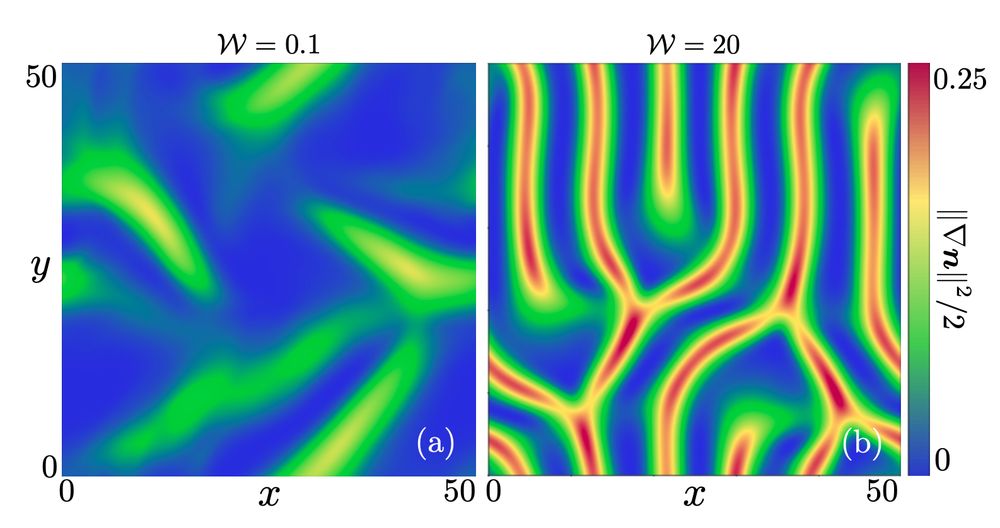
needed to trigger a nontrivial state is also lower, intuitively. 11/20

needed to trigger a nontrivial state is also lower, intuitively. 11/20