


この式は、ドルコスト平均法で正の値(1+w*sin(x))で単振動する投資信託を微小時間あたり1dx円ずつ購入した場合、1周期経過後には、2π円の購入コストがかかっているが、実際には 2π/(√(1−w^2))円の評価額になっており、実際にはプラス運用になることを示します。株価がフーリエ級数だと仮定すると、株価が上昇せずボックス相場であったとしても、プラス運用になります。ただし、1周期の途中で取りやめた場合は除外。w=株価に対する振幅比は大きい方が効果が高く、例えばリーマンショックのような50%を経験した後の評価額は、2/(√3)倍になります。
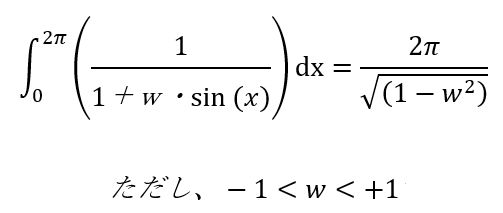
この式は、ドルコスト平均法で正の値(1+w*sin(x))で単振動する投資信託を微小時間あたり1dx円ずつ購入した場合、1周期経過後には、2π円の購入コストがかかっているが、実際には 2π/(√(1−w^2))円の評価額になっており、実際にはプラス運用になることを示します。株価がフーリエ級数だと仮定すると、株価が上昇せずボックス相場であったとしても、プラス運用になります。ただし、1周期の途中で取りやめた場合は除外。w=株価に対する振幅比は大きい方が効果が高く、例えばリーマンショックのような50%を経験した後の評価額は、2/(√3)倍になります。

これの特徴的なのは、従来型4%運用固定方式と違い、FIRE前のアセットアロケーションとFIRE後のアセットアロケーションに応じてより柔軟に運用効率を設定できることです。
今数式をあらためてみると、N(苦痛な労働年数)がLossに見え、p,q,sに勾配があるように見えてしまうのです。
なんだか、FIREオタクとAIオタクという関係ない話が急につながってきて面白いです。

これの特徴的なのは、従来型4%運用固定方式と違い、FIRE前のアセットアロケーションとFIRE後のアセットアロケーションに応じてより柔軟に運用効率を設定できることです。
今数式をあらためてみると、N(苦痛な労働年数)がLossに見え、p,q,sに勾配があるように見えてしまうのです。
なんだか、FIREオタクとAIオタクという関係ない話が急につながってきて面白いです。






















