






arxiv.org/abs/1601.01694

arxiv.org/abs/1601.01694
As you can see, I was also very busy pensively staring at Platonic solids at the Hungarian National Museum.

As you can see, I was also very busy pensively staring at Platonic solids at the Hungarian National Museum.
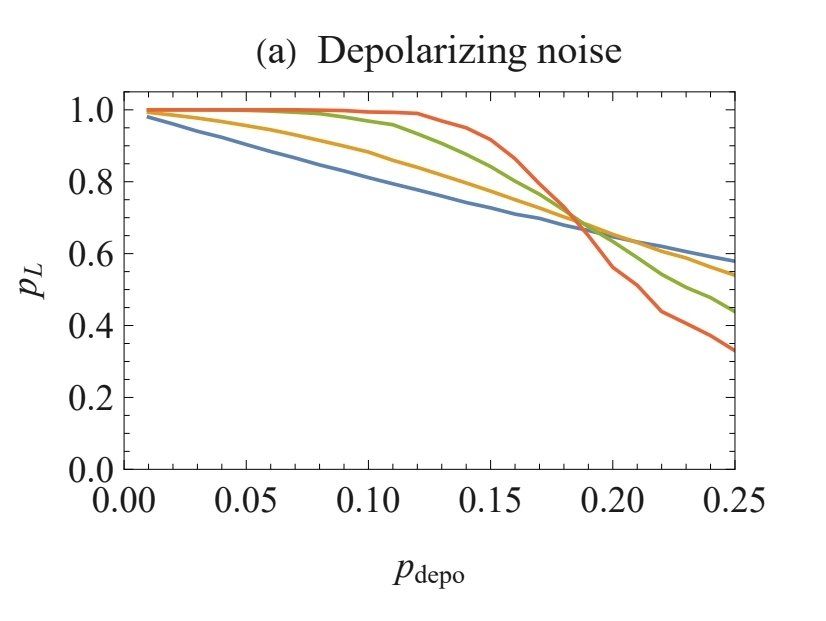
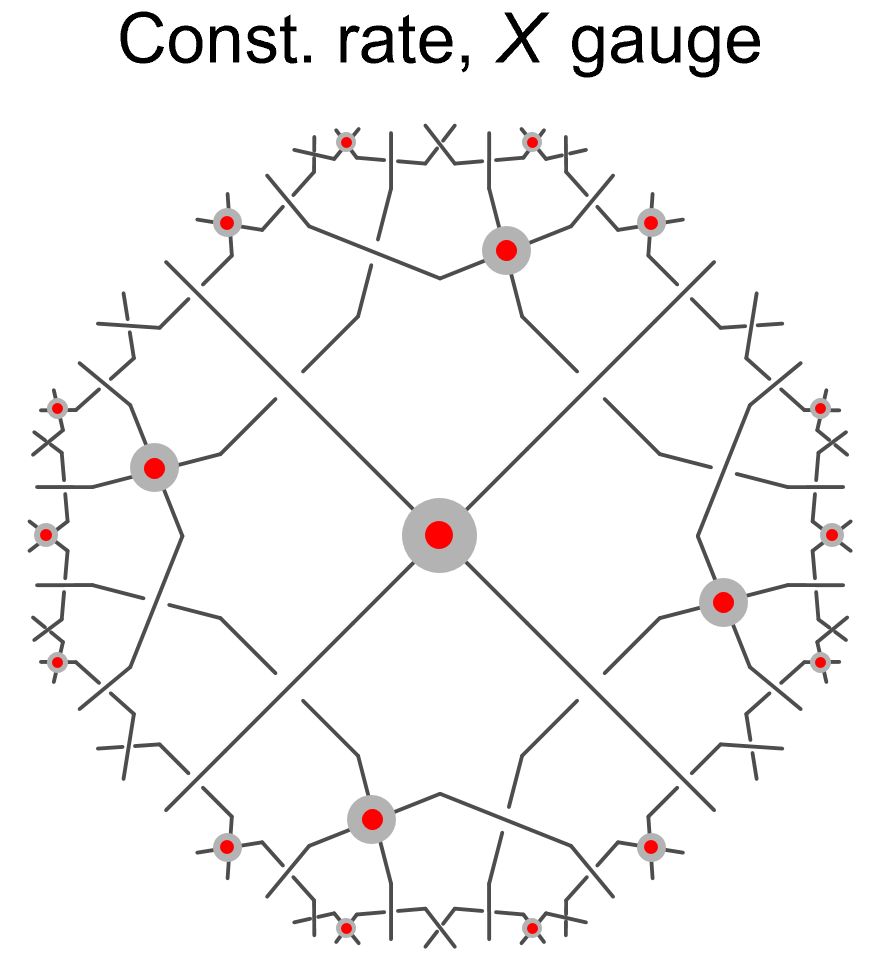

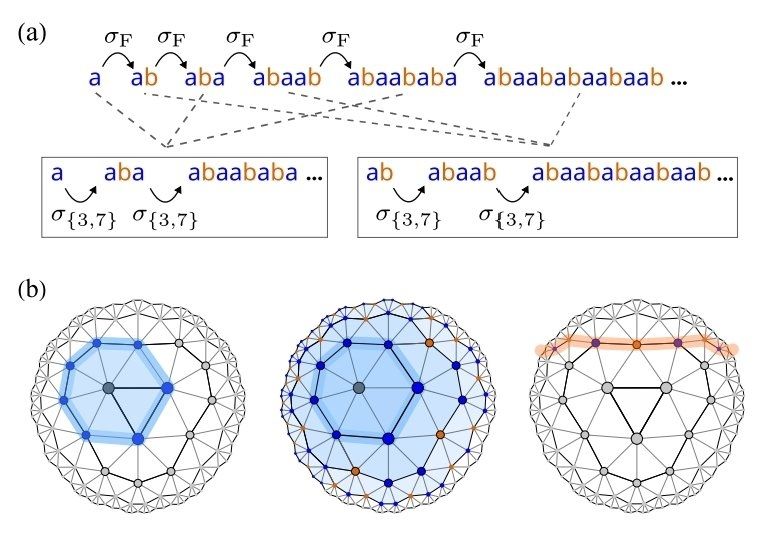
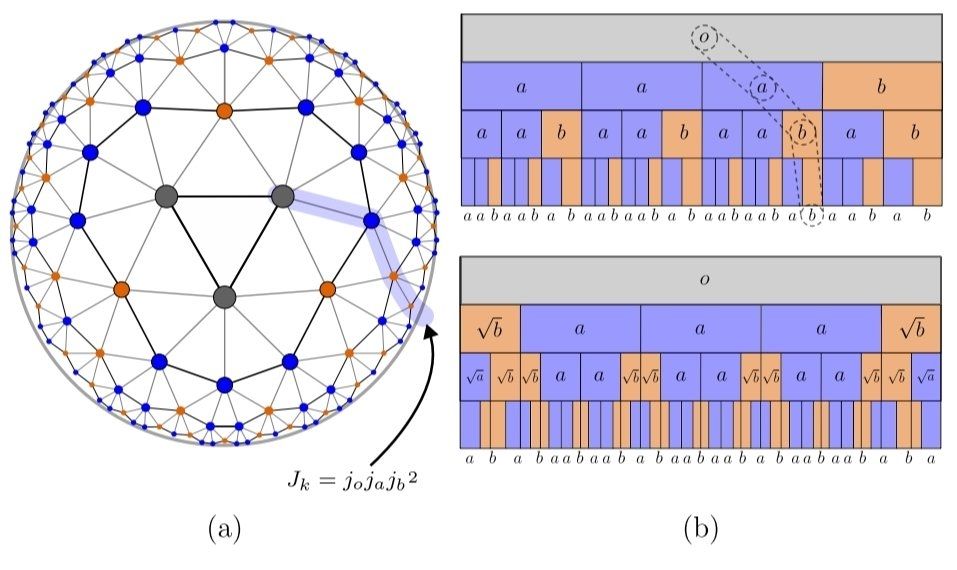
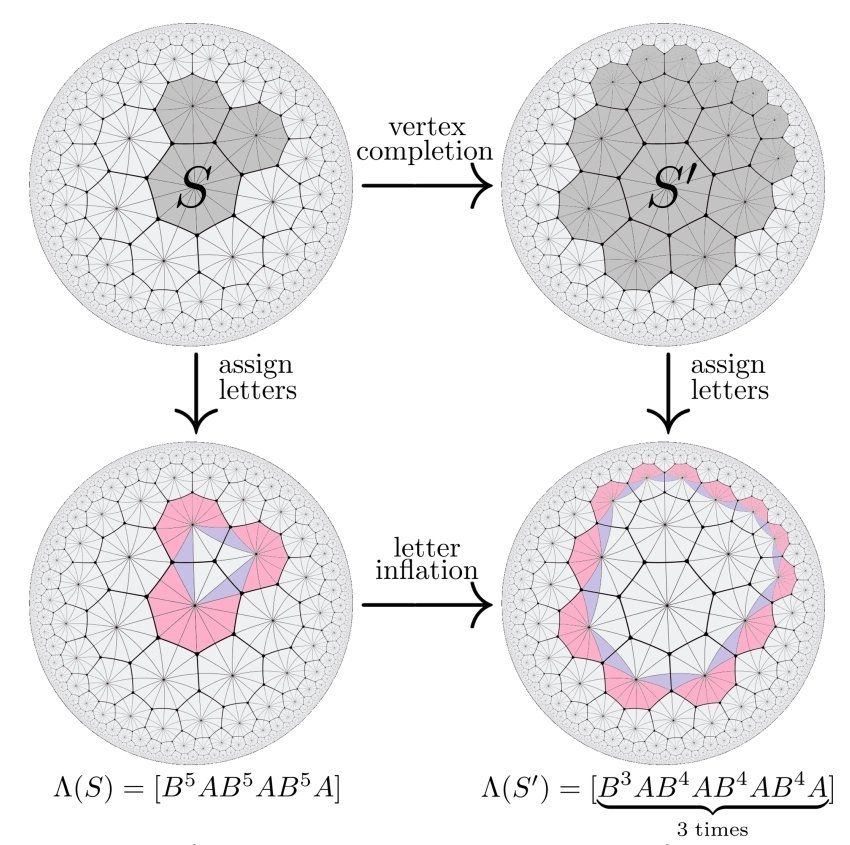
We explore the symmetries of discrete-holographic models and find that they generically produce critical phases in spin systems - but only when the symmetries describe a "dual" bulk geometry!

We explore the symmetries of discrete-holographic models and find that they generically produce critical phases in spin systems - but only when the symmetries describe a "dual" bulk geometry!
He's the main driver behind our work on von Neumann algebras in infinite tensor networks from April, see thread below.

He's the main driver behind our work on von Neumann algebras in infinite tensor networks from April, see thread below.
Lenny Susskind started his opening talk on de Sitter holography in classic Lenny Susskind style:
"Hello children."

Lenny Susskind started his opening talk on de Sitter holography in classic Lenny Susskind style:
"Hello children."



arxiv.org/abs/2102.02619

arxiv.org/abs/2102.02619



Why is that surprising? Well...
arxiv.org/abs/2504.10386

Why is that surprising? Well...
arxiv.org/abs/2504.10386

