Finally, this work would not have been possible without the excellent collaborators Song Wen, Dimitris N. Metaxas, and
Yezhou Yang.

We would also like to thank the SCAI ASU, ASU Research Computing, and cr8dl.ai for generous support w.r.t. GPUs.

We’re thrilled to release FlowChef on InstaFlow and Flux.1[dev] models for the community to explore and experiment with! 🌟

Project Page: flowchef.github.io
Demo on Flux: huggingface.co/spaces/FlowC...
Demo on InstaFlow: huggingface.co/spaces/FlowC...

Dive in and let us know what you think! ✨

We show an extension to 3D and multi-subject editing! 🤯🤯

However, we believe such a straightforward and impactful method could benefit downstream tasks such as video generation. 🚀

🎨 Extending FlowChef for Image Editing

We take FlowChef a step further: enabling image editing without performing an inversion of the source image! 🚀

🔥 Even more exciting, this is one of the first approaches to achieve SOTA results on Flux.

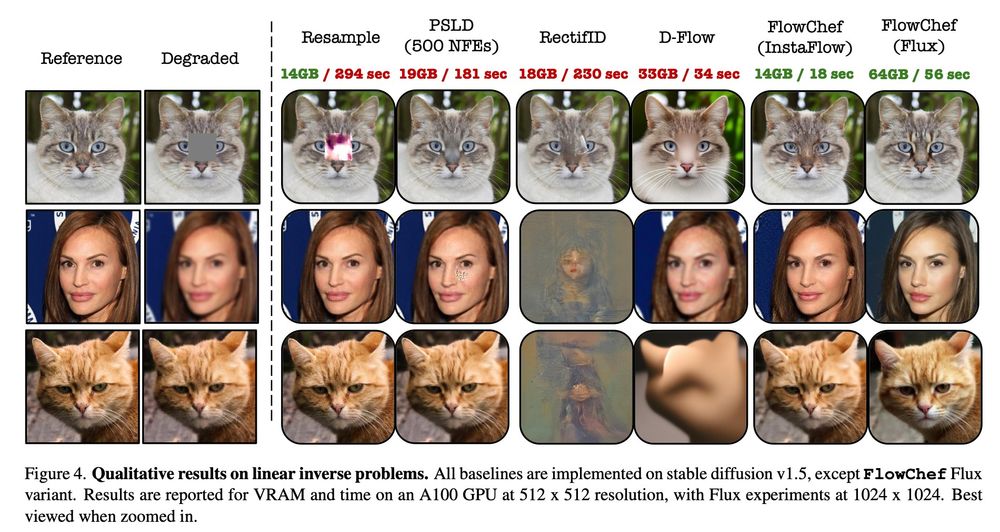
On inverse problems, our method achieves SOTA performance while being the most efficient approach! 💪

Plus, it’s versatile: seamlessly applicable to both pixel and latent space models. 🤯

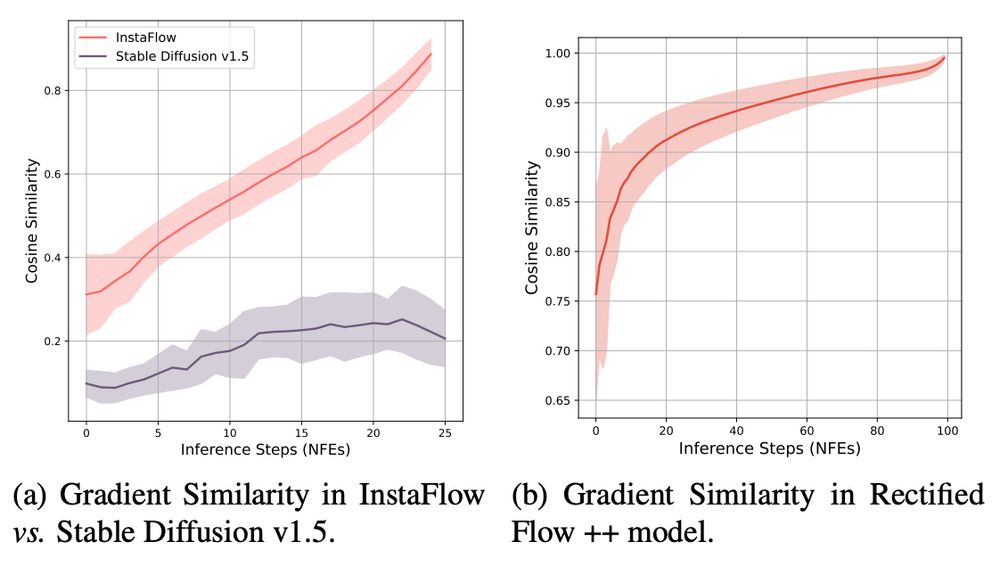
🎯 Our theoretical insights are backed by empirical observations!

💡 As t → 0, the cosine similarity of gradients for InstaFlow approaches 1️⃣.0️⃣, aligning with our derivations. In contrast, Stable Diffusion gradients behave almost randomly. 📊

Check out the plots below! 👇✨

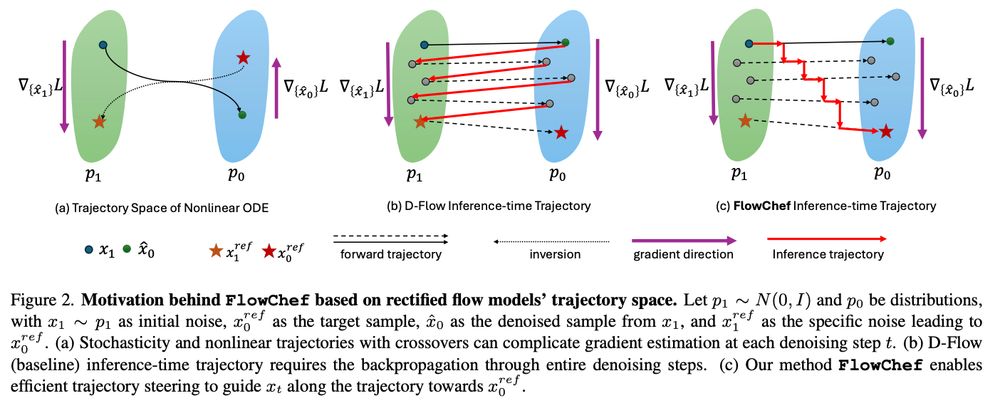
🔍 In toy settings, vector field, and cost gradients seem orthogonal, but this intuition falters in higher-dimensional ODEs (Prop. 4.1).

⚠️ Gradient-based methods need costly backpropagation in ODESolvers.

💡 We prove rectified flows skip it entirely, ensuring convergence (Lem. 4.2, Thm. 4.3). 🚀

Thanks @saxon.me!

Hi @csprofkgd.bsky.social, Could you add me as well?

Hi @gowthami.bsky.social, would appreciate it if you could add me as well.