The paper is: arxiv.org/abs/2508.11043

Finding the maximum or a minimum value of a single-variable polynomial is standard calculus fare, but doing this for polynomials of multiple variables is very hard. Our paper presents a method that works better than any other know methods for many polynomials.

If k is the size of the matrix then this quantity is exactly the rank of the matrix. If k = 1 then the matrix must be diagonal and this quantity is again the rank of the matrix. For intermediate values of k, more interesting stuff happens.

The goal of the paper is to answer the question "If a matrix can be written as a convex combination of rank-one PSD matrices that are each non-zero only on a single k-by-k principal submatrix, what is the fewer number of matrices needed in that convex combination?"

I always present this as a fun final-lecture activity in intro linear algebra to try to give students an idea of how far-reaching eigenvalues are (you can use a 91-by-91 matrix to model the sequence of lengths and then its maximal eigenvalue is that 1.3-ish limiting ratio.

I would expect that you could prove this straightforwardly from the fact that the sequence of lengths satisfies an order 72 linear recurrence relation. But the existence of that huge recurrence relation might not count as elementary.

Are those platonic solid dice soft/plushie? If so, I have the exact same set in my office! I use them to illustrate symmetries when teaching group theory :)

Paths, vector fields, scalar and vector line integrals, differentiation of vector value functions, divergence, curl, Greens theorem, and stokes theorem.

Not sure if PPT can do that. My setup is a bit convoluted: I have two instances of OBS running (one to record me and one to record my screen), and then I overlay myself and do editing in a program called Capcut.

Yep! I actually have two instances of OBS running at once - one to record me and one to record the PDF notes on my screen. Then I put it all together (and overlay the Desmos clips etc on top) in Capcut.

Shameless self-promotion time: if you enjoyed this thread and/or are interested in these sorts of aspects of Conway's Game of Life, have a look at my (free) book "Conway's Game of Life: Mathematics and Construction", co-authored with Dave Greene: www.conwaylife.com/book/

#3 (4/4) This bound has now been improved, culminating in 2024 with Keith Amling proving an upper bound of 1176/2087 ≈ 0.563. We still don't know the exact answer, but this is the first progress that was made in over 3 decades: conwaylife.com/forums/viewt...

#3 (3/4) However, it's natural to ask whether or not the same is true of infinitely large oscillators. There are plenty of infinitely large oscillators with average density equal to 0.5, but until 2023 the best known *upper* bound on the average density of an oscillator was 8/13 ≈ 0.615.

#3 (2/4) In 1999, Noam Elkies proved that this conjecture is true. That is, there is no infinitely large still life with more than half of the cells in the Life grid alive: arxiv.org/abs/math/990...

#3 (1/4): Oscillator density. In the early days of Life, it was conjectured that the maximum density (i.e., maximum ratio of alive cells to dead cells) of an infinitely large still life is 0.5. This density is easily attained by alternating rows of dead and alive cells.

#2 (4/4) In 2024, a large collaborative effort extended this to all 22-cell still lifes. To get a sense of scale, there are 672172 still lifes with 22 cells. That's 672172 different patterns to construct by colliding gliders together: conwaylife.com/forums/viewt...

#2 (3/4) For this reason, people have been cataloging glider syntheses of patterns in Life ever since the early 1970s. We've known how to synthesize all small (say 10 cell or smaller) still lifes and oscillators since those early days. Recently this was pushed to all <= 21-cell still lifes in 2022.

#2 (2/4) Glider synthesis is the key ingredient of Life that makes it possible to build most of the complex mega-patterns that you hear about. If you zoom in on a pattern like Gemini, for example, you'll see that it's almost entirely made of gliders: conwaylife.com/wiki/Gemini

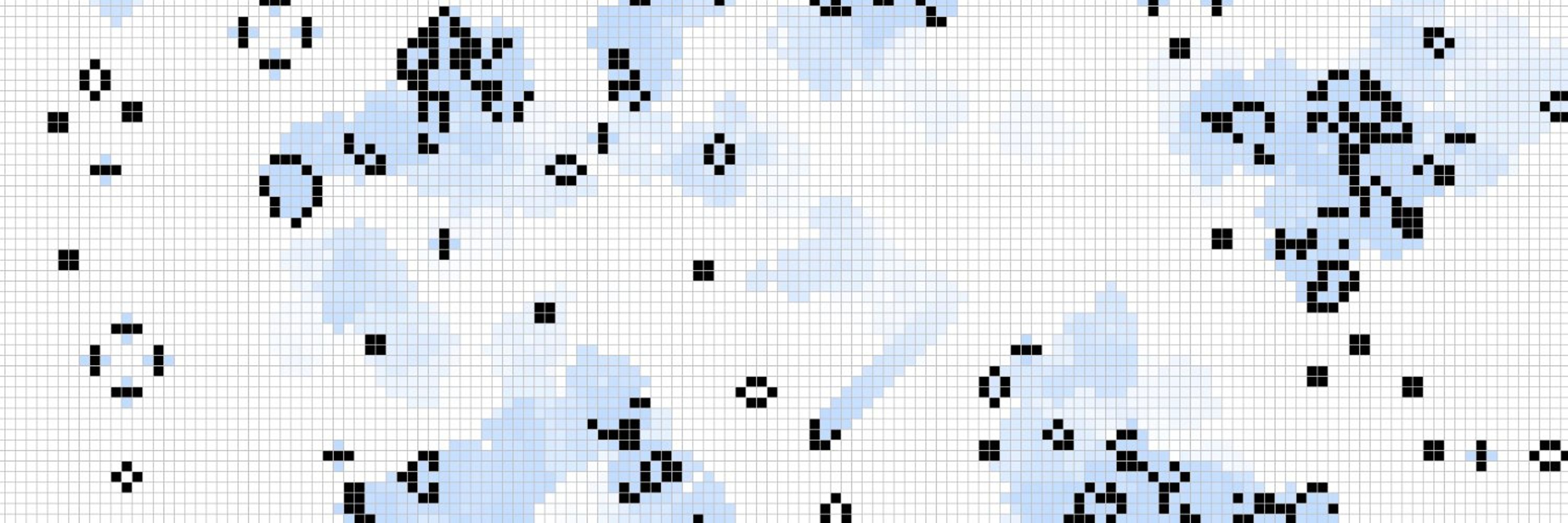
#2 (1/4): Still life glider synthesis. A glider synthesis is a way of crashing together 2 or more gliders so as to create another object. For example, in the image below three gliders collide so as to create a lightweight spaceship.