i understand that registrations are still open, with some massive discounts (and even fee waivers!) for students. hope to see many of you there!!!
5/5

i understand that registrations are still open, with some massive discounts (and even fee waivers!) for students. hope to see many of you there!!!
5/5
(hope everyone else is doing fine at #ICML2025 nevertheless!)

(hope everyone else is doing fine at #ICML2025 nevertheless!)
10/n
10/n
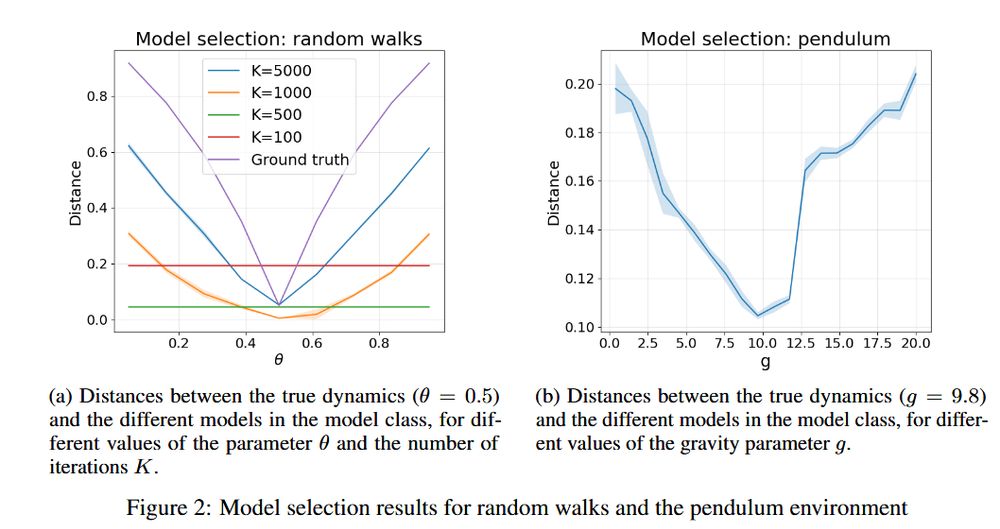
we ran some experiments to illustrate this, e.g., here we use SOMCOT to discover the latent structure of a block Markov chain without any prior knowledge
9/n
we ran some experiments to illustrate this, e.g., here we use SOMCOT to discover the latent structure of a block Markov chain without any prior knowledge
9/n
8/n

8/n
7/n

7/n
6/n


6/n
4/n

4/n
3/n

3/n
2/n
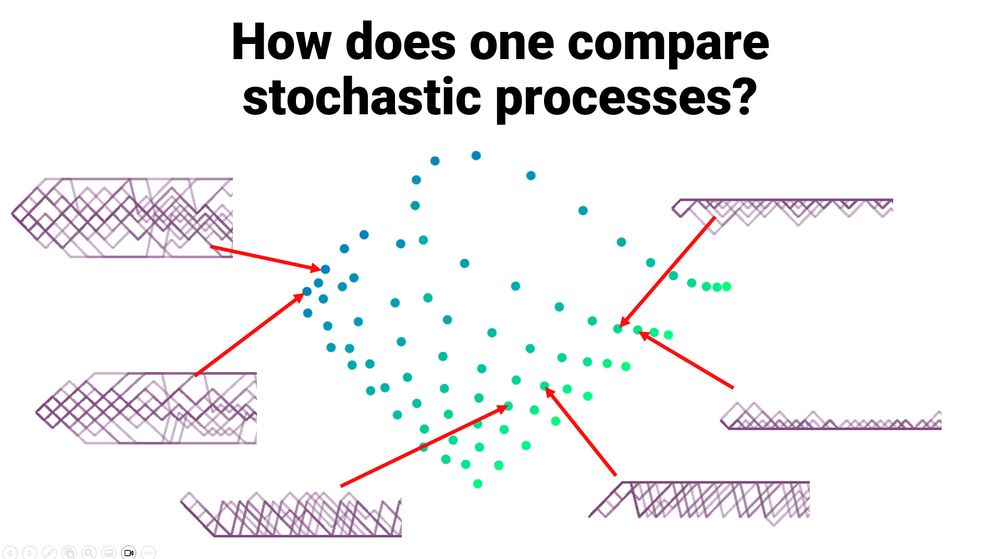
2/n
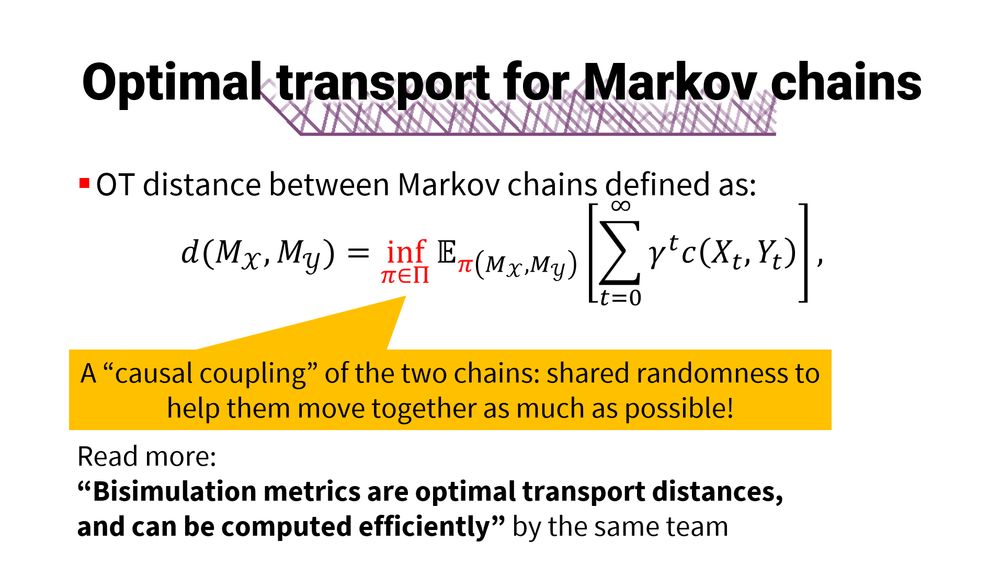
- learn distances between Markov chains
- extract "encoder-decoder" pairs for representation learning
- with sample- and computational-complexity guarantees
read on for some quick details..
1/n
- learn distances between Markov chains
- extract "encoder-decoder" pairs for representation learning
- with sample- and computational-complexity guarantees
read on for some quick details..
1/n


(from Boaz's ALT 2025 keynote)

(from Boaz's ALT 2025 keynote)
my friend Wojtek Kotlowski also helped out quite a lot.
12/

my friend Wojtek Kotlowski also helped out quite a lot.
12/
8/

8/
7/

7/
6/

6/
5/

5/
3/

3/
2/

2/
"CONFIDENCE SEQUENCES FOR GENERALIZED LINEAR MODELS VIA REGRET ANALYSIS"
TL;DR: we reduce the problem of designing tight confidence sets for statistical models to proving the existence of small regret bounds in an online prediction game
read on for a quick thread 👀👀👀
1/

"CONFIDENCE SEQUENCES FOR GENERALIZED LINEAR MODELS VIA REGRET ANALYSIS"
TL;DR: we reduce the problem of designing tight confidence sets for statistical models to proving the existence of small regret bounds in an online prediction game
read on for a quick thread 👀👀👀
1/