
Still trying to understand how things work.
https://multifario.sourceforge.io/henderson/
I might be wrong.
www.worldscientific.com/doi/10.1142/...
A very weird surface. Points on it satisfy 3d ODE with bcs and four parameters. It can be embedded in 4d, but projected into 3d it crosses itself.
The colors have to do with a classification of the solutions - # loops and twists.


www.worldscientific.com/doi/10.1142/...
A very weird surface. Points on it satisfy 3d ODE with bcs and four parameters. It can be embedded in 4d, but projected into 3d it crosses itself.
The colors have to do with a classification of the solutions - # loops and twists.
Each step picks a point on the boundary for a new disk. The boundary is a simple list.
Each step picks a point on the boundary for a new disk. The boundary is a simple list.
He doesn't like the (dU/dP)_V notation or mysticism (his word) about entropy.
But what's with the bibliography? All references are labelled 1? Later there are some 2's.




He doesn't like the (dU/dP)_V notation or mysticism (his word) about entropy.
But what's with the bibliography? All references are labelled 1? Later there are some 2's.
The phase constraint just is. We're talking about paths on the phase manifold, and not all paths are allowed? And for a path there's work done and a heat flow needed?
BTW This ⬇️isn't helping thank you.

The phase constraint just is. We're talking about paths on the phase manifold, and not all paths are allowed? And for a path there's work done and a heat flow needed?
BTW This ⬇️isn't helping thank you.
Head hurts


Head hurts

Am reading www.fys.ku.dk/~andresen/BA... and trying to get my head around work and heat flow being differential forms on the manifold of state (???!)

Am reading www.fys.ku.dk/~andresen/BA... and trying to get my head around work and heat flow being differential forms on the manifold of state (???!)
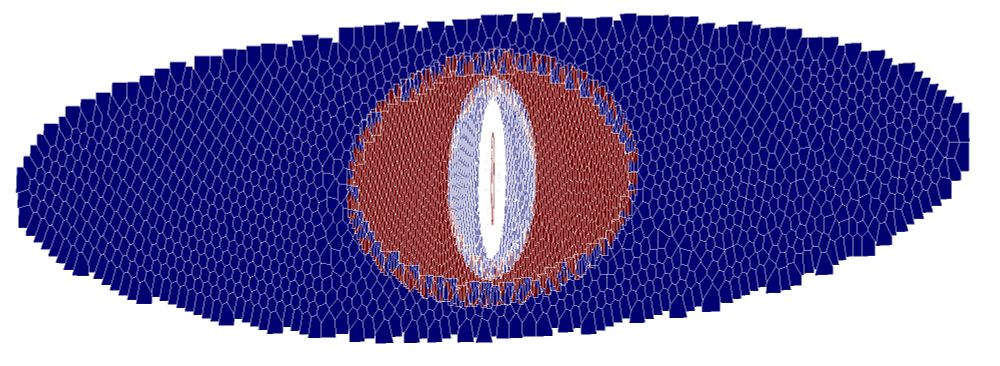
The surface is rendered as white with black polygons. Hidden line removal but still black and white.



The surface is rendered as white with black polygons. Hidden line removal but still black and white.




multifario.sourceforge.io/henderson/mu...

multifario.sourceforge.io/henderson/mu...
multifario.sourceforge.io/henderson/ve...
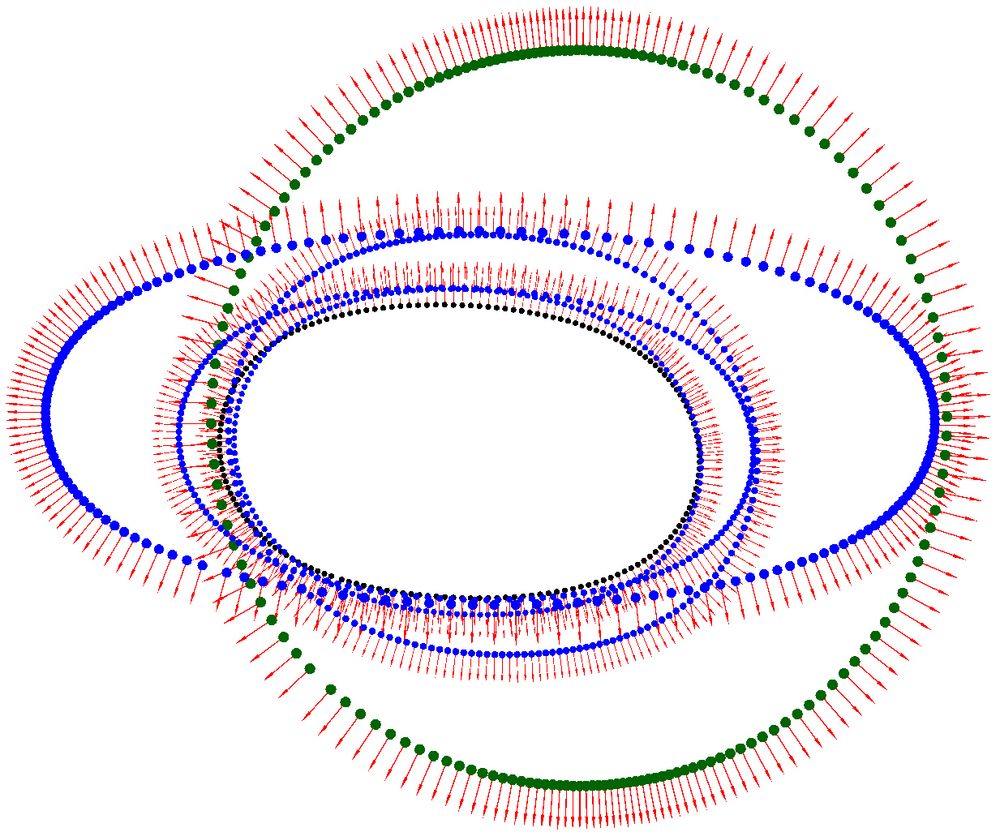
Changing each vector independently isn't the best, but it is what I set out to do. Uses a tensor product Bezier approx.
Next to find and mark the fixed points.

multifario.sourceforge.io/henderson/ve...
Changing each vector independently isn't the best, but it is what I set out to do. Uses a tensor product Bezier approx.
Next to find and mark the fixed points.







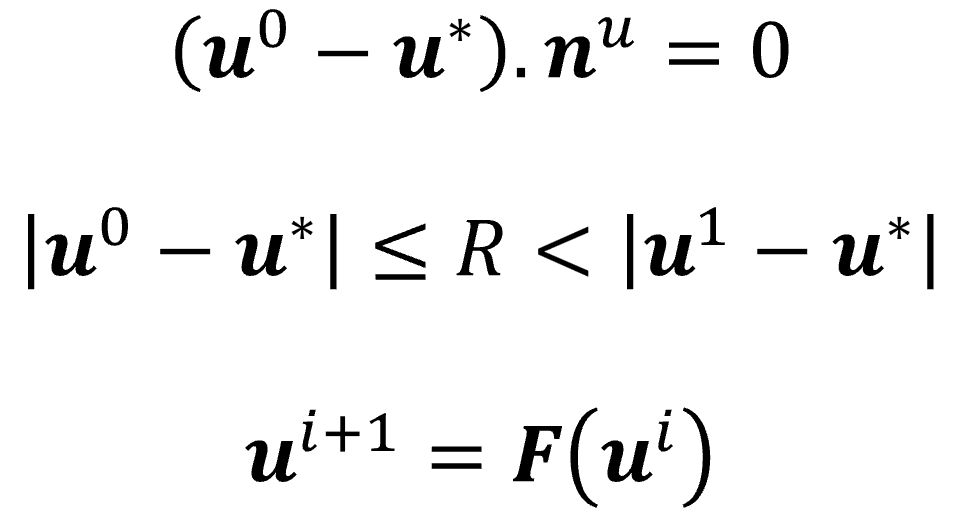


Ooo. Cool the way the reflections show on the waves.

Ooo. Cool the way the reflections show on the waves.
The curves/surfaces are points on all trajectories of a mapping (2d->2d and 3d->3d) starting on a manifold of initial conditions (a circle/sphere here).
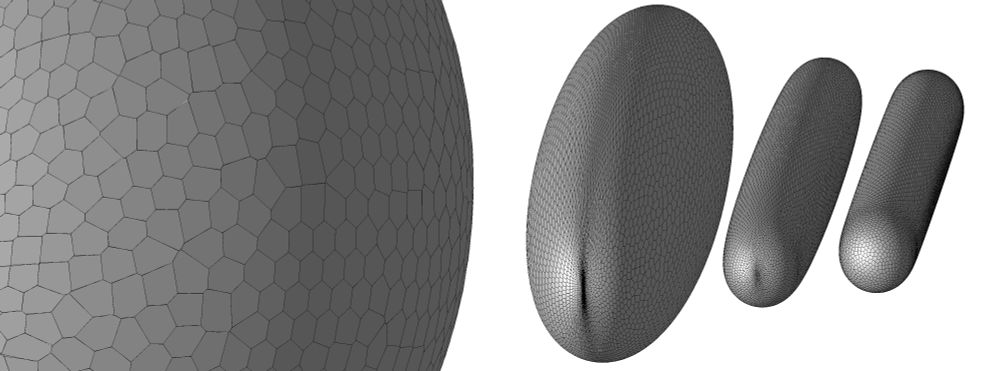
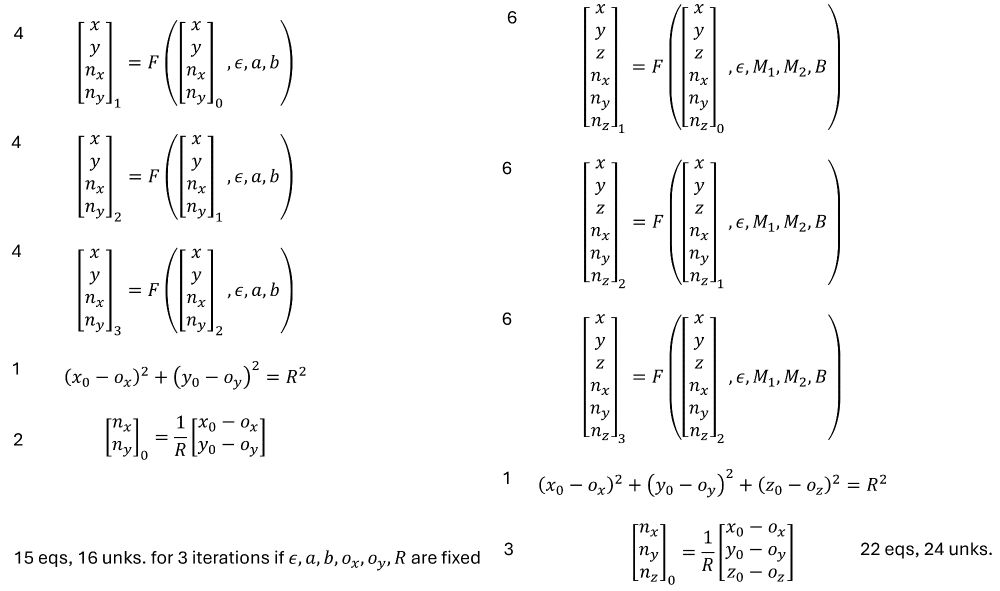
The curves/surfaces are points on all trajectories of a mapping (2d->2d and 3d->3d) starting on a manifold of initial conditions (a circle/sphere here).
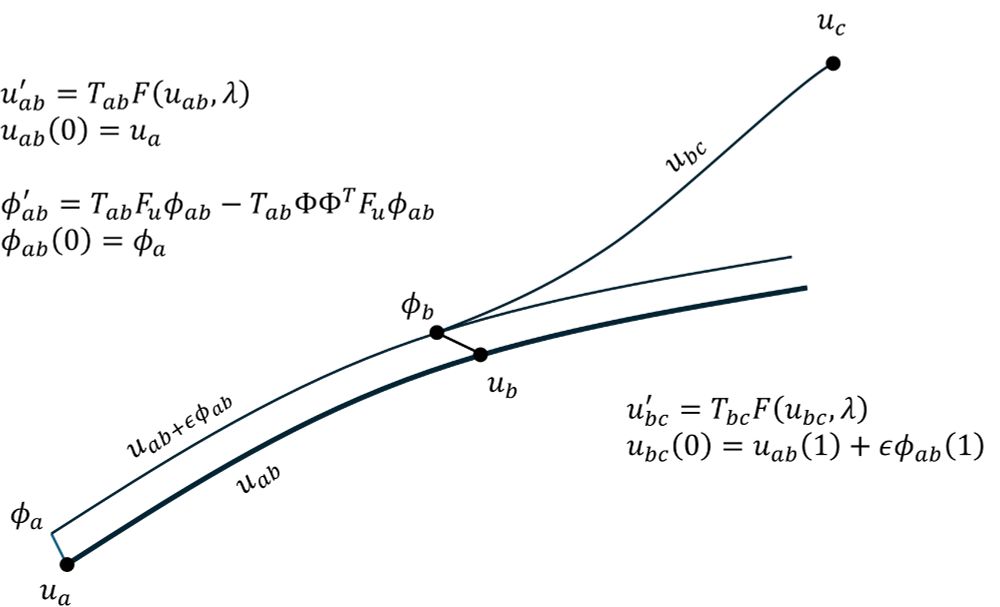
Invariant manifolds defined by smooth transverse sections are "easy". Those associated with a trajectory (like a periodic orbit) are collections of trajectories that approach or diverge from a curve tangent to the flow.
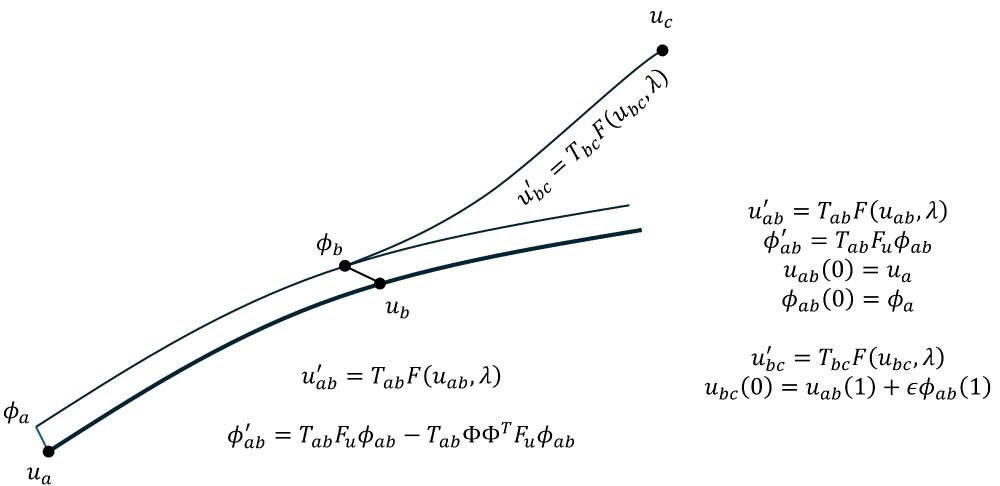
Invariant manifolds defined by smooth transverse sections are "easy". Those associated with a trajectory (like a periodic orbit) are collections of trajectories that approach or diverge from a curve tangent to the flow.

