Creator of Quibans for Core Maths. https://quibans.blogspot.com/
Based near Cambridge, UK
One of the images used to illustrate the story? The usual sort of nonsense...

One of the images used to illustrate the story? The usual sort of nonsense...


Any comments on the predictions?

Any comments on the predictions?
Scary to realise hope much time I have spent on the app.
There are 1440 mins in a day. So if I have spent a minute each day Tapping then that's more than a full day in total. (Not that this realisation will make me stop, obvs!)

Scary to realise hope much time I have spent on the app.
There are 1440 mins in a day. So if I have spent a minute each day Tapping then that's more than a full day in total. (Not that this realisation will make me stop, obvs!)
According to their figures, from 1986 to 2024 (ignoring the 2025 increase) school fees have multiplied by 9.6
(so fees of £3000 in 1986 would be 3000 x 9.6 = £28,000 in 2024).
/1
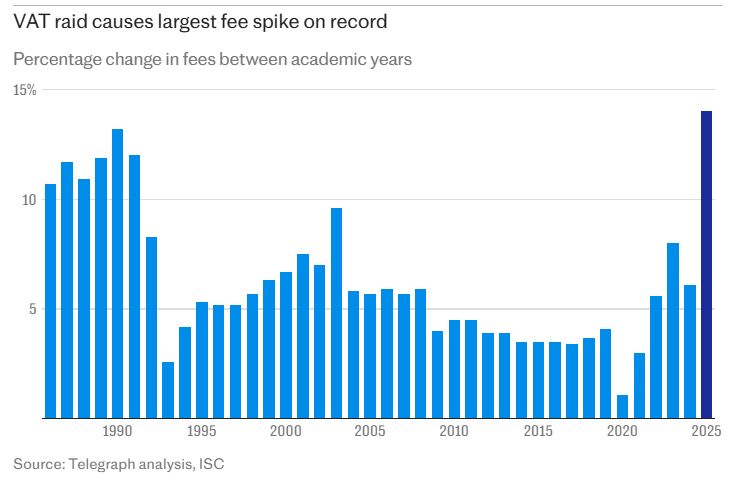
According to their figures, from 1986 to 2024 (ignoring the 2025 increase) school fees have multiplied by 9.6
(so fees of £3000 in 1986 would be 3000 x 9.6 = £28,000 in 2024).
/1
A great run in the sun!

A great run in the sun!

#MathsToday

#MathsToday
How do you manage to do the highlighted part? I get nerd-sniped. Every. Single. Time.
Can't possibly wait a week.

How do you manage to do the highlighted part? I get nerd-sniped. Every. Single. Time.
Can't possibly wait a week.

I've put some labels on the diagram.
The shaded area is equivalent to the area of the triangle ACD (which is (1/2)b(g+h) ) subtract the area of BCD ((1/2)bg)
This gives (1/2)bh as required.
Nice!

I've put some labels on the diagram.
The shaded area is equivalent to the area of the triangle ACD (which is (1/2)b(g+h) ) subtract the area of BCD ((1/2)bg)
This gives (1/2)bh as required.
Nice!
Nice floor tiles too...
Are the black tiles all the same size? If not, which are bigger?
#mathstoday

Nice floor tiles too...
Are the black tiles all the same size? If not, which are bigger?
#mathstoday
Almost no-one seems to have ever used the second one here.

Almost no-one seems to have ever used the second one here.
Have you seen the 'official' methods, in Appendix 1 of the Maths national curriculum?
assets.publishing.service.gov.uk/media/5a7c5b...
Here's the long multiplication example.

Have you seen the 'official' methods, in Appendix 1 of the Maths national curriculum?
assets.publishing.service.gov.uk/media/5a7c5b...
Here's the long multiplication example.

Brilliant organisation.
Much faster than expected too (84 min 2 sec).
Very pleased.
#EduRunners

Brilliant organisation.
Much faster than expected too (84 min 2 sec).
Very pleased.
#EduRunners



A surprisingly nice-looking solution, though!

A surprisingly nice-looking solution, though!
The area of the triangle is ½ × 2 × 2/tan(α)
The volume is therefore 12/tan(α)
/7

The area of the triangle is ½ × 2 × 2/tan(α)
The volume is therefore 12/tan(α)
/7
In this version, I did the area of the rectangle subtract the area of the triangle.
y = 3tan(α)
Blue area is 6 – ½ × 3 × 3tan(α)
Multiply by the length to get 36 – 27tan(α)
/6

In this version, I did the area of the rectangle subtract the area of the triangle.
y = 3tan(α)
Blue area is 6 – ½ × 3 × 3tan(α)
Multiply by the length to get 36 – 27tan(α)
/6
This is a brilliant problem, because it requires two cases to be considered.
/5


This is a brilliant problem, because it requires two cases to be considered.
/5
Area of isosceles triangle is ½absinC, which is ½sin(2α)
Right-hand right-angled triangle has area ½bxh, which is ½sin(α)cos(α). Area of isos triangle is twice this, giving ½sin(2α) = sin(α)cos(α) so
sin(2α) = 2sin(α)cos(α)
/4


Area of isosceles triangle is ½absinC, which is ½sin(2α)
Right-hand right-angled triangle has area ½bxh, which is ½sin(α)cos(α). Area of isos triangle is twice this, giving ½sin(2α) = sin(α)cos(α) so
sin(2α) = 2sin(α)cos(α)
/4
The area of the sector, using ½r²θ is ½(π – 2α).
The area of the triangle, using ½absinC is ½sin(π – 2α).
Sine of (π – 2α) is equal to the sine of 2α.
The area of the blue segment is therefore ½(π – 2α) – ½sin(2α)
/2

The area of the sector, using ½r²θ is ½(π – 2α).
The area of the triangle, using ½absinC is ½sin(π – 2α).
Sine of (π – 2α) is equal to the sine of 2α.
The area of the blue segment is therefore ½(π – 2α) – ½sin(2α)
/2
I decided to work in radians because it made the calculations less messy, so assumed an A-level class, but it works for a high-attaining GCSE group in degrees too.
First I needed to understand the diagram. I thought of it like the first image, and then added another line.
/1


I decided to work in radians because it made the calculations less messy, so assumed an A-level class, but it works for a high-attaining GCSE group in degrees too.
First I needed to understand the diagram. I thought of it like the first image, and then added another line.
/1

